2
where F is a family index (-1 for SA, 0 for SAB, and +1 for SB
galaxies) and T is the stage index on the RC2 numerical scale. The
formulae are applicable only to spirals in the type range 0  T
T
 8 (S0/a to Sdm; see
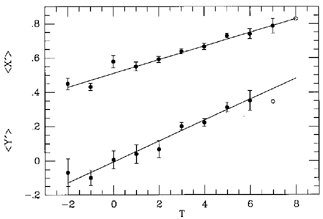
Figure 25), and they indicate that inner
rings and pseudorings are relatively larger in barred galaxies than in
nonbarred galaxies, and in earlier types than in later types. Although
relative inner ring size could thus be taken as an indicator of
apparent ``bar strength'' at a given type, or of type at a given
family, the trends shown in Figure 25 reflect
a complex mix
of possible resonance types for nonbarred or weakly barred inner rings,
differences in the mass distributions between early and late-type
galaxies, and possibly even in the nature of rings in nonbarred
galaxies (sections 15 and
17).
8 (S0/a to Sdm; see
Figure 25), and they indicate that inner
rings and pseudorings are relatively larger in barred galaxies than in
nonbarred galaxies, and in earlier types than in later types. Although
relative inner ring size could thus be taken as an indicator of
apparent ``bar strength'' at a given type, or of type at a given
family, the trends shown in Figure 25 reflect
a complex mix
of possible resonance types for nonbarred or weakly barred inner rings,
differences in the mass distributions between early and late-type
galaxies, and possibly even in the nature of rings in nonbarred
galaxies (sections 15 and
17).
Figure 25. Mean logarithmic diameter ratios
X' = log (D0 / Dr) +
0.13F and Y' = log (Ae /
Dr) + 0.13F versus stage T, from
de Vaucouleurs & Buta
(1980b).
Open circles are based on only one galaxy.
|
Absolute linear diameters Dr of inner rings and
pseudorings have been studied by
Kormendy (1979a),
Pedreros & Madore
(1981), and
Buta and de
Vaucouleurs (1982).
Kormendy focussed only on a sample of 121
bright SB galaxies, and found that the basic correlation for linear
inner ring and lens diameters is with the absolute magnitude
MoB,
and hence mass, of the parent galaxy. The correlation between
log Dr
and MoB had a slope of -5.0 within the
uncertainties, which he
concluded to mean that the mean surface brightness (as if all of the
light is concentrated within the rings) of the galaxies is independent
of luminosity. The lower mean surface brightness of later-type ringed
galaxies was attributed to a variation of mass-to-light ratio with
type, which he suggested implied that the mean mass density outside the
core region is constant for all morphological types. He concluded that
the total mass of a galaxy uniquely determines the size of a bar and
all of its associated components. Kormendy also found a correlation
between the sizes of outer rings, pseudorings, and lenses and absolute
magnitude, but did not believe that these could provide a size scale
that determines MoB , because the rings
contain so little light. He suggested that the sizes of outer rings are
fixed by the size of the bar.
De Vaucouleurs (1956)
first suggested that inner ring and pseudoring
diameters in barred spirals might be useful as extragalactic distance
indicators. He saw definite advantages to the use of such structures at
the time, because rings are defined by ridges in the light
distribution, not isophotes, and hence can be measured with better
internal and external precision than isophotal galaxy diameters
(de Vaucouleurs 1959b).
Pedreros & Madore
(1981)
and
Buta & de Vaucouleurs
(1982)
calibrated the rings as distance indicators using
distance-independent indices of absolute magnitude such as the type and
luminosity class. Both studies showed that inner rings become smaller
with advancing stage along the Hubble sequence and with fainter
luminosity class.
Using distances from the luminosity index,  c = (T +
Lc) / 10,
where T is the numerical stage (RC2 and RC3 scale) and
Lc is the inclination-corrected luminosity class (also
numerically coded;
de Vaucouleurs 1979),
and the B-band
Tully-Fisher relation
(Bottinelli et
al. 1980),
Buta & de Vaucouleurs
(1982)
derived the following formula for spirals of type Sab and
later:
c = (T +
Lc) / 10,
where T is the numerical stage (RC2 and RC3 scale) and
Lc is the inclination-corrected luminosity class (also
numerically coded;
de Vaucouleurs 1979),
and the B-band
Tully-Fisher relation
(Bottinelli et
al. 1980),
Buta & de Vaucouleurs
(1982)
derived the following formula for spirals of type Sab and
later:
log Dr (pc) = 3.61 + 0.15F - 0.10(T - 4) -
0.05(Lc - 3)
3
This shows that the largest inner rings and pseudorings are found in
early-type barred spirals of high luminosity. For an SB(r)ab I galaxy,
the ring diameter averages about 11.5 kpc. However, for the average
ringed galaxy of type SAB(r)bc II, the ring diameter is only about 4
kpc.
Pedreros & Madore
(1981)
also tried a formulation using
both type and luminosity class as separate parameters (rather than
as the combined luminosity index) and found weakly significant
differences between SB galaxies on one hand and SA+SAB galaxies on the
other. Their general formulation for a moderately unbiased sample
(SA+SAB+SB inclusive) gave the following formula for the apparent ring
diameter (in arcseconds) reduced to a radial velocity of 5000 km
s-1:
R(5000) = -2.05L - 1.31T + 29.46 4
where L is the raw numerical luminosity class (not
inclination-corrected). This study gave a greater dependence on
luminosity class than the formulation of Buta and de Vaucouleurs,
but the difference may reflect differences in the sample
characteristics and calibrating distances.
Buta & de Vaucouleurs
(1982)
also considered the sizes of rings in S0
galaxies and derived a formulation based only on the Hubble type and
family of the galaxy, since luminosity classes are not defined for
types earlier than Sab (T=2). The absolute linear diameters of inner
rings over the range -2  T
T
 7 can be derived from this
alternative formulation:
7 can be derived from this
alternative formulation:
log Dr (pc) = 3.81 + 0.15F + 0.05(T - 2.5),
-2  T
T  2
5a
2
5a
log Dr (pc) = 3.81 + 0.15F - 0.12(T -
2.5), 3  T
T  7
5b
7
5b
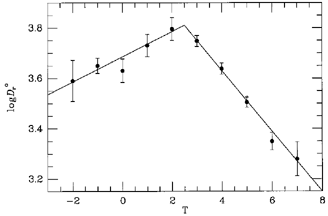
Figure 26 shows that the reduced diameter, log
Dro = log Dr - 0.15F,
of inner rings and pseudorings from these formulae achieves a maximum
of 6.1 kpc at stage Sab. A very similar trend is seen in Figure 7
of Pedreros & Madore
(1981).
Buta & Crocker (1993)
have presented information on the diameters of
inner, outer, and nuclear rings in a limited subset of galaxies which
have at least a nuclear ring or related feature. Logarithmic means
gave average diameters of 1.1, 9.5, and 22.4 kpc for nuclear, inner,
and outer rings and pseudorings, respectively, in  20 SB
galaxies. These are based on distances derived from radial velocities
and an assumed Hubble constant of 100 km s-1 Mpc-1.
The diameters of rings in weakly barred and nonbarred galaxies were
also considered, and found to show greater scatter.
20 SB
galaxies. These are based on distances derived from radial velocities
and an assumed Hubble constant of 100 km s-1 Mpc-1.
The diameters of rings in weakly barred and nonbarred galaxies were
also considered, and found to show greater scatter.
Many galaxies possess both inner and outer rings simultaneously. The
co-existence of these features in the same galaxy provides a more
dynamically interesting diameter ratio than those in equations 1 and
2. It was found by
de Vaucouleurs (1956),
Athanassoula et
al. (1982),
Kormendy (1982a),
and Buta
(1984,
1986a,
1995)
that the ratio
dR / dr (rings and pseudorings
together) has a relatively small
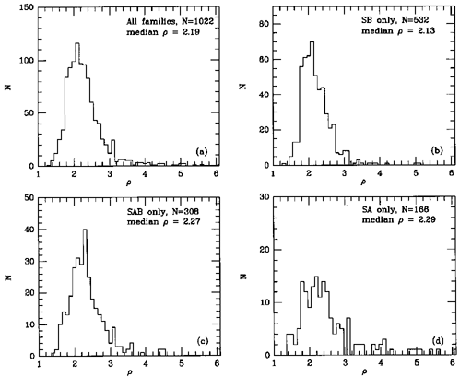
dispersion with a mean or median near 2.0. The largest samples, from
the Catalog of Southern Ringed Galaxies
(Buta 1995),
gave the
distributions in Figure 27. Since the rings are
noncircular on average (see section 9.3),
the plot shows the
distributions of ratios  of
geometric mean diameters rather
than major axis diameters. For more than 1000 galaxies of all families,
the median ratio of geometric mean ring diameters is 2.19, very similar
to the outer ring to bar diameter derived by
Kormendy (1979a).
When the
sample is divided by family, little dependence is found: 2.29 for SA,
2.27 for SAB, and 2.13 for SB galaxies. As noted by
Athanassoula et
al. (1982),
the scatter is larger for SA galaxies than for SB
galaxies.
of
geometric mean diameters rather
than major axis diameters. For more than 1000 galaxies of all families,
the median ratio of geometric mean ring diameters is 2.19, very similar
to the outer ring to bar diameter derived by
Kormendy (1979a).
When the
sample is divided by family, little dependence is found: 2.29 for SA,
2.27 for SAB, and 2.13 for SB galaxies. As noted by
Athanassoula et
al. (1982),
the scatter is larger for SA galaxies than for SB
galaxies.
Figure 27. Distributions of ratio of
geometric outer and inner ring/pseudoring diameters, from
Buta (1995).
The upper left panel is irrespective of family, while the other
panels separate barred, weakly barred, and nonbarred galaxies.
|
Buta & Crocker (1993)
have also considered ring ratios in systems with
nuclear rings. For about 20 objects with strong bars, logarithmic averages
gave ratios of 18.9, 8.7, and 2.2 for dR /
dnr , dr / dnr , and
dR / dr , respectively. No evidence
for a significant type dependence
of these ratios was found. Weakly-barred and nonbarred galaxies displayed
considerably more scatter and possible weak type dependences in the same
ratios.



 T
T
 8 (S0/a to Sdm; see
Figure 25), and they indicate that inner
rings and pseudorings are relatively larger in barred galaxies than in
nonbarred galaxies, and in earlier types than in later types. Although
relative inner ring size could thus be taken as an indicator of
apparent ``bar strength'' at a given type, or of type at a given
family, the trends shown in Figure 25 reflect
a complex mix
of possible resonance types for nonbarred or weakly barred inner rings,
differences in the mass distributions between early and late-type
galaxies, and possibly even in the nature of rings in nonbarred
galaxies (sections 15 and
17).
8 (S0/a to Sdm; see
Figure 25), and they indicate that inner
rings and pseudorings are relatively larger in barred galaxies than in
nonbarred galaxies, and in earlier types than in later types. Although
relative inner ring size could thus be taken as an indicator of
apparent ``bar strength'' at a given type, or of type at a given
family, the trends shown in Figure 25 reflect
a complex mix
of possible resonance types for nonbarred or weakly barred inner rings,
differences in the mass distributions between early and late-type
galaxies, and possibly even in the nature of rings in nonbarred
galaxies (sections 15 and
17).

 c = (T +
Lc) / 10,
where T is the numerical stage (RC2 and RC3 scale) and
Lc is the inclination-corrected luminosity class (also
numerically coded;
de Vaucouleurs 1979),
and the B-band
Tully-Fisher relation
(Bottinelli et
al. 1980),
Buta & de Vaucouleurs
(1982)
derived the following formula for spirals of type Sab and
later:
c = (T +
Lc) / 10,
where T is the numerical stage (RC2 and RC3 scale) and
Lc is the inclination-corrected luminosity class (also
numerically coded;
de Vaucouleurs 1979),
and the B-band
Tully-Fisher relation
(Bottinelli et
al. 1980),
Buta & de Vaucouleurs
(1982)
derived the following formula for spirals of type Sab and
later:
 T
T
 7 can be derived from this
alternative formulation:
7 can be derived from this
alternative formulation:
 T
T  2
2
 T
T  7
7
 20 SB
galaxies. These are based on distances derived from radial velocities
and an assumed Hubble constant of 100 km s-1 Mpc-1.
The diameters of rings in weakly barred and nonbarred galaxies were
also considered, and found to show greater scatter.
20 SB
galaxies. These are based on distances derived from radial velocities
and an assumed Hubble constant of 100 km s-1 Mpc-1.
The diameters of rings in weakly barred and nonbarred galaxies were
also considered, and found to show greater scatter.
 of
geometric mean diameters rather
than major axis diameters. For more than 1000 galaxies of all families,
the median ratio of geometric mean ring diameters is 2.19, very similar
to the outer ring to bar diameter derived by
Kormendy (1979a).
When the
sample is divided by family, little dependence is found: 2.29 for SA,
2.27 for SAB, and 2.13 for SB galaxies. As noted by
Athanassoula et
al. (1982),
the scatter is larger for SA galaxies than for SB
galaxies.
of
geometric mean diameters rather
than major axis diameters. For more than 1000 galaxies of all families,
the median ratio of geometric mean ring diameters is 2.19, very similar
to the outer ring to bar diameter derived by
Kormendy (1979a).
When the
sample is divided by family, little dependence is found: 2.29 for SA,
2.27 for SAB, and 2.13 for SB galaxies. As noted by
Athanassoula et
al. (1982),
the scatter is larger for SA galaxies than for SB
galaxies.



