


9.3. Intrinsic Shapes and Orientations
Inner and Outer Rings, Pseudorings, and Lenses
Determining the intrinsic shapes and orientations of galactic rings
with respect to bars is one of the most important means of connecting
rings to specific orbital resonances. Test-particle models
described in section 12.2 show that a
resonance can impress its ``stamp''
on the morphology of a gaseous ring which forms near it, owing to
the distinctive nature of periodic orbits in a bar potential.
Contopoulos (1979)
illustrated the properties of these orbits and
showed that alignments changed by 90° across a major resonance
and that orbits achieved their maximum local eccentricity near
a major resonance.
Schwarz (1984a)
showed that model gaseous rings
formed from slow secular evolution of bar-driven spiral structure,
and that the gas collects into the largest periodic orbit near
a resonance which does not cusp and which does not cross another
orbit. Model gaseous rings took on the oval shapes and bar alignments
of these orbits.
The intrinsic shapes and orientations of galactic rings have been
deduced from distributions of apparent axis ratios and relative
bar/ring position angles under the assumption of random orientations of
the spin axes. De Vaucouleurs
(1956; see
de Vaucouleurs & Buta
1980a)
produced the first catalogue of apparent major and minor axis
dimensions of inner and outer rings and lenses that later could be used
for this purpose
(Athanassoula et
al. 1982;
Buta 1984).
The sample included 532 galaxies of all Hubble types.
Kormendy (1979a)
measured diameters and angles for his small sample of SB galaxies, and was the
first to really attempt to deduce intrinsic shapes from such
measurements. Other sources of diameters include
Pedreros & Madore
(1981),
who measured rings in a similar-sized sample for the distance
scale, and
Corwin et al. (1985),
who provided measurements of ring diameters in a sample of 2000 southern
galaxies. The early studies of intrinsic shapes and orientations by
Kormendy (1979a),
Athanassoula et
al. (1982),
Buta (1984,
1986a),
and
Schwarz (1984c)
provided some evidence for oval intrinsic shapes and
preferred alignments, but were not very definitive because the samples
used were either too small or ill-suited to statistics, or the
observational errors were not explicitly taken into account.
The Catalog of Southern Ringed Galaxies
(Buta 1995 =
CSRG) has provided
the largest samples and the best statistics of intrinsic ring shapes
and orientations. It is based on uniform searches of the Science
Research Council (SRC) IIIa-J Southern Sky Survey, which is the highest
quality of all of the available sky surveys. The J filter-plate match
has an effective wavelength between Johnson B and V
filters but is closer to B than V, thus making the plates
ideal for detecting the typically blue rings
(see section
9.4). Other advantages of the SRC-J
survey for ringed galaxy studies are the fine grain of the emulsion,
which counters the small image scale and allows rings as small as
0'.2 to be resolved well enough to measure at least
axis ratios; and the depth of exposure of the plates, which is
sufficient to reveal rings which are as faint as 1% of the night sky
brightness. The principal disadvantage of the J plates is the frequent
overexposure of galaxy core regions, but ESO-B and ESO-R films usually
provided the necessary information in such cases.
Together, the three southern sky surveys have provided a very large
database of apparent ring diameters, axis ratios, relative bar/ring
position angles, and morphologies. The CSRG
includes 3,692 galaxies and information on 4661 ring, pseudoring, and
lens features. We illustrate in Figures 28, 29,
30 three sets of distributions from
Buta (1995),
where the filled circles refer to the CSRG data, and
summarize in Table 7 the best current estimates
of the intrinsic shapes
and orientations derived under the assumption of random orientations of
the spin axes (solid histograms). The principal result from these kinds
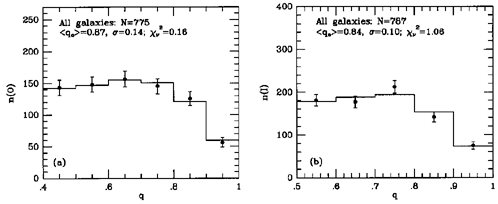
of studies is that rings in galaxies are, in general, noncircular on
average. The distributions in Figure 28 are
for inner and outer rings, pseudorings, and lenses irrespective of
family. In the analysis of
Buta (1995),
rings and lenses were not treated as distinct
features. Selection effects in the observed distributions are discussed by
Buta (1995),
the main effect being inclination. For the
best model fits, which allow for observational error, both inner and
outer features have an average intrinsic axis ratio of  0.85
with a dispersion of
0.85
with a dispersion of  0.1. When the samples are subdivided by
family or feature subtype as in Table 7, some
possibly significant
differences are found. For example, both inner and outer rings,
pseudorings, and lenses in SA galaxies may be rounder on average than
those in SB galaxies. Inner rings and ring/lenses seem to be more oval
on average than inner pseudorings, while outer rings and ring/lenses
may be slightly less oval than outer pseudorings. SAB inner and outer
features have characteristics that are not necessarily intermediate
between those for SA and SB features.
0.1. When the samples are subdivided by
family or feature subtype as in Table 7, some
possibly significant
differences are found. For example, both inner and outer rings,
pseudorings, and lenses in SA galaxies may be rounder on average than
those in SB galaxies. Inner rings and ring/lenses seem to be more oval
on average than inner pseudorings, while outer rings and ring/lenses
may be slightly less oval than outer pseudorings. SAB inner and outer
features have characteristics that are not necessarily intermediate
between those for SA and SB features.
Figure 28. Model fits to observed axis
ratio (q) distributions for outer ring, pseudoring, and lens
features (left) and inner ring, pseudoring, and lens features (right),
irrespective of family, from
Buta (1995).
The  2 per degree of freedom
is indicated.
2 per degree of freedom
is indicated.
|
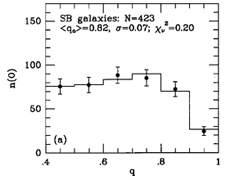
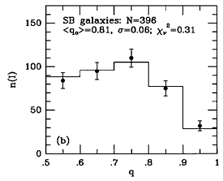
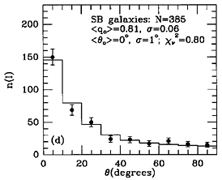
Figure 29. Model fits to observed axis
ratio (q) and bar/ring position angle ( ) distributions for outer
(left) and inner (right) rings, pseudorings, and lenses in SB
galaxies, from
Buta (1995).
) distributions for outer
(left) and inner (right) rings, pseudorings, and lenses in SB
galaxies, from
Buta (1995).
| 
|
| 
|
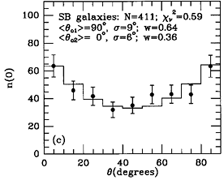
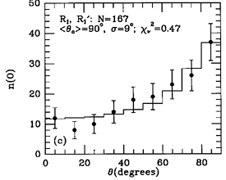
Figure 30. Model fits to observed axis
ratio (q) and bar/ring position angle ( ) distributions for
R1, R'1 and R2, R'2 outer
features (known as the OLR subclasses), from
Buta (1995).
) distributions for
R1, R'1 and R2, R'2 outer
features (known as the OLR subclasses), from
Buta (1995).

| 
|
| 
|
The shape results for outer rings in Table 7 can
be compared with
statistics of isophotal disk shapes, since outer rings are
preferentially located in the outer regions of a disk.
Fasano et al. (1993)
have used a volume-limited sample of 1064 RC3 galaxies to deduce
that early-type spiral galaxies have a more triaxial disk than
late-types. The distribution of intrinsic shapes, inferred by
inversion
(Lucy 1974),
gave a peak at planar axis ratio
b/a = 0.8,
comparable to SB outer rings and pseudorings. However, the ring and
disk samples are very different in nature, and the significance of
the agreement in intrinsic shapes is unclear.
The distribution of relative bar/ring position angles is very
interesting from these kinds of studies. The distributions are inconsistent
with random alignments between bars and rings (see Figure 10 of
Buta 1986a).
As shown in Figure 29, SB inner and
outer features have about
the same distribution of apparent axis ratios, and hence about the same
average intrinsic shape, but the angle distributions are very
different. The distribution of angles for outer features can be modeled
with two populations of features having perpendicular and parallel
alignments relative to the bar. The two maxima in this distribution
favor that 64% of SB outer rings are aligned perpendicular to the bar and
36% are aligned parallel to the bar. The distribution of angles for
inner rings favors parallel alignment exclusively.
Figure 30 shows that
the two maxima in the angle distribution for SB outer features are
connected to the ``OLR'' subclasses, R'1 and R'2.
The latter are found to be rounder on average than the former, and
their perpendicular relative alignments are strikingly illustrated. For
SAB galaxies, the same two alignments are probably present, but in a
greatly different proportion: 85% parallel-aligned, and 15%
perpendicular-aligned.
The statistics described above give a very good indication of the
properties of the average ring, but do not tell us the extremes
possible for any given features.
Buta (1986a),
in a preliminary study
of the CSRG data available at the time, deduced that inner rings in SB
galaxies have a wide range of intrinsic axis ratios: from 0.6 to 0.95.
Among low-inclination barred galaxies, extremely oval inner rings are
found in NGC 1433 (Figure
3), NGC 6782 (Figure
76), IC 1438 (Figure
9), ESO 296-2, and
ESO 325-28 (Figure 17), while nearly circular inner rings are
found in NGC 53, 6761, and 7329
(Figure 43). The
differences are not obviously connected to apparent bar strength (i.e.,
SB versus SAB).
TABLE VII. Intrinsic Shapes and Alignments of
Galaxy Rings
| Feature
| < q0 > ±  ( q0 ) ( q0 )
| <  0 >
± 0 >
±  ( (  0 ) 0 )
| N
|
| inner features, all families
| 0.84 ± 0.10
| -
| 787
|
| SB inner features
| 0.81 ± 0.06
| 0° ± 1°
| 396
|
| SB(r,rl) only
| 0.78 ± 0.04
| 0° ± 3°
| 251
|
| SB(rs) only
| 0.88 ± 0.04
| 0° ± 1°
| 122
|
| SAB inner features
| 0.78 ± 0.14
| 0° ± 8°
| 215
|
| SA inner features
| 0.92 ± 0.09
| -
| 172
|
|
|
| outer features, all families
| 0.87 ± 0.14
| -
| 775
|
| R1, R'1
| 0.74 ± 0.08
| 90° ± 9°
| 187
|
| R2, R'2
| 0.87 ± 0.06
| 0° ± 6°
| 135
|
| SB outer features
| 0.82 ± 0.07
| 0° ± 6° (36%)
90° ± 9° (64%)
| 423
|
| (R,RL)SB only
| 0.84 ± 0.04
| 0° ± 6° (26%)
90° ± 9° (74%)
| 152
|
| (R')SB only
| 0.80 ± 0.11
| 0° ± 6° (42%)
90° ± 9° (58%)
| 262
|
| SAB outer features
| 0.94 ± 0.16
| 0° ± 6° (85%)
90° ± 9° (15%)
| 208
|
| SA outer features
| 0.97 ± 0.21
| -
| 138
|
Nuclear Rings and Pseudorings
The intrinsic shapes and orientations of nuclear rings and their
pseudoring counterparts cannot be obtained at the same level of
precision as for inner and outer features. The reason is that most
nuclear features are too small or overexposed to detect on sky survey
material, and as a consequence it is currently not possible to build up
the large samples required to make a definitive analysis. Less than
100 examples are currently known in galaxies ranging in type from S0 to Sc.
Buta & Crocker (1993)
have used low-inclination galaxies to
deduce that nuclear rings range in intrinsic axis ratio from
 0.7 to
0.7 to  1.0. If oval, they are
generally misaligned
with the main bar at an intermediate angle between 0°
to 90°, although cases of exactly parallel (NGC 4314)
or perpendicular (NGC 1317) alignments are known.
1.0. If oval, they are
generally misaligned
with the main bar at an intermediate angle between 0°
to 90°, although cases of exactly parallel (NGC 4314)
or perpendicular (NGC 1317) alignments are known.



 0.85
with a dispersion of
0.85
with a dispersion of  0.1. When the samples are subdivided by
family or feature subtype as in Table 7, some
possibly significant
differences are found. For example, both inner and outer rings,
pseudorings, and lenses in SA galaxies may be rounder on average than
those in SB galaxies. Inner rings and ring/lenses seem to be more oval
on average than inner pseudorings, while outer rings and ring/lenses
may be slightly less oval than outer pseudorings. SAB inner and outer
features have characteristics that are not necessarily intermediate
between those for SA and SB features.
0.1. When the samples are subdivided by
family or feature subtype as in Table 7, some
possibly significant
differences are found. For example, both inner and outer rings,
pseudorings, and lenses in SA galaxies may be rounder on average than
those in SB galaxies. Inner rings and ring/lenses seem to be more oval
on average than inner pseudorings, while outer rings and ring/lenses
may be slightly less oval than outer pseudorings. SAB inner and outer
features have characteristics that are not necessarily intermediate
between those for SA and SB features.



 2 per degree of freedom
is indicated.
2 per degree of freedom
is indicated.

 ) distributions for outer
(left) and inner (right) rings, pseudorings, and lenses in SB
galaxies, from
) distributions for outer
(left) and inner (right) rings, pseudorings, and lenses in SB
galaxies, from








 ( q0 )
( q0 )
 0.7 to
0.7 to