© CAMBRIDGE UNIVERSITY PRESS 1999

11. PECULIAR MOTIONS OF CLUSTERS

How is the mass distributed in the universe? Does it follow, on the average, the light distribution? To address this important question, peculiar motions on large scales are studied in order to directly trace the mass distribution. It is believed that the peculiar motions (motions relative to a pure Hubble expansion) are caused by the growth of cosmic structures due to gravity. A comparison of the mass-density distribution, as reconstructed from peculiar velocity data, with the light distribution (i.e., galaxies) provides information on how well the mass traces light (see chapter by Dekel, 1994). The basic underlying relation between peculiar velocity and density is given by

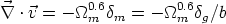
(58)

where _m ( / )_m is the mass overdensity, _g is the galaxy overdensity, and b _g / _m is the bias parameter discussed in Section 6. A formal analysis yields a measure of the parameter _m^0.6/b. Other methods that place constraints on include the anisotropy in the galaxy distribution in the redshift direction due to peculiar motions (see Strauss and Willick 1995 for a review).

Measuring peculiar motions is difficult. The motions are usually inferred with the aid of measured distances to galaxies or clusters that are obtained using some (moderately-reliable) distance-indicators (such as the Tully-Fisher or D_n - relations), and the measured galaxy redshift. The peculiar velocity v_p is then determined from the difference between the measured redshift velocity, cz, and the measured Hubble velocity, v_H, of the system (the latter obtained from the distance-indicator): v_p = cz - v_H.

A summary of all measurements of made so far is presented in Strauss and Willick (1995). The dispersion in the current measurements of is very large; the various determinations range from ~ 0.4 to ~ 1, implying, for b 1, _m ~ 0.2 to ~ 1. No strong conclusion can therefore be reached at present regarding the values of or _m. The larger and more accurate surveys currently underway, including high precision velocity measurements, will likely lead to the determination of and possibly its decomposition into _m and b (e.g., Cole et al. 1994).

Clusters of galaxies can also serve as efficient tracers of the large-scale peculiar velocity field in the universe (Bahcall, Gramann and Cen 1994). Measurements of cluster peculiar velocities are likely to be more accurate than measurements of individual galaxies, since cluster distances can be determined by averaging a large number of cluster members as well as by using different distance indicators. Using large-scale cosmological simulations, Bahcall et al. 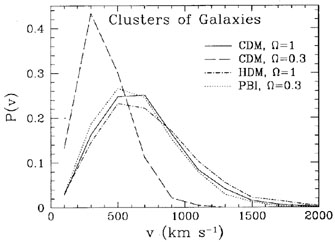(1994) find that clusters move reasonably fast in all the cosmological models studied, tracing well the underlying matter velocity field on large scales. The clusters exhibit a Maxwellian distribution of peculiar velocities as expected from Gaussian initial density fluctuations. The model cluster 3-D velocity distribution, presented in Figure 10, typically peaks at v ~ 600 km s^-1 and extends to high cluster velocities of ~ 2000 km s^-1. The low-density CDM model exhibits lower velocities (Fig. 10). 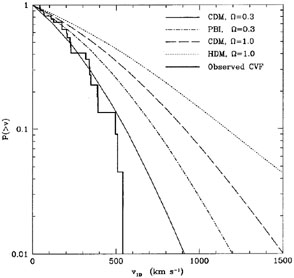Approximately 10% of all model rich clusters (1% for low-density CDM) move with v 10³ km s^-1. A comparison of model expectation with recent, well calibrated cluster velocity data (Giovanelli et al. 1996) is presented in Figure 11 (Bahcall and Oh 1996). The comparison between models and observations suggests that the cluster velocity data is consistent with a low-density CDM model, and is inconsistent with a standard _m = 1 CDM model, since no high velocity clusters are observed.

Figure 10. Differential three-dimensional peculiar velocity distribution of rich clusters of galaxies for four cosmological models (Bahcall, Gramann and Cen 1994).

Figure 11. Observed vs. model cluster peculiar velocity functions (from Bahcall and Oh 1996). The Giovanelli and Haynes (1996) data are compared with model expectations convolved with the observational errors. Note the absence of a high velocity tail in the observed cluster velocity function.

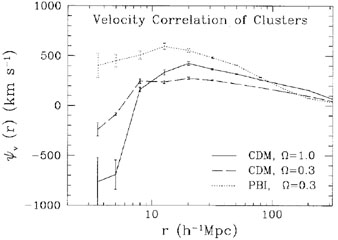
Cen, Bahcall and Gramann (1994) determined the expected velocity correlation function of clusters in different cosmologies. They find that close cluster pairs, with separations r 10h^-1 Mpc, exhibit strong attractive motions; the pairwise velocities depend sensitively on the model. The mean pairwise attractive cluster velocities on 5h^-1 Mpc scale ranges from ~ 1700 km s^-1 for _m = 1 CDM to ~ 700 km s^-1 for _m = 0.3 CDM. The cluster velocity correlation function, presented in Figure 12, is negative on small scales--indicating large attractive velocities, and is positive on large scales, to ~ 200h^-1 Mpc - indicating significant bulk motions in the models. None of the models reproduce the very large bulk flow of clusters on 150h^-1 Mpc scale, v 689 ± 178 km s^-1, recently reported by Lauer and Postman (1994). The bulk flow expected on this large scale is generally 200 km s^-1 for all the models studied (_m = 1 and _m 0.3 CDM, and PBI).

Figure 12. Velocity correlation function of rich (R 1) clusters of galaxies for three models. Error bars indicate the 1 statistical uncertainties (from Cen et al. 1994).