© CAMBRIDGE UNIVERSITY PRESS 1999

10. The Cluster Correlation Function

The correlation function of clusters of galaxies efficiently quantifies the large-scale structure of the universe. Clusters are correlated in space more strongly than are individual galaxies, by an order of magnitude, and their correlation extends to considerably larger scales (~ 50h^-1 Mpc). The cluster correlation strength increases with richness ( luminosity or mass) of the system from single galaxies to the richest clusters (Bahcall and Soneira 1983; Bahcall and West 1992). The correlation strength also increases with the mean spatial separation of the clusters (Szalay and Schramm 1985; Bahcall and Burgett 1986; Bahcall and West 1992). This dependence results in a "universal" dimensionless cluster correlation function; the cluster dimensionless correlation scale is constant for all clusters when normalized by the mean cluster separation.

Empirically, two general relations have been found (Bahcall and West 1992) for the correlation function of clusters of galaxies, _i = A_ir^-1.8:

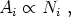
	(56)
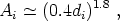
	(57)

where A_i is the amplitude of the cluster correlation function, N_i is the richness of the galaxy clusters of type i (Section 2.2), and d_i is the mean separation of the clusters. Here d_i = n_i^-1/3, where n_i is the mean spatial number density of clusters of richness N_i (Section 2.3) in a volume-limited, richness-limited complete sample. The first relation, Eq. (56), states that the amplitude of the cluster correlation function increases with cluster richness, i.e., rich clusters are more strongly correlated than poorer clusters. The second relation, Eq. (57), states that the amplitude of the cluster correlation function depends on the mean separation of clusters (or, equivalently, on their number density); the rarer, large mean separation richer clusters are more strongly correlated than the more numerous poorer clusters. Eqs. (56) and (57) relate to each other through the richness function of clusters, i.e., the number density of clusters as a function of their richness. Equation (57) describes a universal scale-invariant (dimensionless) correlation function with a correlation scale r_{o, i} = A_i^1/1.8 0.4d_i (for 30 d_i 90h^-1 Mpc).

There are some conflicting statements in the literature about the precise values of the correlation amplitude, A_i. Nearly all these contradictions are caused by not taking account of Eq. (56). When apples are compared to oranges, or the clustering of rich clusters is compared to the clustering of poorer clusters, differences are expected and observed.

Figure 6 clarifies the observational situation. The A_i(d_i) relation for groups and clusters of various richnesses is presented in the figure. The recent automated cluster surveys of APM (Dalton et al. 1992) and EDCC (Nichol et al. 1992) are consistent with the predictions of Eqs. (56) and (57), as is the correlation function of X-ray selected ROSAT clusters of galaxies (Romer et al. 1994). Bahcall and Cen (1994) show that a flux-limited sample of X-ray selected clusters will exhibit a correlation scale that is smaller than that of a volume-limited, richness-limited sample of comparable apparent spatial density since the flux-limited sample contains poor groups nearby and only the richest clusters farther away. Using the richness-dependent cluster correlations of Eqs. (56) and (57), Bahcall and Cen (1994) find excellent agreement with the observed flux-limited X-ray cluster correlations of Romer et al. (1994).

Figure 6. The universal dimensionless cluster correlations: the dependence of correlation amplitude on mean separation (Bahcall and West 1992). Data points include different samples and catalogs of clusters and groups, as well as X-ray-selected and cD clusters. Quasars and radio galaxies, as represented by their parent groups, are also included. The APM results are presented; they are consistent with the expected relation.

The strong correlation amplitude of galaxy clusters, and the large scales to which clusters are observed to be positively correlated ( ~ 50-100h^-1 Mpc), complement and quantify the superclustering of galaxy clusters discussed in Section 9. Clusters of galaxies are strongly clustered in superclusters of large scales (Section 9), consistent with the strong cluster correlations to these scales (Section 10).

This fundamental observed property of clusters of galaxies - the cluster correlation function - can be used to place strong constraints on cosmological models and the density parameter _m by comparison with model expectations. Bahcall and Cen (1992) contrasted these cluster observations with standard and nonstandard CDM models using large N-body simulations (400h^-1 box, 10^7.2 particles). They find that none of the standard _m = 1 CDM models can fit consistently the strong cluster correlations. A low-density (_m ~ 0.2-0.3) CDM-type model (with or without a cosmological constant), however, provides a good fit to the cluster correlations (see Figs. 7-9) as well as to the observed cluster mass-function (Section 7, Fig. 5). This is the first CDM-type model that is consistent with the high amplitude and large extent of the correlation function of the Abell, APM, and EDCC clusters. Such low-density models are also consistent with other observables as discussed in this paper. The _m constraints of these cluster results are model dependent; a mixed hot + cold dark matter model, for example, with _m = 1, is also consistent with these cluster data (see Primack's chapter in this book).

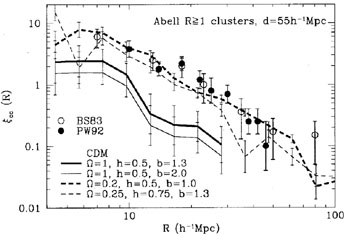
The CDM results for clusters corresponding to the rich Abell clusters (richness class R 1) with d = 55h^-1 Mpc are presented in Figure 7 together with the observed correlations (Bahcall and Soneira 1983; Peacock and West 1992). The results indicate that the standard _m = 1 CDM models are inconsistent with the observations; they cannot provide either the strong amplitude or the large scales ( 50h^-1 Mpc) to which the cluster correlations are observed. Similar results are found for the APM and EDCC clusters.

Figure 7. Two-point correlation function of Abell R 1 clusters, with mean separation 55h-1 Mpc, from observations and the CDM simulations (Bahcall and Cen 1992).

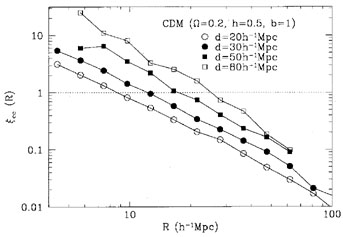
Figure 8. Model dependence of the cluster correlation function on mean separation d (CDM simulation: = 0.2, h = 0.5, b = 1) (from Bahcall and Cen 1992).

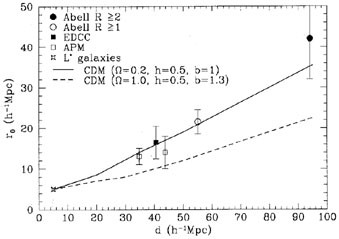
Figure 9. Correlation length as a function of cluster separation, from both observations and simulations (Bahcall and Cen 1992).

The dependence of the observed cluster correlation on d was also tested in the simulations. The results are shown in Figure 8 for the low-density model. The dependence of correlation amplitude on mean separation is clearly seen in the simulations. To compare this result directly with observations, I plot in Figure 9 the dependence of the correlation scale, r_o, on d for both the simulations and the observations. The low-density model agrees well with the observations, yielding r₀ 0.4d, as observed. The _m = 1 model, while also showing an increase of r_o with d, yields considerably smaller correlation scales and a much slower increase of r₀(d ).

What causes the observed dependence on cluster richness [Eqs. (56-57]? The dependence, seen both in the observations and in the simulations, is most likely caused by the statistics of rare peak events, which Kaiser (1984) suggested as an explanation of the observed strong increase of correlation amplitude from galaxies to rich clusters. The correlation function of rare peaks in a Gaussian field increases with their selection threshold. Since more massive clusters correspond to a higher threshold, implying rarer events and thus larger mean separation, Eq. (57) results. A fractal distribution of galaxies and clusters would also produce Eq. (57) (e.g., Szalay and Schramm 1985).