4. COMPONENTS OF THE NIGHT SKY SPECTRUM

The spectrum of the night sky from Earth includes integrated starlight (ISL), zodiacal light (ZL), EBL, and diffuse Galactic light (DGL) from above the atmosphere, as well as atmospheric emission, or airglow. Light from all sources is scattered by molecules and particulates in the atmosphere, causing considerable redirection from one line of sight to another. Absorption by particulates is a minor effect compared to the scattering by both components. The net effect of atmospheric scattering on a source with small angular extent (e.g. stars and galaxies) is atmospheric "extinction." The net scattering out of the line of sight can be measured in the typical way using standard stars, as in Section 3.6. Light from a very extended source (e.g. ZL, ISL) will not suffer the same "extinction"; rather, it will appear to be smoothed out over the sky as light from different regions scatters into and out of the line of sight. The efficiency of scattering in the atmosphere is conveniently described in the familiar way as the extinction along the line of sight _obs().

If the scattering angles were small, and the diffuse, extended source were uniform over the sky, then the scattering into and out of the line of sight would roughly cancel. However, Rayleigh scattering occurs over very broad angles and the relative surface brightness of ZL and ISL changes strongly over the sky. We must therefore explicitly calculate the net effects of scattering in our observing situation (determined by the observatory location and positions of the Sun, Galaxy, and target), as they are not intuitive. This is done in detail in the Appendix. We summarize the results here.

We can describe the observed spectrum of the night sky in the target field, I_NS, as follows:

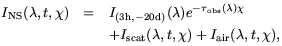
(3)

in which I_{(3h, -20d)}() is the flux from the target field (coordinates = 3.00h, = - 20.18d), _obs() is the extinction for a point source, is the airmass of the target field at the time of observations, I_scat(, t,) is the light scattered into the line of sight as a function of time and wavelength, and I_air(, t,) is the effective airglow along the line of sight (including any scattering effects which redistribute airglow over the sky). The flux from the target field, I_{(3h, -20d)}(), includes the EBL, DGL and ZL flux within the solid angle of the slit. There is no ISL component coming directly from the target field because the slit simply contains no stars to V = 24 mag. The slit also provides an extremely effective pupil stop which prevents contributions from discrete sources off-axis. ⁽¹⁾ I_scat(, t,) can be expressed as

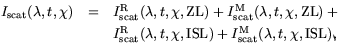
(4)

where the superscript R or M denotes Rayleigh scattering (due to molecules) or Mie scattering (due to particulates), the parenthetical ZL or ISL denotes the source being scattered, and the parenthetical , t, and denote dependence on those variables. We do not include the DGL in Equation 4 explicitly because the total DGL is at least a factor of 50 times fainter than the direct ISL and is therefore a trivial component (< 0.2% at 2<UT<6.5) of the scattered light. The EBL is not included as it does not have strong spectral features (see Section 5).

At any altitude, Rayliegh scattering is the dominant effect. Because the particulate density is concentrated at low altitudes, this is especially true at high altitude observatories. The total extinction, as measured for a point source, is equal to the sum of the molecular and particulate extinction, _obs() = _M() + _R(). Rayleigh extinction, _R, can be calculated from the well-known density distribution of the atmosphere for any observatory. Mie extinction, which varies with time and geography, can be inferred from the difference between the observed and Rayleigh extinction. At LCO, the extinction due to Mie scattering is 20-40% of the Rayleigh extinction.

We have calculated the scattered light from all terms in Equation 4 in the Appendix at 30 minute intervals throughout the nights of our observations. To briefly summarize the results of our calculations, the ZL total flux scattered into the line of sight (gained) at any time during our observations is less than the total flux scattered out of the line of sight (lost). Thus, the net result of atmospheric scattering for the case of ZL in our situation is still a net extinction of order 2-8%, which we can conveniently describe by an effective extinction, _eff, which we use in place of _obs for ZL (see Figures A10 and A11 in the Appendix). We can check the scattering predictions of our calculations in our ZL analysis itself by looking for changes in the ZL solution with time. We estimate that our calculation of the scattered ZL has an average uncertainty of 8%, which translates into a systematic uncertainty in our ZL measurement of 1.2%.

In the case of the ISL, the total flux gained due to scattering into the line of sight is 12-24% of the total ZL flux from low to high airmass. However, the crucial issue is not the total mean flux, but rather the strength of the spectral features which are in common with the Sun (see Figure A15 in the Appendix). The net influence of the scattered ISL on observations is to increase the strength of the Fraunhofer lines over the night by 0.6 - 4% redward of 4100Å, and 5-35% blueward. Because the effect is a strong function of wavelength, it is straightforward to identify inconsistencies between the predicted ISL flux and our observations by looking for changes in the ZL solution with wavelength. We estimate that our calculation of the scattered ISL has an uncertainty of 13%, which translates into a systematic uncertainty in our ZL measurement of 0.5% over the majority of our wavelength range.

¹ No stars with V < 12 mag are within 12 arcmin of the slit, and no stars with V < 7 are within 1.5 degrees. We have carefully characterized the scattered light properties of the duPont telescope by positioning a V = 4 mag star around the field from on-axis to 20 arcmin off-axis in 4 directions at 1 arcmin intervals. The stray light entering the slit from discrete off-axis sources is more than 10^-6 fainter than surface brightness of the ZL in the field. See Paper I for further discussion. Back.