


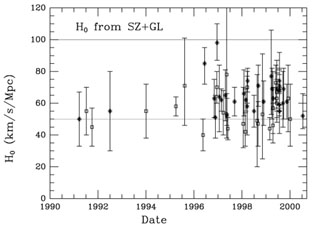
A detailed discussion of other methods is beyond the scope of this paper; however, we briefly compare our results with two other methods: the Sunyaev-Zel'dovich (SZ) technique, and measurement of time delays for gravitational lenses. Both of these methods are entirely independent of the local extragalactic distance scale, and they can be applied directly at large distances. Currently their accuracies are not yet as high as has recently been achieved for the classical distance measurements, but both methods hold considerable promise for the future. We show in Figure 7 values of H0 published based on these two methods from 1991 to the present.
|
Figure 7. Values of the Hubble constant determined using the Sunyaev-Zel'dovich effect (open squares) and gravitational lens time delays (asterisks) from 1990 to the present. From the compilation of Huchra (http://cfa-www.harvard.edu/~huchra) for the Key Project. |
9.1. The Sunyaev-Zel'dovich Effect
For clusters of galaxies, the combination of a measurement of the microwave background decrement (the SZ effect), the X-ray flux, and an assumption of spherical symmetry, yield a measurement of the distance to the cluster (e.g., Birkinshaw 1999; Carlstrom et al. 2000). The observed microwave decrement (or more precisely, the shift of photons to higher frequencies) results as low-energy cosmic microwave background photons are scattered off the hot X-ray gas in clusters. The SZ effect is independent of distance, whereas the X-ray flux of the cluster is distance-dependent: the combination thus can yield a measure of the distance.
There are also, however, a number of astrophysical complications in the practical application of this method (e.g., Birkinshaw 1999; Carlstrom 2000). For example, the gas distribution in clusters is not entirely uniform: clumping of the gas, if significant, would result in a decrease in the value of H0. There may also be projection effects: if the clusters observed are prolate and seen end on, the true H0 could be larger than inferred from spherical models. (In a flux-limited sample, prolate clusters could be selected on the basis of brightness.) Cooling flows may also be problematic. Furthermore, this method assumes hydrostatic equilibrium, and a model for the gas and electron densities. In addition, it is vital to eliminate potential contamination from other sources. The systematic errors incurred from all of these effects are difficult to quantify.
Published values of H0 based on the SZ method have ranged from ~ 40 - 80 km/sec/Mpc (e.g., Birkinshaw 1999). The most recent two-dimensional interferometry SZ data for well-observed clusters yield H0 = 60 ± 10 km/sec/Mpc. The systematic uncertainties are still large, but the near-term prospects for this method are improving rapidly (Carlstrom 2000) as additional clusters are being observed, and higher-resolution X-ray and SZ data are becoming available (e.g., Reese et al. 2000; Grego et al. 2000).
9.2. Time Delays for Gravitional Lenses
A second method for measuring H0 at very large distances, independent of the need for any local calibration, comes from gravitational lenses. Refsdal (1964, 1966) showed that a measurement of the time delay, and the angular separation for gravitationally lensed images of a variable object, such as a quasar, can be used to provide a measurement of H0 (e.g., see also the review by Blandford & Narayan 1992). Difficulties with this method stem from the fact that the underlying (luminous or dark) mass distributions of the lensing galaxies are not independently known. Furthermore, the lensing galaxies may be sitting in more complicated group or cluster potentials. A degeneracy exists between the mass distribution of the lens and the value of H0 (Schechter et al. 1997; Romanowsky & Kochanek 1999; Bernstein & Fischer 1999). In the case of the well-studied lens 0957+561, the degeneracy due to the surrounding cluster can be broken with the addition of weak lensing constraints. However, a careful analysis by Bernstein & Fischer emphasizes the remaining uncertainties in the mass models for both the galaxy and the cluster which dominate the overall errors in this kind of analysis. H0 values based on this technique appear to be converging to about 65 km/sec/Mpc (Impey et al. 1998; Franx & Tonry 1999; Bernstein & Fischer 1999; Koopmans & Fassnacht 1999; Williams & Saha 2000).
9.3. Comparison with Other Methods
It is encouraging that to within the uncertainties, there is broad
agreement in H0 values for completely independent techniques. A
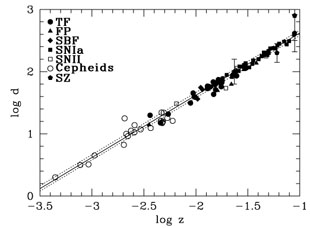
Hubble diagram (log d versus log v) is plotted in
Figure 8. This Hubble diagram covers over 3
orders of
magnitude, and includes distances obtained locally from Cepheids, from
5 secondary methods, and for 4 clusters with recent Sunyaev-Zel'dovich
measurements out to z ~ 0.1. At z
 0.1, other
cosmological parameters (the matter density,
0.1, other
cosmological parameters (the matter density,
 m, and the
cosmological constant,
m, and the
cosmological constant,

 ) become important.
) become important.
|
Figure 8. Logarithm of distance in Mpc versus logarithm of redshift for Cepheids, the Tully-Fisher relation, type Ia supernovae, surface brightness fluctuations, fundamental plane, and type II supernovae, calibrated as part of the Key Project. Solid black circles are from Birkinshaw (1999), for nearby Sunyaev-Zel'dovich clusters with cz < 30,000 (z < 0.1) km/sec, where the choice of cosmological model does not have a significant effect on the results. The SZ clusters are Abell 478, 2142, and 2256, and are listed in Birkinshaw's Table 7. The solid line is for H0 = 72 km s-1 Mpc-1, with the dashed lines representing ±10%. |