3.2. Higher Order Correlation Functions

Since the two point function alone does not describe the large scale structure, the idea is that the higher functions may fill in the gap. The three- and four- point functions have been extensively discussed and measurements of these functions has given rise to the idea that all high order correlation functions are sums of multiples of the two point function. The three point function for example (Peebles and Groth, 1975; LSSU) can be written as

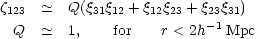
(49)

In this notation 1,2,3 denote the positions of the members of triples of galaxies. (123) is to be thought of as a function of triangles of various specific kinds specified by the lengths of their sides (12), (23), (31). Then the scaling of can be verified for all similar triangles of a given type, specified only by their size. Or it can be verified for all triangles in which two sides are the same as a function of the length of the third side.

It is worth noting the absence of a term proportional to _{12 23 31}. The argument is that this term would dominate as r 0 and we do not see that happening on the scales where the three point function has been determined.

The 3-point function plays a role in the Cosmic Virial Theorem which relates the mean square peculiar velocity <v₂₁²(r)> on scale r to the clustering as measured by the 3-point function (LSSU section 75, Peebles (1980)):

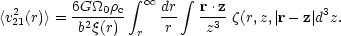
(50)

This uses the (unverified) assumption that the distribution of v₂₁ is isotropic. The bias parameter b comes in because the Cosmic Virial Theorem involves the correlation functions of the mass distribution, and these are estimated from the distribution of light. Using a model for the 2-point function

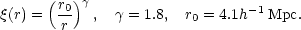
and the relation between the 3-point and 2-point functions, we get

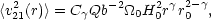
(51)

where C is a constant depending on . In this equation, the only unknown quantity is ₀.

Q has been determined for the Durham/AAT/SAAO redshift surveys (Hale-Sutton et al., 1989) to have the value

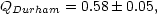
(52)

from data on scales r < 1 Mpc. This is somewhat lower than the value Q = 1.3 ± 0.2 from the analysis of projected data by Groth and Peebles (1977). With this value of Q and the velocity dispersions measured from their survey they find

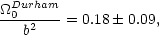
(53)

again using fits for r < 1 Mpc. The error bar seems somewhat conservative since the variation of ₀ determinations from the subsamples that make up the Durham/AAT/SAAO survey is quite considerable. The value is nonetheless on the low side if one is aiming at ₀ = 1. The value only reflects the clustered mass on scales < 1 Mpc., and there is some freedom in choosing the bias parameter.

Coles and Jones (1991) point out that Q may not be the best quantity to measure departures from Gaussian behaviour, particularly on scales where correlations are weak. They suggest instead the direct measure of the skewness:

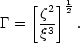
(54)

For a Gaussian random distribution of galaxies, will be zero. In general, will depend on scale and the shape of triangles used to measure .

Even higher order correlation functions can be used to measure the clustering (Sharp, Bonometto and Lucchin, 1984), but despite clever tricks they are difficult to measure (Szapudi, Szalay, and Bascan, 1991) and lack any intuitive appeal. (See also Jones and Coles (1991) for more comments on the 4-point correlation function and its relationship to the kurtosis of the underlying distribution).