3.3. Counts in cells

The counts of galaxies in cells are related to the correlation functions of all orders and potentially provide an important means of testing for the presence of voids in a sample of galaxies. The relationship between the probability P_N(V) of finding N galaxies in a sample volume V and the correlation functions of all orders was given by White (1979). The particular case P₀(V) is called the Void Probability Function, `VPF' for short, and is thought to be a sensitive discriminator of clustering models.

The probability that a volume V, randomly selected in a sample of points having mean number density n₀, will contain no galaxies was first given by White (1979)

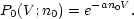
(55)

P₀ depends on the mean density of the sample, and in fact it can only depend on the product n₀V. The scale a is given in terms of the correlation functions of the distribution:

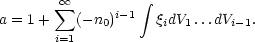
(56)

Here _i is the i-point correlation function of (i - 1) coordinates and is determined on linear scales by (among other things) the power spectrum of the primordial density fluctuations. For purely Gaussian fluctuations the sum in a is cut off beyond the second term, but as we discussed in the section on correlation function, gravitational evolution destroys the Gaussian character of fluctuations. If we wish to compute P₀(V) in a general case we are forced to make an ansatz about the relationship between second and higher order correlation functions either through BBGKY hierarchies or by intelligent guesswork (Schaeffer, 1985; Fry 1986). The data can then be used to test this hypothesis. The VPF was first studied observationally by Maurogordato and Lachieze-Rey (1987) who were able to confirm the Schaeffer scaling relations. The recent article by Einasto et al. (1991) provides a clear exposition of what the Void probability function actually measures. Cappi, Maurogodato and Lachieze-Rey (1991) have confirmed that the VPF of the distribution of rich galaxy clusters shows scaling behaviour up to a scale of 50 h^-1 Mpc.

P₀(V; n₀) should be distinguished carefully from the probability of finding a void of the kind that has been identified as a feature of the large scale galaxy surveys. The VPF describes the probability that a randomly placed sphere of a given volume V contains a given number of galaxies - not the probability of finding a region of volume V which is devoid of galaxies.

The probability of finding N galaxies in a randomly selected volume V, P_N(V) has been discussed in terms of quite general scaling hypotheses by Balian and Schaeffer (1989a, b). Balian and Schaeffer were able to compute the properties of the counts-in-cells distribution P_N(V) on the hypothesis that the higher order correlation functions are related to the two-point correlation function through rather general scaling hierarchies. The CfA survey data appears to support both the form of P_N(V) and the Balian-Schaeffer scaling hypothesis (Maurogordato and Lachieze-Rey, 1987; Alimi, Blanchard and Schaeffer, 1990). There is an extensive analysis of galaxy counts in cells by Fry et al. (1989).

An alternative approach to the counts in cells distribution was taken by Saslaw and Hamilton (1984) who argued that

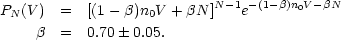
(57)

The value of the constant (called b by Saslaw and Hamilton, but we wish to avoid confusion with the bias parameter) is from Crane and Saslaw's (1986) analysis of the Zwicky catalogue of galaxies. The parameter is interpreted physically by Saslaw and Hamilton as being the ratio = - W / 2K of the gravitational correlation energy, W, to the kinetic energy in peculiar motions, K. In fact, could depend on scale and will certainly depend on time. This distribution function is discussed at length in Itoh et al. (1990a, b).

What is interesting is that this distribution function fits N-body models rather well (Suto, Itoh and Inagaki 1988, 1990), provided that depends on scale as 1 - (r) r^{- (3 - )/2}, = 1.8 being the slope of the two-point correlation function. Itoh (1990) has an interesting discussion of the relationship between the Saslaw-Hamilton distribution function and the fractal dimensions D_q of a set having this distribution function, though he somehow ends up with a set whose Hausdorff dimension D₀ is smaller than the correlation dimension D₂.