MOND - A Pedagogical Review

6. MOND AS MODIFIED GRAVITY

An implementation of MOND as a non-relativistic modified gravity was discussed by [Bekenstein & Milgrom (1984)], who replaced the standard Poisson action S in eq. (3) by an action of the form

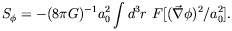
(4)

This gives, upon variation on phi , the equation

(5)

where µ(x) ident dF(y) / dy|_y=x². This theory, since it is derived from an action that has all the usual symmetries, satisfies all the standard conservation laws. Its various implications have been discussed in [Bekenstein & Milgrom (1984)], [Milgrom (1986)], [Milgrom (1997)], and others.

One important point to note is that this theory gives the desired center-of-mass motion of composite systems: Stars, star clusters, etc. moving in a galaxy with a low center-of-mass acceleration are made of constituents whose internal accelerations are much higher than 0. If we look at individual constituents we see bodies whose total accelerations are high and so whose overall motion is very nearly Newtonian. Yet, their motion should somehow combine to give a MOND motion for the center of mass. This is satisfied in the above theory as shown in [Bekenstein & Milgrom (1984)]. (A similar situation exists in GR: imagine a system made of very tightly bound black holes moving in the weak field of a galaxy, say. While the motions of the individual components is highly relativistic, governed by a non-linear theory, we know that these motions combine to give a simple Newtonian motion for the center of mass.)

This field equation, generically, requires numerical solution, but it is straightforward to solve in cases of high symmetry (spherical, cylindrical, or planar symmetry), where the application of the Gauss law to eq. (5) gives the exact algebraic relation between the MOND ( $\vec{g}\,$ = - $\vec{\nabla}\,$ phi ) and Newtonian ( $\vec{g}_{N}^{}$ = - $\vec{\nabla}\,$ phi _N) acceleration fields:

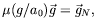
(6)

which is identical to the heuristic MOND relation we started with. Note that in general, for configurations of lower symmetry, this algebraic relation does not hold (and, in general, $\vec{g}\,$ and $\vec{g}_{N}^{}$ are not even parallel).

It is worth pointing out that in such a modified-gravity theory, the deep-MOND limit corresponds to a theory that is conformally invariant, as discussed in [Milgrom (1997)]. Whether this has some fundamental bearings is not clear, but it does make MOND unique, and enables one to derive useful analytic results, such as an expression for the two-body force, and a virial relation, despite the obstacle of nonlinearity.

There is a large number of physical phenomena that are governed by an equation like eq. (5), each with its own form of the function µ(x), as detailed in [Milgrom (1997)], or [Milgrom (2001)]. I would like to concentrate here on one, in particular. It is well known that a stationary, potential flow is described by the Poisson equation: If the velocity field $\vec{u}\,$ ( $\vec{r}\,$ ) is derived from a potential, $\vec{u}\,$ = $\vec{\nabla}\,$ phi , then the continuity equation, which here determines the flow, reads $\vec{\nabla}\,$ ^. 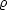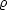$\vec{\nabla}\,$ phi = s( $\vec{r}\,$ ) / varrho ₀, where s( $\vec{r}\,$ ) is the source density, and varrho ₀ is the (constant) density of the fluid. When the fluid is compressible, but still irrotational, and barotropic [i.e. has an equation of state of the form p = p( rho )] the stationary flow is described by the nonlinear Poisson equation. The Euler equation reduces to Bernoulli's law

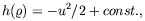
(7)

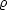where dh / d rho ident rho ^-1 dp / d rho . This tell us that varrho is a function of u = | $\vec{\nabla}\,$ phi |. Substituting this in the continuity equation gives

(8)

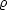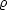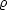which has the same form as eq. (5) if we identify varrho as µ, and the source density s with the normalized gravitational mass density 4 G rho . Note, however, that from the Bernoulli law, d varrho / d| u| = - varrho | u|/c², where c² = dp / d varrho is the formal squared speed of sound. Thus, in the case of MOND, where we have that µ is an increasing function of its argument, the model fluid has to have a negative compressibility c² < 0. 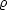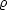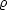A cosmological-constant equation of state, p = - c² varrho , with c the speed of light gives varrho (u) = varrho ₀ exp(u² / 2c²), which is not what we need for MOND. 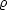The deep-MOND limit, µ(u) approx u / a₀, corresponds to p = - (a₀²/3) varrho ³. 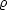To get the Newtonian limit at large values of u the equation of state has to become incompressible at some finite density varrho ₀, so that eq. (8) goes to the Poisson equation.

The gravitational force is then the pressure+drage force on sources. For a small (test) static source s, at a position where the fluid speed is $\vec{u}\,$ , the source imparts momentum to the flow at a rate s $\vec{u}\,$ , and so is subject to a force - s $\vec{u}\,$ . The force between sources of the same sign is attractive, as befits gravity.

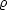Note that in such a picture the fluid density itself varrho does not contribute to the sources of the potential equation, so it does not, itself, gravitate. Also note that, because rho = p = 0 for $\vec{u}\,$ = 0, the fluid behaves as if it has no existence without the sources (masses) that induce velocities in it. Obviously, this picture is anything but directly applicable as an explanation of Newtonian gravity. For example, it is not clear how to obtain the barotropic equation of state that is needed to reproduce MOND. In particular, how does the infinite compressibility appear at a finite critical density, and what is the meaning of this density? Is this due to some phase transition? What happens at densities higher than this critical density? are they accessible at all? Also, there seem to be a drag force on moving sources. In the context of a time-dependent configuration the above equation of state is problematic.