7. MOND AS MODIFIED INERTIA

Most people seem to prefer modifying gravity to modifying inertia; perhaps because the latter seems to be less drastic; perhaps because it is a game that has been much played before. I personally feel, without concrete evidence, that there is more potential in modified inertia as the basis for MOND.

Remember first that Newtonian inertia has not been immune to changes. A familiar modification of Newtonian inertia, which is taken to be "nature given", is that brought about by Special Relativity. The single-particle kinetic action in eq. (3) is replaced by - mc² dt [1 - (v/c)²]^1/2, which gives an equation of motion

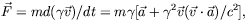
(9)

where is the Lorentz factor.

And, physics is replete with instances of modified, acquired, or effective inertia. Electrons and holes in solids can sometimes be described as having a greatly modified mass tensor. Mass renormalization and the Higgs mechanism, modify particle masses and/or endow them with mass: an effective, approximate description that encapsules the effects of interactions of the particles, with vacuum fields in the former instance, and with the Higgs field in the latter. The effects of a fluid on a body embedded in it may sometimes be described as a contribution to to the mass tensor of the body, because its motion induces motion in the fluid which carries energy and momentum. So, modified inertia might also well lie in the basis of MOND.

As a first stage of looking for Mondified inertia it might behoove us to study non relativistic modifications of inertia that incorporate the basic principle of MOND. We seek to modify the particle kinetic action S_k in eq. (3) into an action of the form S_k[(t), a₀], which is a functional of the particle trajectory (t) and depends also on one constant, a₀. It should satisfy the following asymptotic requirements: In the formal limit a₀ 0 - corresponding to all acceleration measures in the system being much larger than the actual value of a₀ (this is similar to obtaining the classical limit of quantum mechanics by taking the formal limit 0) - it should go into the standard Newtonian action. If we want to retain the MOND phenomenology, according to which in the deep MOND limit G and 0 appear only through their product Ga₀, then, in the limit a₀ , S_k a₀^-1. This can be seen by rescaling into / G in eq. (3) (and deviding the action by G).

The theory should also satisfy the more subtle requirement of the correct center-of-mass motion discuss in the previous section.

General properties of such theories are discussed in detail in [Milgrom (1994)]. Here I summarize, very succinctly, some of the main conclusions.

If the particle free action enjoys the usual symmetries: translational, rotational, and Galilei invariance, than to satisfy the two limits in 0 it must be non-local. This means that the action cannot be written as L dt, where L is a function of a finite number of derivatives of (t). This might look like a disadvantage, but, in fact, it is a blessing. A local action for MOND would have had to be a higher-derivative theory, and, as such, it would have suffered from the several severe problems that beset such theories. A non-local theory need not suffer from these. Indeed, I have discussed examples that are free of these problems. A non-local action is also a more natural candidate for an effective theory.

While nonlocal theories tend to be rather unwieldy, they do lend themselves to a straightforward treatment of the important issue of rotation curves. This is done via a virial relation that physical, bound trajectories can be shown to satisfy:

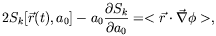
(10)

where is the (unmodified) potential in which the particle is moving, < > marks the time average over the trajectory, and S_k is the value of the action calculated for the particular trajectory (S_k is normalized to have dimensions of velocity square). In the Newtonian case this reduces to the usual virial relation. Applying this relation to circular orbits in an axi-symmetric potential, and noting that, on dimensional grounds, on such orbits with radius r and velocity v we must have S_k(r, v, a₀) = v²µ(v² / ra₀), we end up with the expression for the velocity curve

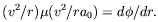
(11)

Thus the algebraic relation that was first used in MOND as a naive application of eq. (2), and which all existing rotation-curve analyzes use, is exact in modified-inertia MOND. In modified gravity this expression is a only good approximation.

Another important difference between the two interpretations is worth noting. Unlike (non-relativistic) modified gravity, where the gravitational field is modified, but in it all bodies at the same position undergo the same acceleration, in modified inertia the acceleration depends not only on position, but also on the trajectory. In the case of SR the acceleration depends on the velocity as well, but in more general theories it might depend on other properties of the orbit. There is still a generalized momentum whose rate of change is a function of position only (m in SR) but this rate is not the acceleration. This larger freedom in modified inertia comes about because we implement the modification via a modification of the action as a functional of the trajectory; namely, a function of an infinite number of variables; so, different trajectories might suffer different modifications. In modifying gravity we modify one function of the three coordinates (the gravitational potential). This is an obvious point, but is worth making because in interpreting data we equate observed accelerations with the gravitational field. While this is still true in modified gravity it is not so in modified inertia.

We can exemplify this point by considering the claimed anomaly in the motions of the Pioneer 10 and 11 spacecraft. Analysis of their motion have shown an unexplained effect (see [Anderson & al 2001]) that can be interpreted as being due to an unexplained constant acceleration towards the sun of about 7 ^. 10^-8cm s^-2, of the order of a₀. This might well be due to some systematic error, and not to new physics. This suspicion is strengthened by the fact that an addition of a constant acceleration of the above magnitude to the solar gravitational field is inconsistent with the observed planetary motions (e.g. it gives a much too large rate of planetary perihelion precession).

MOND could naturally explain such an anomalous acceleration: We are dealing here with the strongly Newtonian limit of MOND, for which we would have to know the behavior of the extrapolating function µ(x) at x > > > 1, where µ 1. We cannot learn about this from galaxy dynamics, so we just parameterize µ in this region: µ 1 - x^-n. (This is not the most general form; e.g. µ may approach 1 non analytically in x^-1, for example as 1 - exp(- x).) Be that as it may, if n = 1 we get just the desired effect in MOND: the acceleration in the field of the sun becomes M Gr^-2 + a₀ in the sun's direction. As I said above, in a modified gravity interpretation this would conflict with the observed planetary motions; but, in the modified-inertia approach it is not necessarily so. It may well be that the modification enters the Pioneers motion, which corresponds to unbound, hyperbolic motions, and the motion of bound, and quasi-circular trajectories in a different way. For example, the effective µ functions that correspond to these two motions might have different asymptotic powers n.