"Systematic effects" is a general category which includes
effects such as background, selection bias, scanning efficiency,
energy resolution, angle resolution, variation of counter
efficiency with beam position and energy, dead time, etc. The
uncertainty in the estimation of such a systematic effect is
called a "systematic error". Often such systematic effects and
their errors are estimated by separate experiments designed for
that specific purpose. In general, the maximum-likelihood
method can be used in such an experiment to determine the
systematic effect and its error. Then the systematic effect
and its error are folded into the distribution function of
the main experiment. Ideally, the two experiments can be
treated as one joint experiment with an added parameter
M+1
to account for the systematic effect.
In some cases a systematic effect cannot be estimated apart from the main experiment. Example 2 can be made into such a case. Let us assume that among the beam of mono-energetic particles there is an unknown background of particles uniformly distributed in range. In this case the distribution function would be
|
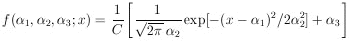
where
|
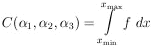
The solution
3* is simply
related to the percentage of background.
The systematic error is obtained using Eq. 11.