14. GENERALIZED MAXIMUM-LIKELIHOOD METHOD

So far we have always worked with the standard maximum-likelihood formalism, whereby the distribution functions are always normalized to unity. Fermi has pointed out that the normalization requirement is not necessary so long as the basic principle is observed: namely, that if one correctly writes down the probability of getting his experimental result, then this likelihood function gives the relative probabilities of the parameters in question. The only requirement is that the probability of getting a particular result be correctly written. We shall now consider the general case in which the probability of getting an event in dx is F(x)dx, and

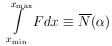
is the average number of events one would get if the same experiment were repeated many times. According to Eq. (19), the probability of getting no events in a small finite interval x is

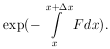
The probability of getting no events in the entire interval x_min < x < x_max is the product of such exponentials or

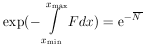
The element of probability for a particular experimental result of N events at x = x₁, ... , x_N is then

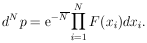
Thus we have

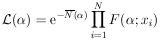
and

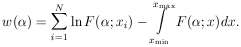
The solutions _i = _i* are still given by the M simultaneous equations:

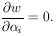
The errors are still given by

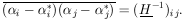
where

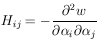
The only change is that N no longer appears explicitly in the formula

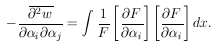
A derivation similar to that used for Eq. (8) shows that N is already taken care of in the integration over F(x).

In a private communication, George Backus has proven, using direct probability, that the Maximum-Likelihood Theorem also holds for this generalized maximum-likelihood method and that in the limit of large N there is no method of estimation that is more accurate. Also see Sect. 9.8 of Ref. 6.

In the absence of the generalized maximum-likelihood method our procedure would have been to normalize F(; x) to unity by using

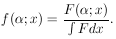
For example, consider the sample containing just two radioactive species, of lifetimes ₁ and ₂. Let ₃ and ₄ be the two initial decay rates. Then we have

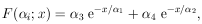
where x is the time. The standard method would then be to use

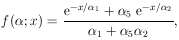
which is normalized to one. Note that the four original parameters have been reduced to three by using _{5 4} / ₃. Then ₃ and ₄ would be found by using the auxiliary equation

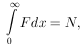
the total number of counts. In this standard procedure the equation

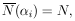
must always hold. However, in the generalized maximum-likelihood method these two quantities are not necessarily equal. Thus the generalized maximum-likelihood method will give a different solution for the _i, which should, in principle, be better.

Another example is that the best value for a cross section is not obtained by the usual procedure of setting L = N (the number of events in a path length L). The fact that one has additional prior information such as the shape of the angular distribution enables one to do a somewhat better job of calculating the cross section.