APPENDIX II: DISTRIBUTION OF THE LEAST-SQUARES SUM

We shall define the vector Z_i y_i / _i and the matrix F_ij f_j(x_i) / _i.

Note that H = F^{T .} F by Eq. (27),

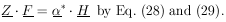
(33)

Then

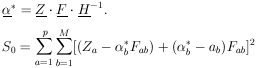
(34)

where the unstarred is used for ₀.

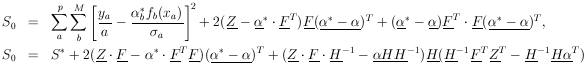
using Eq. (34). The second term on the right is zero because of Eq. (33).

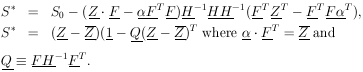
(34)

Note that

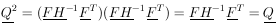
If q_i is an eigenvalue of Q, it must be equal q_i², an eigenvalue of Q². Thus q_i = 0 or 1. The trace of Q is

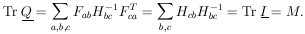
Since the trace of a matrix is invariant under a unitary transformation, the trace always equals the sum of the eigenvalues of the matrix. Therefore M of the eigenvalues of Q are one, and (p - M) are zero. Let U be the unitary matrix which diagonalizes Q (and also (1 - Q)). According to Eq. (35),

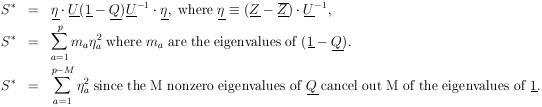
Thus

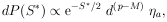
where S* is the square of the radius vector in (p - M)-dimensional space. By definition (see Section 16) this is the ² distribution with (p - M) degrees of freedom.