


AGNs show flux variations over
the entire electromagnetic spectrum. Indeed, variability
was one of the first recognized properties of quasars
51,
82.
Early investigations established that significant
variations ( 0.1 mag)
in the optical brightness of quasars
could occur on time scales as short as days.
0.1 mag)
in the optical brightness of quasars
could occur on time scales as short as days.
Detection of rapid variability in quasars was a remarkable discovery at the time because it implies that the size of the continuum-emitting region must be of order light days (1 lt-day = 2.6 × 1015 cm), based on source coherence arguments: for a source to vary coherently, the entire emitting region must be causally connected, which implies a maximum size for the source based on light-travel time. Suppose, for example, that the brightness of the source doubles in a week; we can immediately conclude that the emitting region must be no larger than one light week in radius on the basis of causality. We might suppose that in fact there are multiple emitting regions varying at random, but the number of such regions must be limited or the stochastic variations would be averaged out. Individually, then, the purported independent regions face a similar size limit from causality, and the conclusion that the emitting regions are very small cannot be avoided. Historically, this is the quasar problem: how can so much energy, the equivalent of as much as trillions of stars, be produced in a region that is about the size of the Solar System?
The detection of quasar variability was a critical part of the argument that AGNs are powered by supermassive black holes. The original arguments for supermassive black holes in AGNs were based on mass constraints from the Eddington limit and size constraints from variability 63. The Eddington limit is the requirement that gravitational forces on an ionized gas exceed outward radiation pressure, which translates to a requirement that
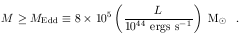
| (1) |
Rapid variations, in some cases on time scales as short as a day, require an emitting region less than a light day in radius, which for a 1044 ergs s-1 AGN corresponds to ~ 104 Rgrav, where Rgrav = GM / c2 is the gravitational radius. Later arguments for supermassive black holes in AGNs focussed on how to power AGNs by gravitational accretion 81. The deep gravitational potential leads to an accretion disk that radiates most strongly across the UV/optical spectrum, and for AGN masses above the Eddington limit, the thermal emission should peak in the near UV. Indeed, then, the broad UV/optical feature known as the "big blue bump" can plausibly be identified with accretion-disk emission. Furthermore, the intense magnetic fields expected in disks could provide a mechanism for jet collimation.