4.3. Discrete Correlation Methods

There are some circumstances under which one might not be able to reasonably interpolate between gaps in data. This can occur (a) when there are a few large gaps in otherwise well-sampled series or (b) when there is reason to believe that the variations might be at least somewhat undersampled. In these cases, interpolation might be highly misleading, and another methodology needs to be employed. The "discrete correlation function" (DCF) ²⁰ method is one where no assumption about light curve behavior needs to be made. The DCF method deals with irregularly sampled data by binning the data in time, as illustrated schematically in Fig. 27. This is an alternative approach to the irregular sampling requirement: instead of requiring that points contributing to CCF() are separated in time by exactly the interval , we time-bin the data by pairing points with time separations in the range ± / 2, where is the width of one time bin. Choice of the binning window is a free parameter, and two examples are shown in Fig. 28.

Figure 27. Part of the light curves from the previous figures, expanded to show DCF bins. The particular example shown is for a time-lag bin width = 4 days and shows the location of the bins, pairing real continuum points with emission-line points within a 4-day window, centered at a shift of 4 days (i.e., emission-line data points shifted by 2-6 days from the continuum points). Note that in this expanded region there are only three emission-line points that fall into the bins; in the range shown here, only two continuum and three emission-line points contribute to the computation of the correlation coefficient.

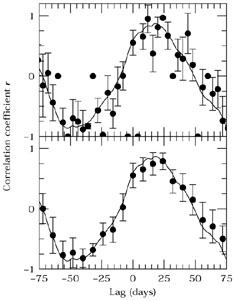
Figure 28. Cross-correlation functions for the Mrk 335 light curve shown in Fig. 23. The DCF values are shown as points with error bars, and the interpolation CCF, as in Fig. 25, is shown as a solid line. The upper panel shows the DCF with a bin width of = 4 days, and the lower panel shows a bin width of = 8 days; with = 4 days, some bins have no data (those with values set to r = -1), but with = 8 days, the DCF is somewhat underresolved.

The principal virtues of the DCF method are (a) that only actual data points are used and (b) that it is possible to assign a statistical uncertainty to the value of the correlation coefficient in each bin. The relative weakness of the DCF is that the data are in some ways underutilized, as is evident in Fig. 27; for a small data set, the DCF method might completely miss a real correlation, although it is less like to find a spurious correlation than is the interpolation method ⁹⁴.

One difficulty of the DCF method is that the number of points per time bin can vary greatly, as can be easily inferred from inspection of Figs. 27 and 28. One solution to this is to vary the width of the time bins to ensure that there are a statistically meaningful number of points in each bin. A method for accomplishing this is the "Z-transformed DCF (ZDCF)" ¹.