

| © CAMBRIDGE UNIVERSITY PRESS 2000 |
22.2. Spherical isotropic models
For systems such as globular clusters it is natural to look for a
description in terms of a distribution function dependent only on the
energy E = v2/2 +
 (r). For these
small stellar systems, it is plausible that they have moved
significantly in the direction of a relaxed quasi-Maxwellian, with a
truncation
radius provided by the tidal environment where the globular cluster moves.
This is the basic physical motivation for solutions of the type
described in the
following section. It should be stressed that the main success of
these truncated models is that they can indeed provide a physically based
description of the global structure of an important class of stellar
systems. For comparison, we will later describe the classical isothermal
sphere
(which has infinite mass) and other tools (models obtained via adiabatic
deformations) that find their best applications to the local
structure of the cores of stellar systems.
(r). For these
small stellar systems, it is plausible that they have moved
significantly in the direction of a relaxed quasi-Maxwellian, with a
truncation
radius provided by the tidal environment where the globular cluster moves.
This is the basic physical motivation for solutions of the type
described in the
following section. It should be stressed that the main success of
these truncated models is that they can indeed provide a physically based
description of the global structure of an important class of stellar
systems. For comparison, we will later describe the classical isothermal
sphere
(which has infinite mass) and other tools (models obtained via adiabatic
deformations) that find their best applications to the local
structure of the cores of stellar systems.
22.2.1. Global truncated (King) models
Consider a spherical distribution of stars f = f
(E) limited to a sphere of
radius rt. The collection of stellar orbits described
by f is thus subject to the condition that f vanishes for
E >
 (rt).
Suppose that the distribution function has the following form
(rt).
Suppose that the distribution function has the following form
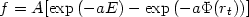 |
(22.5) |
for E <
 (rt)
(and f = 0 otherwise). Here A, a, and
rt
are free constants, defining two scales and one dimensionless
parameter. We may introduce the dimensionless "escape" energy
(rt)
(and f = 0 otherwise). Here A, a, and
rt
are free constants, defining two scales and one dimensionless
parameter. We may introduce the dimensionless "escape" energy
 defined as
defined as
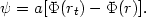 |
(22.6) |
Thus the condition E <
 (rt)
can be written as av2/2 <
(rt)
can be written as av2/2 <
 . The density profile (for
r < rt, i.e.
. The density profile (for
r < rt, i.e.
 > 0) associated with the
distribution function is given by
> 0) associated with the
distribution function is given by
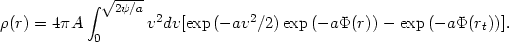 |
(22.7) |
By a simple change of integration variables the density can be written as
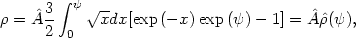 |
(22.8) |
with
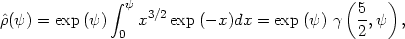 |
(22.9) |
where  is
the incomplete Gamma function
(26). Note that the
density, in this isotropic model, depends on the radial coordinate
only implicitly through the potential
is
the incomplete Gamma function
(26). Note that the
density, in this isotropic model, depends on the radial coordinate
only implicitly through the potential
 (r). For large
values of
(r). For large
values of  we have
we have
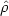 ~
(3
~
(3 1/2/4)
exp(
1/2/4)
exp( ), i.e. it behaves like the
density of non-truncated isothermal models (see following section).
), i.e. it behaves like the
density of non-truncated isothermal models (see following section).
By a suitable rescaling of the radial coordinate
r 
 = r /
= r /
 the self-consistency
relation implied by the Poisson equation can thus be written as
the self-consistency
relation implied by the Poisson equation can thus be written as
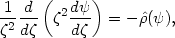 |
(22.10) |
which is to be integrated subject to the boundary conditions
 (0) =
(0) =
 > 0 and
> 0 and
 '(0) = 0. Thus the
scalelength
'(0) = 0. Thus the
scalelength  can be
defined in terms of the central density
can be
defined in terms of the central density
 0
and of the dimensionless depth of the central potential well
0
and of the dimensionless depth of the central potential well
 by means of the relation
by means of the relation
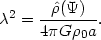 |
(22.11) |
Close to the center the potential well can be approximated by a parabola with
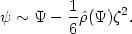 |
(22.12) |
Integrating Eq. (10) out determines
the radius rt as the location where
 vanishes. Thus a one-to-one
correspondence is found between
vanishes. Thus a one-to-one
correspondence is found between
 and
rt /
and
rt /
 . A commonly used
scalelength for this problem is
. A commonly used
scalelength for this problem is
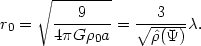 |
(22.13) |
The one-parameter family of
models, usually called King models
(27) (see
Figs. 22.1 - 22.3),
is thus identified either by the value of
 or, more
often, by the value of the concentration index
or, more
often, by the value of the concentration index
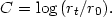 |
(22.14) |
As a model for elliptical galaxies
(28), the required
concentration parameter is in the range
2 < C < 2.35, although the R1/4 profile
is not reproduced in detail. Highly concentrated King models (formally
C 
 ) go in the direction of
the isothermal sphere to be described below. It
should be stressed that, in spite of a being a constant, the velocity
dispersion associated with the distribution function of Eq. (5) is
not a
constant. The velocity dispersion monotonically decreases with radius
and vanishes at the truncation radius (see
Fig. 22.4).
) go in the direction of
the isothermal sphere to be described below. It
should be stressed that, in spite of a being a constant, the velocity
dispersion associated with the distribution function of Eq. (5) is
not a
constant. The velocity dispersion monotonically decreases with radius
and vanishes at the truncation radius (see
Fig. 22.4).
The radius r0 is sometimes confused with the "core
radius" rc of the
projected density distribution, usually defined as the location where the
projected density has dropped to one half of its central value. With the
definition of Eq. (13) the identification is correct for the
isothermal sphere (see below), and it is reasonable for concentrated King
models (29),
while at lower values of
 the ratio
r0/rc changes
significantly with
the ratio
r0/rc changes
significantly with  .
.
Applications of these models to globular clusters have been very successful.
The globular clusters of our Galaxy
(30) are generally
well fitted by King models with concentration parameter in the range
0.5 < C < 2 (see Fig. 22.5);
some are even more concentrated, but they are generally considered to be in
a "post-core-collapse" phase, since the onset of the gravitational
catastrophe (31)
is known to take place at

 7.4.
One can take full advantage of the equilibrium sequence by arguing
that the identifying parameters (total mass, central velocity
dispersion, and
concentration) can change as a result of evolutionary processes (such as
evaporation and disk-shocking), while the underlying model retains its King
appearance (32). By this
representation it is possible to follow the evolution of a whole
population of globular clusters in
a galaxy with a rather handy algorithm
(33), thus clarifying many
of the interesting correlations in the relevant parameter space observed
for the clusters of our Galaxy.
7.4.
One can take full advantage of the equilibrium sequence by arguing
that the identifying parameters (total mass, central velocity
dispersion, and
concentration) can change as a result of evolutionary processes (such as
evaporation and disk-shocking), while the underlying model retains its King
appearance (32). By this
representation it is possible to follow the evolution of a whole
population of globular clusters in
a galaxy with a rather handy algorithm
(33), thus clarifying many
of the interesting correlations in the relevant parameter space observed
for the clusters of our Galaxy.
We now consider the spherical analogue of the isothermal slab solution described in section 14.1 (in the context of the vertical equilibrium of a disk). That calculation was especially instructive, as a very simple case of a stellar dynamical study with distribution function priority. We may recall that the isothermal slab implied a constant gravity field at large distances from the plane [see Eq. (14.9)], so that, as a model of a galaxy disk, its interest was mostly for a self-consistent description of the vicinity of the equatorial plane.
Similarly, besides its general interest as indicative of the divergences intrinsic to the hypothesis of a fully relaxed stellar system, the spherical solution to be described below provides a useful representation of the local behavior of many stellar systems in their central regions. It can clarify some of the properties of the more physical King models (which have been successfully applied to the interpretation of the global luminosity profiles of globular clusters). In addition, it also turns out to describe much of the structure inside the half mass radius of the partially relaxed, finite mass models that will be found to incorporate the R1/4 profile (to be described in section 22.3).
If we take the distribution function
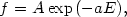 |
(22.15) |
with no restrictions on the star velocities, we get an isothermal equation of state given by
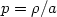 |
(22.16) |
with
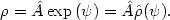 |
(22.17) |
Here we have introduced the dimensionless potential
 = -a
= -a
 (r). Note that
the two constants A and a are
dimensional parameters that may be used in order to match some physical
scales of the system under investigation (e.g., the radius and the central
velocity dispersion in the core of a galaxy). In contrast with the King
models, there are no free dimensionless parameters available here. These
relations are in analogy to those of section 14.1.1 and should be
compared with
the corresponding equations of the previous section. The fully
self-consistent problem requires the solution of the Poisson equation
(r). Note that
the two constants A and a are
dimensional parameters that may be used in order to match some physical
scales of the system under investigation (e.g., the radius and the central
velocity dispersion in the core of a galaxy). In contrast with the King
models, there are no free dimensionless parameters available here. These
relations are in analogy to those of section 14.1.1 and should be
compared with
the corresponding equations of the previous section. The fully
self-consistent problem requires the solution of the Poisson equation
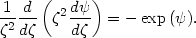 |
(22.18) |
The scalelength  is
defined via the relation [see Eq. (11)]
is
defined via the relation [see Eq. (11)]
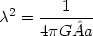 |
(22.19) |
If we look for a solution with finite central density the natural
boundary conditions are  (0) =
(0) =
 and
and
 '(0) = 0. Since
no free dimensionless parameters are available, here we can choose the value
of
'(0) = 0. Since
no free dimensionless parameters are available, here we can choose the value
of  in such a way that
in such a way that
 =
r0 (see Eq. (13). As is well
known in studies of polytropic stars, the isothermal solution beyond the
scale r0 becomes asymptotically close to
=
r0 (see Eq. (13). As is well
known in studies of polytropic stars, the isothermal solution beyond the
scale r0 becomes asymptotically close to
 ~
r-2, thus leading to
an integrated mass increasing linearly with radius and making it
inapplicable to describe the global profiles of stellar systems.
~
r-2, thus leading to
an integrated mass increasing linearly with radius and making it
inapplicable to describe the global profiles of stellar systems.
In the central regions [basically at radii r = O(r0)], the density profile that is obtained numerically, when projected along the line-of-sight is found to match the general behavior of galaxy cores. The projected density (here R denotes the projected radius) is very close to the so-called modified Hubble profile
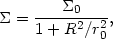 |
(22.20) |
which can be traced to a volume density profile (34) of the form
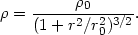 |
(22.21) |
Obviously, the latter expressions find frequent applications because of their analytical simplicity.
One special solution with a singularity at the center is obtained when the
condition of finite central density is dropped. This singular
isothermal sphere corresponds to
 = -2
ln(
= -2
ln( /
21/2), which
solves Eq. (18) exactly. Here the model loses the chacterization in
terms of the central density and becomes "self-similar". The
constants A and a are related to the constants b
and V0 of the
logarithmic spherical mass model of section 21.1.3 via the relations
a = 2/V02 and b = 21/2
/
21/2), which
solves Eq. (18) exactly. Here the model loses the chacterization in
terms of the central density and becomes "self-similar". The
constants A and a are related to the constants b
and V0 of the
logarithmic spherical mass model of section 21.1.3 via the relations
a = 2/V02 and b = 21/2
 , with
, with
 given by
Eq. (19).
The singular isothermal sphere presents close analogies with the isothermal
self-similar disk described in section 14.3.2, in relation to the
logarithmic
potential that is found and to the type of divergences occurring at
small and large radii. For the associated orbit structure we may thus
refer to section 21.1.3.
given by
Eq. (19).
The singular isothermal sphere presents close analogies with the isothermal
self-similar disk described in section 14.3.2, in relation to the
logarithmic
potential that is found and to the type of divergences occurring at
small and large radii. For the associated orbit structure we may thus
refer to section 21.1.3.
Historically, the study of the isothermal sphere finds its roots in the
theory of stellar structure, in relation to the Lane-Emden equation for
polytropic star models
(35). We recall that the
isotropic distribution function
f = A(- E)s for E < 0 (and
f = 0 otherwise), with
 = 0 defining the
surface of the associated stellar system, generates a density distribution
= 0 defining the
surface of the associated stellar system, generates a density distribution
 (r) =
B[-
(r) =
B[-  (r)]s+3/2. Here A, B are
constants. The Poisson equation thus becomes the same as the equation for a
polytropic sphere
(36) with index
n = s + 3/2. For the latter equation analytical
solutions are known for
n = 0, 1, 5. The case with n = 5 (with infinite radius)
is often considered for its simple analytical structure
(37). In particular the
associated Plummer density-potential pair is given by
(r)]s+3/2. Here A, B are
constants. The Poisson equation thus becomes the same as the equation for a
polytropic sphere
(36) with index
n = s + 3/2. For the latter equation analytical
solutions are known for
n = 0, 1, 5. The case with n = 5 (with infinite radius)
is often considered for its simple analytical structure
(37). In particular the
associated Plummer density-potential pair is given by
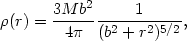 |
(22.22) |
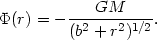 |
(22.23) |
The integrated mass is given by
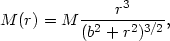 |
(22.24) |
so that the half-mass radius occurs at
rM  1.3b. The mean-square velocity is exactly
<v2> =
-
1.3b. The mean-square velocity is exactly
<v2> =
- (r) / 2 and the
projected density is given by
(r) / 2 and the
projected density is given by
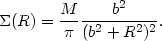 |
(22.25) |
22.2.3. Galaxy cores and anisotropic models obtained via adiabatic growth
We have noted at the beginning of the previous subsection that different
emphasis can be given to the global or to a local
application of stellar dynamical models. On the small scale (r
<< rM) many models, such as King
models or the ones that will be introduced in
section 22.3, are characterized by a
quasi-isothermal core, in the sense that they behave approximately as the
(regular) isothermal sphere of
section 22.2.2. On the other hand nuclei of
galaxies have long been suspected to host massive point-like density
concentrations (possibly black holes). It is thus of great interest to
see whether
adequate self-consistent models can be constructed where the field is
due to the
sum of the contributions of the stellar system and of a central point-mass.
Clearly a comparison of the properties of these models with high resolution
photometric and spectroscopic observations should eventually tell which
galaxies host a central massive "black hole" and which do not. Major
projects have
been undertaken in the last few years focusing on these
issues (38).
Either by means of stellar dynamical studies alone (in particular, for disk
galaxies, such as M 31, NGC 3115, NGC 4594, our Galaxy, and for
ellipticals (39), such
as M 32 and
NGC 3377) or with the help of kinematical data from
gas orbiting close to the
central nucleus (see the spectacular cases of the giant elliptical
M 87
and of the spiral galaxy NGC 4258 = M 106; see
Fig. 22.6) convincing evidence has been
accumulating for central black holes with masses in the range
2 × 106 - 3 × 109
M .
.
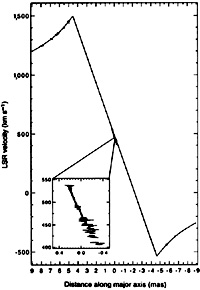 |
Figure 22.6. A radio observation suggesting the presence of a massive black hole at the center of the galaxy M 106 (Fig. 3 from Miyoshi, M., Moran, J., Herrnstein, J., Greenhill, L., et al. 1995, Nature (London), 373, 127). The plot gives the line-of-sight velocity as a function of radial distance (in milliarcseconds) from the center, along the major axis of the observed molecular disk, with data superimposed on a model curve described in the cited paper. At the distance of the object (estimated to be 6.4 Mpc), 8 mas define a length of 0.25 pc. |
Kinematical data are probably crucial to decide whether a central point-mass exists. Still it has been noted that, in the innermost regions (where the R1/4-like profile is usually smeared out by seeing from the ground (40)), in some cases the luminosity profile, when studied at sufficiently high spatial resolution, does flatten out into a core structure, while in others the profile increases basically as a power-law (41), as far in as it is possible to observe. With the aid of the Hubble Space Telescope, for a sample of dozens of ellipticals (and bulges) this behavior has been traced down to a scale of 1pc from the center. Curiously, some of the parameters that characterize the galactic nuclear regions are found to correlate strongly with more global parameters.
In this short subsection we will not go further into this fascinating
subject, but we will restrict our attention to some modeling issues that are
found to be interesting because of their simple physical motivation. In
contrast to the case without a central point mass, for which a core
structure is naturally
expected, in the presence of a 1/r singularity in the potential the
stellar system should display a central cusp in its density
distribution. In a study of this type, one important parameter is
clearly the ratio
M /
Mc of
the mass of the "black hole" to the mass of the core of the large-scale
stellar density distribution.
/
Mc of
the mass of the "black hole" to the mass of the core of the large-scale
stellar density distribution.
Originally, much of the attention was drawn to the case of
a black hole inside a collisional environment, such as that at the
center of a
globular cluster. Steady-state solutions of the Fokker-Planck equation were
sought and constructed, thus applicable to timescales longer than the
relevant two-body relaxation time
(42).
In the regime of small masses of the central black hole, under the
assumption that binary stars are unimportant, the cusp that is found is
approximately given by
 ~
r-7/4. In the following years, motivated by some of
the observational
studies mentioned above, the attention changed to the case of the more
collisionless galaxy cores. A recent revival of interest in collisional
steady-state solutions
(43) is
motivated by the fact that one may imagine even the center of a galaxy
to produce a collisional cusp via merging of small star clumps.
~
r-7/4. In the following years, motivated by some of
the observational
studies mentioned above, the attention changed to the case of the more
collisionless galaxy cores. A recent revival of interest in collisional
steady-state solutions
(43) is
motivated by the fact that one may imagine even the center of a galaxy
to produce a collisional cusp via merging of small star clumps.
The collisionless case suggests the likely presence of significant anisotropies very close to the central point mass. There radial orbits would feel selectively the influence of the central singularity. A first simple study can be performed by focusing on the region outside such a black hole dominated environment and can be obtained in terms of the so-called "loaded polytropes" (44). The basic idea is to see in such an outer region how the Lane-Emden equation is modified, thus reducing the discussion to that of a modified (isotropic) hydrostatic equilibrium with an assumed equation of state. One interesting finding of this much simplified description has been to show that a cusp structure forms, with properties that depend little on the polytropic index.
A more elegant construction of self-consistent stellar dynamical models can be made under the assumption that the central black hole grows slowly (on a time much longer than the relevant dynamical timescale) inside a pre-existing collisionless stellar system (thus on a time shorter than the relaxation time). In a spherical adiabatic growth (45) the orbits associated with the distribution function are modified but conserve their angular momentum and their radial action. The process thus shows in a very intuitive way how anisotropy can be generated out of an initially isotropic system by the growth of the central mass.
Without entering in all the details, we would like to record here the structure of the equations that describe spherical adiabatic evolution. Suppose we separate the potential in two parts, so that the energy integral is given by
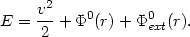 |
(22.26) |
Here
 ext0
is an external potential, while
ext0
is an external potential, while
 0 is the
self-consistent potential generated by the density associated with the
distribution function f0(E, J)
describing the stellar system. We
recall that the radial action Jr is defined as
0 is the
self-consistent potential generated by the density associated with the
distribution function f0(E, J)
describing the stellar system. We
recall that the radial action Jr is defined as
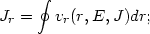 |
(22.27) |
the function vr and the integral between the two turning points depend on the sum of the external and of the self-consistent potentials.
Now we can imagine that the external potential
be varied slowly, by changing one parameter
 from its initial value
from its initial value
 0, so that
it becomes
0, so that
it becomes
 ext(r).
This change will induce a change in the self-consistent potential from
ext(r).
This change will induce a change in the self-consistent potential from
 0(r)
to
0(r)
to  (r). In this
slow
process the radial action and the angular momentum are conserved, while the
energy is not. So we may imagine to start from an orbit characterized by
(E(0), J) in the potential
(r). In this
slow
process the radial action and the angular momentum are conserved, while the
energy is not. So we may imagine to start from an orbit characterized by
(E(0), J) in the potential
 0(r) +
0(r) +
 ext0(r) and arrive at an
orbit characterized by (E, J) in the potential
ext0(r) and arrive at an
orbit characterized by (E, J) in the potential
 (r) +
(r) +
 ext(r)
with the condition:
ext(r)
with the condition:
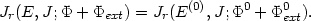 |
(22.28) |
This relation should be interpreted as a mapping between the "initial" value of the energy E(0) and the "final" value of the energy E required for the radial action to remain constant. In other words this gives implicitly a relation E(0) = E(0)(E, J). If we start from a distribution of stellar orbits f0, the final distribution function will thus be given by
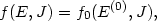 |
(22.29) |
with E(0) determined from Eq. (28). Self-consistency requires
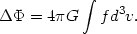 |
(22.30) |
These non-linear equations can be solved numerically (e.g., by iteration
procedures) to derive the effects of adiabatic evolution. In particular
one may consider the situation where
 ext0
= 0 and f0 = f0(E) describes a
non-singular isothermal sphere [see Eq. (15)], and ask what will
be the final distribution function f (E, J) for
ext0
= 0 and f0 = f0(E) describes a
non-singular isothermal sphere [see Eq. (15)], and ask what will
be the final distribution function f (E, J) for
 ext = - G
M
ext = - G
M /
r. The influence radius of the black hole is thus given by
r
/
r. The influence radius of the black hole is thus given by
r =
aG
M
=
aG
M ,
while the mass of the core can be defined from
r0 = aGMc. The density cusp is found
to be characterized by
,
while the mass of the core can be defined from
r0 = aGMc. The density cusp is found
to be characterized by
 ~
r-3/2 and associated with a kinematical cusp
<v2> ~ G
M
~
r-3/2 and associated with a kinematical cusp
<v2> ~ G
M /
r. For a small black hole the density cusp emerges
from the core
region, while for large black holes the transition to the outer
~ r-2 isothermal behavior occurs via an intermediate
~ r-5/2 profile, with
no distinct core left (see Fig. 22.7). The
cusp is quasi-isotropic, with a small tangential bias at intermediate
radii. These conclusions are changed if one starts
from initial functions significantly different from that of the non-singular
isothermal sphere. The extension to the case where some rotation and
flattening are present is not trivial.
/
r. For a small black hole the density cusp emerges
from the core
region, while for large black holes the transition to the outer
~ r-2 isothermal behavior occurs via an intermediate
~ r-5/2 profile, with
no distinct core left (see Fig. 22.7). The
cusp is quasi-isotropic, with a small tangential bias at intermediate
radii. These conclusions are changed if one starts
from initial functions significantly different from that of the non-singular
isothermal sphere. The extension to the case where some rotation and
flattening are present is not trivial.
Part of the structure of the solutions obtained by adiabatic growth can be
clarified analytically. For this purpose one may refer to regions of phase
space where the actions in the key mapping relation (28) can be
approximated analytically (see Chapter 21 for the Keplerian, the
logarithmic, and
the harmonic potentials). Another limit where one can proceed
semi-analytically is the linear regime, where the departures
f1 = f - f0 and
 1 =
1 =
 -
-
 0 from the
initial configuration are small because
the change in the external potential
0 from the
initial configuration are small because
the change in the external potential

 ext is small. The
linearized equations for adiabatic changes are
(46)
ext is small. The
linearized equations for adiabatic changes are
(46)
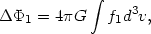 |
(22.31) |
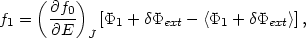 |
(22.32) |
where E is given by Eq. (26) and the angle brackets denote a bounce orbit average over the unperturbed orbits
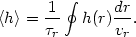 |
(22.33) |
Here  r is the
bounce time between the radial turning points
[see Eq. (13.15)]. These equations are a somewhat subtle zero-frequency
limit of the linear stability equations (see Chapter 23); they are also
well known within the plasma community
(47).
r is the
bounce time between the radial turning points
[see Eq. (13.15)]. These equations are a somewhat subtle zero-frequency
limit of the linear stability equations (see Chapter 23); they are also
well known within the plasma community
(47).
It is not clear how these tools can give a realistic representation of galactic nuclei (see also section 25.1.3 in Part five). They have been shown here mostly because they define an interesting and physically guided device to construct self-consistent equilibrium distribution functions with a central point mass and because they represent an instructive case. A scenario of this type and similar techniques may turn out to be useful to describe other situations of interest in stellar dynamics.
26 See Abramowitz, M., Stegun, I.A. (1970), op.cit., definition 6.5.2 Back.
27 King, I. R.
(1965), Astron. J., 70, 376;
(1966), Astron. J., 71, 64;
Michie, R.W.
(1963), Mon. Not. Roy. Astron. Soc., 125, 127
and Michie, R.W., Bodenheimer, P.H.
(1963), Mon. Not. Roy. Astron. Soc., 126, 269
considered the more general anisotropic distribution function, where
E  E + cJ2
Back.
E + cJ2
Back.
28 Kormendy, J. (1978), Astrophys. J., 218, 333; King, I.R. (1978), Astrophys. J., 222, 1 Back.
29 Peterson, C.J., King, I.R. (1975), Astron. J., 80, 427 Back.
30 Djorgovski, S.G., Meylan, G. (1994), Astron. J., 108, 1292 Back.
31 Antonov, V.A. (1962), Vest. Lenigrad Univ., 7, 135, translated in Proceedings IAU Symp. 113, ed. J. Goodman, P. Hut, Reidel, Dordrecht, p. 525; Lynden-Bell, D., Wood, R. (1968), Mon. Not. Roy. Astron. Soc., 138, 495 Back.
32 King, I.R. (1966), Astron. J., 71, 64; Prata, S.W. (1971), Astron. J., 76, 1017 and 1029; Chernoff, D.F., Kochanek, C.S., Shapiro, S.L. (1986), Astrophys. J., 309, 183; Chernoff, D.F., Shapiro, S.L. (1987), Astrophys. J., 322, 113 Back.
33 Vesperini, E. (1997), Mon. Not. Roy. Astron. Soc., 287, 915 Back.
34 See Rood, H.J., Page, T.L., Kintner, E.C., King, I.R. (1972), Astrophys. J., 175, 627 Back.
35 Eddington, A.S. (1926), Internal constitution of stars, Cambridge University Press, Cambridge; Chandrasekhar, S. (1939), An introduction to the theory of stellar structure, University of Chicago, Chicago (reprinted by Dover, New York); Saslaw, W.C. (1985), Gravitational physics of stellar and galactic systems, Cambridge University Press, Cambridge; see also Betti, E. (1880), Nuovo Cimento, 7, 26 Back.
36 see also Vandervoort, P.O. (1980), Astrophys. J., 240, 478 Back.
37 Plummer, H.C. (1915), Mon. Not. Roy. Astron. Soc., 76, 107 Back.
38 See, for example, Kormendy, J., Richstone, D. (1995), Ann. Rev. Astron. Astrophys., 33, 581; Crane, P., Stiavelli, M., King, I.R., Deharveng, J.M., et al. (1993), Astron. J., 106, 1371; Faber, S.M., Tremaine, S., Ajhar, E.A., Byun, Y-I. et al., (1997), Astron. J., 114, 1771, and the many papers cited therein. In particular, for M 32 see van der Marel, R.P., de Zeeuw, P.T., Rix, H-W., Quinlan, G.D. (1997), Nature, 385, 610; for M87 see Harms, R.J., Ford, H.C., Tsvetanov, Z.I., Hartig, G.F. et al. (1994), Astrophys. J. Letters, 435, L35; for M 106 see Miyoshi, M., Moran, J., Herrnstein, J., Greenhill, L., et al. (1995), Nature, 373, 127 Back.
39 Other objects not mentioned here are also likely to possess a massive central black hole; e.g., for NGC 1399 see Stiavelli, M., Møller, P., Zeilinger, W.W., (1993), Astron. Astrophys., 277, 421 Back.
40 The failure of the R1/4 profile in the innermost regions was already noted by Lauer, T. (1985), Astrophys. J., 292, 104 and by others Back.
41 The classical case is that of M 87; see Young, P.J., Westphal, J.A., Kristian, J., Wilson, C.P., Landauer, F.P. (1978), Astrophys. J., 221, 721 Back.
42 Peebles, P.J.E. (1972), Astrophys. J., 178, 371; Bahcall, J.N., Wolf, R.A. (1976), Astrophys. J., 209, 214 Back.
43 Evans, N.W., Collett, J.L.
(1997), Astrophys. J. Letters, 480, L103
show that a steady-state cusp with
 ~
r-4/3 is a
self-consistent solution of the collisional Boltzmann equation
Back.
~
r-4/3 is a
self-consistent solution of the collisional Boltzmann equation
Back.
44 Huntley, J.M., Saslaw, W.C. (1975), Astrophys. J., 199, 328 Back.
45 Peebles, P.J.E. (1972), Gen. Rel. Grav., 3, 63; Young, P.H. (1980), Astrophys. J., 242, 1232; Goodman, J., Binney, J.J. (1984), Mon. Not. Roy. Astron. Soc., 207, 511; Lee, M.H., Goodman, J. (1989), Astrophys. J., 343, 594; Cipollina, M., Bertin, G. (1994), Astron. Astrophys., 288, 43; Quinlan, G.D., Hernquist, L., Sigurdsson, S. (1995), Astrophys. J., 440, 554. The effects of a slowly growing (and also of a fast growing) black hole inside an initially triaxial model have been studied recently using N-body simulations by Merritt, D., Quinlan, G.D. (1998), Astrophys. J., 498, 625 Back.
46 Cipollina, M. (1992), Tesi di laurea, Pisa University; Cipollina, M., Bertin, G. (1994), Astron. Astrophys., 288, 43 Back.
47 See Antonsen, T.M., Lee, Y.C. (1982), Phys. Fluids, 25, 132 Back.