2.1.2. The Direct Method

Direct abundance measurements can be made when one is able to measure the faint emission lines which are important diagnostics of electron temperature, T_e. The abundance of any ion relative to H⁺ derived from the ratio of the intensity of a transition to the intensity of H is given by

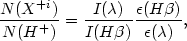(2.1)

where () represents the volume emission coefficient for a given emission line . For collisionally-excited lines in the low-density limit, the analysis in section 5.9 of Osterbrock (1989) applies.

When T_e has been measured, the volume emission coefficient for a collisionally-excited line is given by

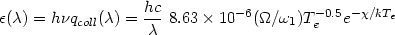(2.2)

where is the collision strength for the transition observed, ₁ is the statistical weight of the lower level, and is the excitation energy of the upper level. contains the physics in the calculation; it represents the electron-ion collision cross-section averaged over a Maxwellian distribution of electron velocities relative to the target ion at the relevant temperature. Thus has a mild temperature dependence, which can introduce a trend in abundance ratios if not accounted for.

Note on collision strengths: the vast majority of these values are computed, not experimental. This does not mean that they have zero uncertainty! A recent example is given by the case of [S III] (Tayal & Gupta 1999). This new 27-state R-matrix calculation resulted in changes of approximately 30% in the collision strengths for optical and IR forbidden transitions from earlier calculations. This shows that even for commonly-observed ions the atomic data is still in a state of flux. Observers should take into account the probable uncertainty in atomic data when estimating errors in abundances.

Another thing to account for is the fact that ionized nebulae are not strictly isothermal. Because [O III] is usually the most efficient coolant, the thermal balance at any point in an H II region depends on the local abundance of O⁺², as well as the local radiation field. The ion-weighted electron temperature for a given ion can vary with respect to T(O III) in a predictable way (Garnett 1992), depending largely on the metallicity. Figure 2 shows a plot of measured electron temperatures for [O III], [S III], [O II], and [N II] compared with the relationships derived from model photoionized nebulae (solid lines). The measured temperatures show correlations which agree quite well with the model relations, although there is quite a bit of scatter in the [O II] temperatures, and there may be a slight offset between T[S III] and the predicted relation, which may be real or an observational artifact. These results indicate that the photoionization models provide a reliable predictor of the thermal properties of H II regions.

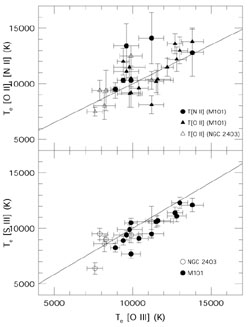Figure 2. Comparison of electron temperatures derived from [O III], [O II], [N II], and [S III] measurements for H II regions in NGC 2403 and M101. The straight lines show the correlations predicted by photoionization models (Garnett 1992).

For recombination lines, the emission coefficient is given by

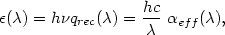(2.3)

where _eff() is the "effective" recombination coefficient for the recombination line . _eff incorporates the physics, including the cross-section for electron-ion recombination and the probability that a given recombination will produce the given emission line. values for H vary as roughly T_e^-1; individual lines have mildly different T dependences, but recombination line ratios are only weakly dependent on T, and quite insensitive to n_e for densities less than 10⁶ cm^-3.

Most astronomers are familiar with the bright H I Balmer and He I recombination lines in the optical spectrum of ionized nebulae. Heavier elements also emit a recombination spectrum, and O I, O II, C II, N I, N II and other permitted lines have been observed in PNs and the Orion Nebula. In principle, such recombination lines could yield more accurate abundances than the forbidden lines, because their emissivities all have roughly the same T dependence. In practice, the recombination lines scale roughly with element abundance, so even for O and C the RLs are typically fainter than 1% of H, making them too faint to observe routinely in extragalactic H II regions. It is observed that recombination lines in some PNs give much higher abundances than the corresponding forbidden lines from the same ions (Liu et al. 1995, 2000; Garnett & Dinerstein 2001, 2002), and there is currently a raging debate over whether the recombination lines or the the forbidden lines provide more reliable abundances.

Measurements of infrared collisionally-excited fine-structure lines are gaining ground with the launch of the ISO spacecraft, and with the upcoming SIRTF, SOFIA, and FIRST missions. Recognizing that 5-10 eV for UV forbidden lines, 2-3 eV for optical forbidden lines, and < 0.2 eV for IR fine structure lines with > 7µm, we see that the exponential term in Equation 2.2 goes to nearly unity, and the IR lines have a weak temperature dependence. Thus it should be possible to determine accurate abundances free of concerns over temperature fluctuations. One caveat is that the very important [O III] and [N III] fine-structure lines are sensitive to density, suffering from collisional de-excitation at n_e 1000 cm^-3, so density fluctuations could introduce large uncertainties. Fine structure lines from Ne, S, and Ar in the 7-20µm range, however, are not so sensitive to density.

For extragalactic H II regions, the main limitations on IR observations so far have been small telescopes, high background, and short spacecraft lifetimes. Nevertheless, ISO is providing some information on H II regions in the Galaxy and other Local Group galaxies (and luminous starbursts), and the future missions promise even better data.