2.1.3. "Empirical" (Strong-Line) Calibrations

In many cases T_e can not be measured, either because the nebula is too faint or it is so cool that the temeprature-sensitive diagnostic lines (for example [O III] 4363) are too weak. Thus, there is interest in having an abundance indicator that uses the strong forbidden lines.

Pagel et al. (1979) identified the line intensity ratio

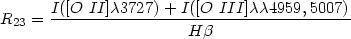(2.4)

as an indicator of O/H in H II regions. They noted, based on a sample of extragalactic H II regions, that the measured T_e, O/H, and R₂₃ were all correlated. This works because of the relationship between O/H and nebular cooling: the cooling in the ionized gas is dominated by emission in IR fine-structure lines (primarily the [O III] 52µm and 88µm lines), so as O/H increases, the nebula becomes cooler. In response, the optical forbidden lines, especially the [O III] lines, become weaker as O/H increases (excitation goes down as T decreases).

The R₂₃ vs. O/H relation is fairly well calibrated empirically (based on abundances using the direct method) for log O/H between -3.5 and -4.0 (Edmunds & Pagel 1984). For higher O/H, the strong-line method breaks down because few measurements of T_e exist; only two measurements have been made for H II regions with roughly solar O/H (Kinkel & Rosa 1994; Castellanos et al. 2001). In this regime, the relation has been calibrated using photoionization models (which I'll discuss later) that may have systematic errors. One other complication is that for log O/H < -3.8, the relation between R₂₃ and O/H reverses, such that R₂₃ decreases with decreasing abundance. The relation thus becomes double-valued, and at the turn-around region the uncertainties in O/H are much larger. This occurs because at very low metallicities the IR fine-structure lines no longer dominate the cooling because there are too few heavy elements. As a result the forbidden lines more directly reflect the abundances in the gas.

This double-valued nature of R₂₃ has led some to seek other strong-line diagnostics. The ratio [O III]/[N II] (Alloin et al. 1979; Edmunds & Pagel 1984) has been promoted to break the degeneracy in R₂₃. This ratio does appear to vary monotonically with O/H, although the observational scatter generally is larger than for R₂₃. More recently, the emission line ratio

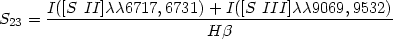(2.5)

has been calibrated as an indicator of O/H by Díaz & Pérez-Montero (2000). S₂₃ has the advantage of varying monotically over the range -4.3 < log O/H < -3.7 in which R₂₃ becomes ambiguous. S₂₃ does become double-valued for O/H > -3.4. Where this relation breaks down is uncertain at present because there are too few measurements. In addition, the ratio [N II]6583 / H has been promoted as another possible measure of O/H (van Zee et al. 1998; Denicoló, Terlevich & Terlevich 2002). [N II] / H varies monotonically with O/H over the entire range over which it is calibrated, but the scatter is quite large, especially at low values of O/H in dwarf irregular galaxies. Note that S₂₃ and [N II] / H are employed here as measures of the oxygen abundance, not sulfur or nitrogen and are calibrated by direct measurements of O/H. Thus, non-solar abundance ratios are not a concern.

At the same time, there are several limitations.

1. None of these strong-line diagnostics is well calibrated for log O/H > -3.5. At higher metallicities, the calibration is largely derived from photoionization models.
2. The accuracy of each of these calibrations is quite limited. For R₂₃ the usual quoted uncertainty is ±0.2 dex, which is roughly the scatter; in the turnaround region, the uncertainty is significantly larger. The accuracy of S₂₃ is probably about the same; although there are few data points to pin down the scatter at the present time. The scatter in [N II] / H is significantly larger, about ±0.3 dex; most of this scatter is real, not observational.
3. The strong-line abundance relations are subject to systematic errors, because the forbidden-line strengths depend on the stellar effective temperature and ionization parameter as well as abundances. If a galaxy has a low star formation rate and only low-luminosity H II regions with cooler O stars, the empirical calibration could give a systematically different O/H than a galaxy with many of the most massive O stars and luminous giant H II regions.