2.5. Vacuum energy in cosmology

So what does this have to do with cosmology? The interesting fact about vacuum energy is that it results in accelerated expansion of the universe. From Eq. (13), we can write the acceleration 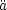in terms of the equation of state p = w of the matter in the universe,

(49)

For ordinary matter such as pressureless dust w = 0 or radiation w = 1/3, we see that the gravitational attraction of all the stuff in the universe makes the expansion slow down with time, < 0. But we have seen that a cosmological constant has the odd property of negative pressure, w = - 1, so that a universe dominated by vacuum energy actually expands faster and faster with time, > 0. It is easy to see that accelerating expansion helps with the age problem: for a standard matter-dominated universe, a larger Hubble constant means a younger universe, t₀ H₀^-1. But if the expansion of the universe is accelerating, this means that H grows with time. For a given age t₀, acceleration means that the Hubble constant we measure will be larger in an accelerating cosmology than in a decelerating one, so we can have our cake and eat it too: an old universe and a high Hubble constant! This also resolves the old dispute between the observers and the theorists. Astronomers measuring the density of the universe use local dynamical measurements such as the orbital velocities of galaxies in a cluster. These measurements are insensitive to a cosmological constant and only measure the matter density _M of the universe. However, geometrical tests like the cosmic microwave background which we will discuss in the Sec. 3 are sensitive to the total energy density _M + . If we take the observational value for the matter density _M = 0.2 - 0.3 and make up the difference with a cosmological constant, = 0.7 - 0.8, we arrive at an age for the universe in excess of 13 Gyr, perfectly consistent with the globular cluster data.

In the 1980s and 1990s, there were some researchers making the argument based on the age problem alone that we needed a cosmological constant [6]. But the case was hardly compelling, given that the CMB results indicating a flat universe had not yet been measured, and a low-density universe presented a simpler alternative, based on a cosmology containing matter alone. However, there was another observation that pointed clearly toward the need for : Type Ia supernovae (SNIa) measurements. A detailed discussion of these measurements is beyond the scope of these lectures, but the principle is simple: SNeIa represent a standard candle, i.e. objects whose intrinsic brightness we know, based on observations of nearby supernovae. They are also extremely bright, so they can be observed at cosmological distances. Two collaborations, the Supernova Cosmology Project [7] and the High-z Supernova Search [8] obtained samples of supernovae at redshifts around z = 0.5. This is far enough out that it is possible to measure deviations from the linear Hubble law v = H₀d due to the time-evolution of the Hubble parameter: the groups were able to measure the acceleration or deceleration of the universe directly. If the universe is decelerating, objects at a given redshift will be closer to us, and therefore brighter than we would expect based on a linear Hubble law. Conversely, if the expansion is accelerating, objects at a given redshift will be further away, and therefore dimmer. The result from both groups was that the supernovae were consistently dimmer than expected. Fig. 2 shows the data from the Supernova Cosmology Project [9], who quoted a best fit of _M 0.3, 0.7, just what was needed to reconcile the dynamical mass measurements with a flat universe!

Figure 2. Data from the Supernova Cosmology project [9]. Dimmer objects are higher vertically on the plot. The horizontal axis is redshift. The curves represent different choices of M and . A cosmology with M = 1 and = 0 is ruled out to 99% confidence, while a universe with M = 0.3 and = 0.7 is a good fit to the data.

So we have arrived at a very curious picture indeed of the universe: matter, including both baryons and the mysterious dark matter (which I will not discuss in any detail in these lectures) makes up only about 30% of the energy density in the universe. The remaining 70% is made of of something that looks very much like Einstein's "greatest blunder", a cosmological constant. This dark energy can possibly be identified with the vacuum energy predicted by quantum field theory, except that the energy density is 120 orders of magnitude smaller than one would expect from a naive analysis. Few, if any, satisfying explanations have been proposed to resolve this discrepancy. For example, some authors have proposed arguments based on the Anthropic Principle [10] to explain the low value of , but this explanation is controversial to say the least. There is a large body of literature devoted to the idea that the dark energy is something other than the quantum zero-point energy we have considered here, the most popular of which are self-tuning scalar field models dubbed quintessence [11]. A review can be found in Ref. [12]. However, it is safe to say that the dark energy that dominates the universe is currently unexplained, but it is of tremendous interest from the standpoint of fundamental theory. This will form the main theme of these lectures: cosmology provides us a way to study a question of central importance for particle theory, namely the nature of the vacuum in quantum field theory. This is something that cannot be studied in particle accelerators, so in this sense cosmology provides a unique window on particle physics. We will see later, with the introduction of the idea of inflation, that vacuum energy is important not only in the universe today. It had an important influence on the very early universe as well, providing an explanation for the origin of the primordial density fluctuations that later collapsed to form all structure in the universe. This provides us with yet another way to study the "physics of nothing", arguably one of the most important questions in fundamental theory today.