3.3. Fractal scaling

The number of neighbors - on average - a galaxy has within a sphere of radius r is just the integral

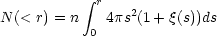(4)

When this function follows a power-law N( < r) r^D₂, the exponent is the correlation dimension, and the point pattern is said to verify fractal scaling. There is no doubt that up to a given scale the galaxy distribution fits rather well the fractal picture. However, some controversy regarding the extent of the fractal regime has motivated an interesting debate [26, 27, 28, 7]. Nevertheless, the new data is showing overwhelming evidence that the correlation dimension is a scale dependent quantity. Different authors [29, 30, 31, 32, 33, 34, 35, 36, 37] have analyzed the more recent available redshift surveys using N(r) or related measures with appropriate estimators. Their results show unambiguously an increasing trend of D₂ with the scale from values of D₂ ~ 2 at intermediate scales to values of D₂ ~ 3 at scales larger than 30 h^-1 Mpc. Moreover, one of the strong predictions of the fractal hypothesis is that the correlation length - the value r₀ at which the correlation function reaches the unity ((r₀) = 1) - must increase linearly with the depth of the sample. This seems not to be the case [38, 39].