2. THEORY

The currently accepted paradigm describing our homogeneous and isotropic Universe is based on the Robertson-Walker metric

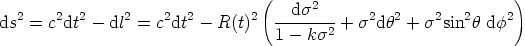(1)

and Einstein's covariant formula for the law of gravitation,

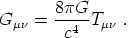(2)

In Eq. (1) ds is the line element in four-dimensional spacetime, t is the time, R(t) is the cosmic scale, is the comoving distance as measured by an observer who follows the expansion, k is the curvature parameter, c is the velocity of light, and , are comoving angular coordinates. In Eq. (2) G_µ is the Einstein tensor describing the curved geometry of spacetime, T_µ is the energy-momentum tensor, and G is Newton's constant.

From these equations one derives Friedmann's equations which can be put into the form

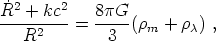(3)

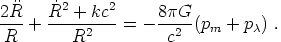(4)

Here are energy densities, the subscripts m and refer to matter and cosmological constant (or dark energy), respectively; p_m and p are the corresponding pressures of matter and dark energy, respectively. Using the expression for the critical density today,

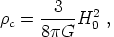(5)

where H₀ is the Hubble parameter at the present time, one can define density parameters for each energy component by

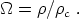(6)

The total density parameter is

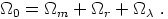(7)

In what follows we shall ignore the very small radiation density parameter _r. The matter density parameter _m can further be divided into a cold dark matter (CDM) component _CDM, a baryonic component _b and a neutrino component .

The pressure of matter is certainly very small, otherwise one would observe the galaxies having random motion similar to that of molecules in a gas under pressure. Thus one can set p_m = 0 in Eq. (4) to a good approximation. If the expansion is adiabatic so that the pressure of dark energy can be written in the form

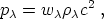(8)

and if dark energy and matter do not transform into one another, conservation of dark energy can be written

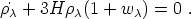(9)

One further parameter is the deceleration parameter q₀, defined by

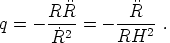(10)

Eliminating 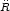between Eqs. (4) and (10) one can see that q₀ is not an independent parameter.

The curvature parameter k in Eqs. (1), (3) and (4) describes the geometry of space: a spatially open universe is defined by k = -1, a closed universe by k = + 1 and a flat universe by k = 0. The curvature parameter is not an observable, but it is proportional to ₀ - 1, so if ₀ is observed to be 1, the Universe is spatially flat.