3. THE HUBBLE PARAMETER

From the definition of the Hubble parameter H = 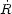/ R one sees that it has the dimension of inverse time. Thus a characteristic time scale for the expansion of the Universe is the Hubble time

(11)

Here h is the commonly used dimensionless quantity

(12)

The Hubble parameter also determines the size scale of the observable Universe. In time _H, radiation travelling with the speed of light has reached the Hubble radius

(13)

Or, to put it differently, according to Hubble's non-relativistic law,

(14)

objects at this distance would be expected to attain the speed of light which is an absolute limit in the theory of special relativity. However, in special relativity the redshift z is infinite for objects at distance r_H receding with the speed of light and thus unphysical. Therefore no information can reach us from farther away, all radiation is redshifted to infinite wavelengths and no particle emitted within the Universe can exceed this distance.

Our present knowledge of H₀ comes from the Hubble Space Telescope (HST) Key Project [9]. The goal of this project was to determine H₀ by a Cepheid calibration of a number of independent, secondary distance indicators, including Type Ia supernovae, the Tully-Fisher relation, the fundamental plane for elliptical galaxies, surface brightness fluctuations, and type II supernovae. Here we shall restrict the discussion to the best absolute determinations of H₀, which are those from supernovæ of type Ia.

Visible bright supernova explosions are very brief events (one month) and very rare, historical records show that in our Galaxy they have occurred only every 300 years. The most recent one occurred in 1987 (code name SN1987A), not exactly in our Galaxy but in the nearby Large Magellanic Cloud (LMC). Since it now has become possible to observe supernovæ in very distant galaxies, one does not have to wait 300 years for the next one.

The physical reason for this type of explosion (type SNII supernova) is the accumulation of Fe-group elements at the core of a massive red giant star of size 8-200 M which already has burned its hydrogen, helium and other light elements. Another type of explosion (type SNIa supernova) occurs when a degenerate dwarf star of CNO composition enters a stage of rapid nuclear burning to Fe-group elements.

The SNIa is the brightest and most homogeneous class of supernovæ with hydrogen-poor spectra, their peak brightness can serve as remarkably precise standard candles visible from very far. Additional information is provided by the colour, the spectrum, and an empirical correlation observed between the time scale of the sharply rising light curve and the peak luminosity, which is followed by a gradual decline. Although supernovæ are difficult to find, they can be used to determine H₀ out to great distances, 500 Mpc or z 0.1, and the internal precision of the method is very high. At greater distances one can still find supernovæ, but Hubble's linear law (14) is then no longer valid, the velocity starts to accelerate.

Supernovæ of type II are fainter, and show a wider variation in luminosity. Thus they are not standard candles, but the time evolution of their expanding atmospheres provides an indirect distance indicator, useful out to some 200 Mpc.

Two further methods to determine H₀ make use of correlations between different galaxy properties. Spiral galaxies rotate, and there the Tully-Fisher relation correlates total luminosity with maximum rotation velocity. This is currently the most commonly applied distance indicator, useful for measuring extragalactic distances out to about 150 Mpc. Elliptical galaxies do not rotate, they are found to occupy a "fundamental plane" in which an effective radius is tightly correlated with the surface brightness inside that radius and with the central velocity dispersion of the stars. In principle this method could be applied out to z 1, but in practice stellar evolution effects and the non-linearity of Hubble's law limit the method to z 0.1, or about 400 Mpc.

The resolution of individual stars within galaxies clearly depends on the distance to the galaxy. This method, called surface brightness fluctuations (SBF), is an indicator of relative distances to elliptical galaxies and some types of spirals. The internal precision of the method is very high, but it can be applied only out to about 70 Mpc.

Observations from the HST combining all this methods [9] and independent SNIa observations from observatories on the ground [26] agree on a value

(15)

Note that the second error in Eq. (15) which is systematical, is much bigger than the statistical error. This illustrates that there are many unknown effects which complicate the determination of H₀, and which in the past have made all determinations controversial. To give just one example, if there is dust on the sight line to a supernova, its light would be reddened and one would conclude that the recession velocity is higher than it in reality is. There are other methods such as weak lensing which do not suffer from this systematic error, but they have not yet reached a precision superior to that in Eq. (15).