3. DARK MATTER: BOUND TO GALAXIES OR SMOOTHLY DISTRIBUTED?

Given that the total masses of clusters like Coma greatly exceed their luminous masses - although by amounts that are still fairly uncertain - it is natural to wonder whether the d dark matter is bound to the bright galaxies (in the form of massive halos, say) or whether it is more smoothly distributed. Here it is important to remember that there is currently no strong evidence for massive halos around "hot" stellar systems, and thus no reason to assume that the cluster dark matter is bound to galaxies, most of which are elliptical. The fraction of cluster mass that is associated with galaxies has important consequences for the rate of galaxy-galaxy interactions and orbital decay (see below). One of the first attempts to deal with this question was made by Noonan (1970), who noted that the tidal field produced by the potential well of a cluster might be sufficiently strong to pull luminous matter (along with, presumably, any dark-matter halos) from the brightest galaxies. Noonan's hypothesis has been unaccountably neglected; most subsequent work has focused instead on collisions as the physical process that determines galaxy masses in clusters.

There are two major sources of uncertainty that make it difficult to assess the importance of Noonan's tidal truncation hypothesis. 1. As discussed above, neither the (macroscopic) distribution of the cluster dark matter, nor the distribution of galaxy orbits, is well constrained, even in the best-observed clusters like Coma. 2. Although simple tidal theory makes a definite prediction about the limiting radius of a galaxy, with specified mass, as it orbits about a potential center, it says essentially nothing about the tidally-limited mass itself. This is because the total mass depends strongly on the distribution of matter near the galaxy's Lagrangian radius, and this distribution is essentially unknown. A straightforward analysis gives a feeling for the uncertainties involved. Consider a galaxy orbiting at a fixed radius r₀ from the center of a cluster. The equations of motion, in the rotating frame, of a star that remains close to the galaxy in the plane of its orbit are

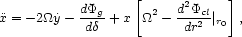(11a)

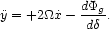(11b)

Here 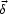= (x, y) is the position of the star relative to the galaxy center, with x parallel to the orbital radius vector r₀; _g() and _cl(r) are the galaxy and cluster potentials, respectively; and is the angular frequency of the galaxy orbit. Neglecting Coriolis terms, equation (11a) predicts that a star would feel a zero net force at the Lagrangian radius _L, where _L[² - (d² _cl / dr²)_r0] = (d_g / d)_L. In order to derive a tidally-truncated mass from this equation, we need to assume some relation between the (truncated) mass mg and the tidal radius r_t of the galaxy. Suppose that Gm_g = ² _g² r_t / 2, where _g is the galaxy central velocity dispersion, and is an unknown parameter that specifies the shape of the halo density profile. If the dark matter producing the tidal field is distributed roughly "isothermally" near the cluster center, with central density ₀, then ² d² _cl / dr² G ₀, and

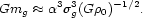(12)

A more careful calculation would give a value (dependent on orbital parameters) for the undetermined coefficient in equation (12). Note, however, that the predicted mass depends sensitively on the unknown structural parameter . If the halo of the tidally truncated galaxy has the same mass distribution as an isotropic Michie-King model of high central concentration - a natural assumption, given that these models look so much like globular clusters, which are thought to be tidally truncated - then 1. But even along the Michie-King sequence of models, a oscillates between ~ 0.85 and ~ 1.3, giving an uncertainty of nearly a factor of four to the predicted mass. Other reasonable families of models (eg. Wilson [1975] spheres) have halos that look very different. Thus, simple tidal theory can give only an order-ofmagnitude indication of the mass that could remain bound to a galaxy in a cluster, even a cluster with a known potential.

Figure 4. Tidally-truncated masses, in units of G-1 g3(G 0)-1/2, of galaxies orbiting in a cluster with potential given by eqn. (13). Lower panel: minitial = 2; upper panel: minitial = 3. Rapo: orbital apocenter; Rperi: orbital pericenter.

The only way to reduce this uncertainty is to simulate the tidal truncation process via an N-body code. Figure 4 shows the final masses of model galaxies, containing 2000 particles initially, after orbiting for a time ~ 40(G ₀)^-1/2 about the center of a cluster with mass density

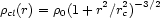(13)

(see Merritt and White 1987 for a description of the technique). For Zwicky's Coma model, ₀ 1 × 10^-2h² M pc^-3, making the simulated evolution time ~ 7 × 10⁹ h^-1 years. According to Figure 4, galaxies on elongated, high-energy orbits are the most strongly truncated, although the dependence of final mass on orbital parameters is not great. Final masses of galaxies with pericenters near r_c (the dark matter "core radius") are given approximately by

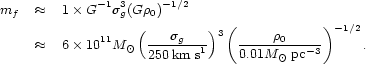(14)

Detailed examination of the final states of these "truncated galaxies" reveals that they contain about four times as much mass within their tidal radii as do = 1 Michie-King models. The final tidal and half-mass radii are

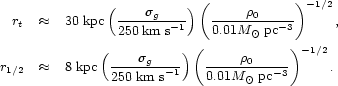(15)

Equation (14) predicts that a bright galaxy orbiting near the center of the Coma cluster could indeed retain a fairly massive halo, similar in mass to the halos of bright spiral galaxies, as long as the central density of dark matter in Coma is not much greater than in Zwicky's model. Furthermore, equations (15) imply that little if any luminous matter would be tidally removed, since characteristic luminous radii of bright elliptical galaxies are 5h^-1 kpc. Thus tidal truncation is probably not a viable mechanism for producing the "diffuse light" that is thought to be present in some clusters, including Coma (e.g. Thuan and Kormendy 1977). Both of these conclusions would have to be modified if cluster central densities could be shown to be much higher than in Zwicky's model. High central densities are likely in clusters containing "cD" galaxies, especially if the cD's are themselves surrounded by supermassive dark halos. This point is discussed further in the next section.

Finally, we can estimate the total fraction of the dark matter in Coma that could remain bound to galaxies in a model like Zwicky's. If we assume a Schechter (1976) galaxy luminosity function N(L)dL (L / L^*)^-1 exp(- L / L^*) d (L / L^*), and furthermore that the velocity dispersion of the halo material scales with the luminosity of its parent galaxy as _g 225 km s^-1 (L / L^*)^1/4, then equation (14) predicts that a fraction

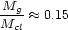(16)

of the Coma cluster's mass should reside in galaxies. This estimate is an upper limit in the sense that it neglects the (probably greater, but transient) tidal stresses during cluster formation, galaxy-galaxy collisions, etc. It suggests that almost all of the dark matter in rich clusters is smoothly distributed.