10.1. Limits to the neutrino mass
Even though a CDM-dominated universe matches the
data very well, there are many plausible variations
to consider. Probably the most interesting is the
neutrino mass: experimental data on neutrino
oscillations mean that at least one neutrino must have a mass of
0.05 eV, so that
10-3 -
the same order of magnitude as stellar mass.
As explained in earlier, a non-zero neutrino mass can
lead to relatively enhanced large-scale power, beyond the
neutrino free-streaming scale. This is illustrated in
figure 21, taken from
Elgaroy et al. (2002).
Broadly speaking, allowing a significant neutrino mass
changes the spectrum in a way that resembles lower density,
so there is a near-degeneracy between neutrino mass fraction and
mh
(figure 21). A limit on the neutrino
fraction thus requires a prior on
mh.
Based on the cluster baryon fraction plus BBN, Elgaroy et al. adopt
m <
0.5; together with the HST
Hubble constant, this yields a marginalized 95% limit of
f < 0.13, or
m < 1.8 eV.
Note that this is the sum of the eigenvalues of the mass matrix:
given neutrino oscillation results (e.g.
Ahmad et al. 2002;
Eguchi et al. 2003),
the only way a cosmologically
significant density can arise is via a nearly degenerate
hierarchy, so this allows us to deduce
m < 0.6 eV
for any one species. Including the latest WMAP results in
order to set a more strict limit on
mh, this limit falls to 0.23 eV
(Spergel et al. 2003).
 |
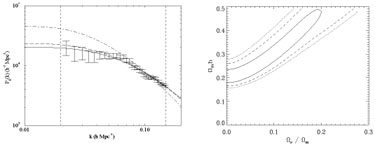Figure 21. Results from
Elgaroy et al. (2002),
who considered constraints on the neutrino mass from 2dFGRS.
The first panel shows Power spectra for
|
=
0.7, h = 0.7,
