9.1. Matter fluctuation amplitude and bias
The above conclusions were obtained by considering the shapes
of the CMB and galaxy power spectra. However, it is also of
great interest to consider the amplitude of mass fluctuations,
since a comparison with the galaxy power spectrum
allows us to infer the degree of bias directly.
This analysis was performed by
Lahav et al. (2002).
Given assumed values for the cosmological parameters, the
present-day linear normalization of the mass spectrum (e.g.
8)
can be inferred. It is convenient to define a corresponding measure
for the galaxies,
8g, such that
we can express the bias parameter as
 |
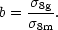(161) |
In practice, we define
8g to be the
value required
to fit a CDM model to the power-spectrum data on linear scales (0.02
< k < 0.15 h Mpc-1).
The amplitude of 2dFGRS galaxies in real space estimated by
Lahav et al. (2002) is
8gR(L*) =
0.76, with a negligibly small random error.
This assumes no evolution in
8g,
plus the luminosity dependence of clustering measured by
Norberg et al. (2001).
The value of
8 for the
dark matter can be deduced from the CMB fits.
Percival et al. (2002)
obtain
 |
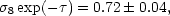(162) |
where the error bar includes both data errors and theory
uncertainty. The WMAP number here is almost identical:
8
exp(- 
) = 0.71, but no error
is quoted
(Spergel et al. 2003).
The unsatisfactory feature is the degeneracy
with the optical depth to last scattering. For reionization
at redshift 8, we would have
0.05;
it is not expected theoretically that
can be hugely larger,
and popular models would place reionization between z = 10 and
z = 15, or
0.1 (e.g.
Loeb & Barkana 2001).
One of the many impressive aspects of the WMAP results is
that they are able to infer
= 0.17± 0.04 from
large-scale polarization. Taken at face value,
= 0.17 would argue for
reionization at z = 20, but the error means that more
conventional figures are far from being ruled out.
Taking all this together, it seems reasonable to assume that
the true value of
8 is within a
few % of 0.80. Given the 2dFGRS figure of
8gR
= 0.76,
this implies that L* galaxies are very nearly
exactly unbiased. Since there are substantial variations
in the clustering amplitude with galaxy type, this outcome
must be something of a coincidence. This conclusion of near-unity bias
was reinforced in a completely independent way, by using the
measurements of the bispectrum of galaxies in the 2dFGRS
(Verde et al. 2002).
As it is based on three-point correlations, this statistic is sensitive
to the filamentary nature of the galaxy distribution - which is a
signature of nonlinear evolution. One can therefore split the
degeneracy between the amplitude of dark-matter fluctuations and the
amount of bias.
These conclusions point the way towards a possible limit on the
tensor contribution: a large contribution of tensors to the COBE
signal would lower the required scalar amplitude. As an extreme
example, a scalar-to-tensor ratio of 1 would reduce the
`apparent' 8
by roughly a factor of 21/2, to 0.5. Even
for an implausibly large value of
, this would be hard
to reconcile with the level of galaxy clustering plus the
requirement of a low degree of bias. Also, more direct limits
on 8 are now
being derived from large-scale gravitational lensing surveys, with
8
0.7 to 0.8 being favoured
(e.g. Brown et al. 2003;
Jarvis et al. 2003).