2. Newtonian equations of motion

2.1. Matter-dominated universe

In the Newtonian approach, we treat dynamics of cosmological matter exactly as we would in the laboratory, by finding the equations of motion induced by either pressure or gravity. In what follows, it should be remembered that we probably need to deal in practice with two rather different kinds of material: dark matter that is collisionless and interacts only via gravity, and baryonic material which is a collisional fluid, coupled to dark matter only via gravity (and to photons via Thomson scattering, so that the dominant part of the pressure derives from the radiation).

Also, the problem of cosmological dynamics has to deal with the characteristic feature of the Hubble expansion. This means that it is convenient to introduce comoving length units, and to consider primarily peculiar velocities - i.e. deviations from the Hubble flow. The standard notation that includes these aspects is

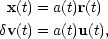(7)

so that x has units of proper length, i.e. it is an Eulerian coordinate. First note that the comoving peculiar velocity u is just the time derivative of the comoving coordinate r:

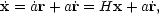(8)

where the rhs must be equal to the Hubble flow Hx, plus the peculiar velocity v = a u. In this equation, dots stand for exact convective time derivatives - i.e. time derivatives measured by an observer who follows a particle's trajectory - rather than partial time derivatives / t.

The equation of motion follows from writing the Eulerian equation of motion as 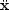= g₀ + g, where g = - / a is the peculiar acceleration, and g₀ is the acceleration that acts on a particle in a homogeneous universe (neglecting pressure forces to start with, for simplicity). Differentiating x = a r twice gives

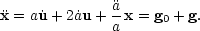(9)

The unperturbed equation corresponds to zero peculiar velocity and zero peculiar acceleration: ( / a) x = g₀; subtracting this gives the perturbed equation of motion

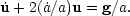(10)

The only point that needs a little more thought is the nature of the unperturbed equation of motion. This cannot be derived from Newtonian gravity alone, since general relativity is really needed for a proper derivation of the homogeneous equation of motion. However, as long as we are happy to accept that g₀ is given, then it is a well-defined procedure to add a peculiar acceleration that is the gradient of the potential derived from the density perturbations.

The equation of motion for the peculiar velocity shows that u is affected by gravitational acceleration and by the Hubble drag term, 2( / a)u. This arises because the peculiar velocity falls with time as a particle attempts to catch up with successively more distant (and therefore more rapidly receding) neighbours. If the proper peculiar velocity is v, then after time dt the galaxy will have moved a proper distance x = v dt from its original location. Its near neighbours will now be galaxies with recessional velocities H x = H v dt, relative to which the peculiar velocity will have fallen to v - Hx. The equation of motion is therefore just

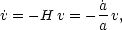(11)

with the solution v a^-1: peculiar velocities of nonrelativistic objects suffer redshifting by exactly the same factor as photon momenta. This becomes 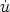= - 2H u when rewritten in comoving units.

The peculiar velocity is directly related to the evolution of the density field, through conservation of mass. This is expressed via the continuity equation, which takes the form

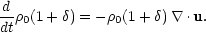(12)

Here, spatial derivatives are with respect to comoving coordinates:

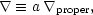(13)

which we will assume hereafter, and the time derivative is once more a convective one:

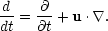(14)

Finally, when using comoving length units, the background density ₀ independent of time, and so the full continuity equation can be written as

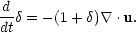(15)

Unlike the equation of motion for u, this is not linear in the perturbations and u. To cure this, we restrict ourselves to the case << 1 and linearize the equation, neglecting second-order terms like × u, which removes the distinction between convective and partial time derivatives. The linearized equations for conservation of momentum and matter as experienced by fundamental observers moving with the Hubble flow are then:

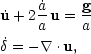(16)

where the peculiar gravitational acceleration - / a is denoted by g.

The solutions of these equations can be decomposed into modes either parallel to g or independent of g (these are the homogeneous and inhomogeneous solutions to the equation of motion). The homogeneous case corresponds to no peculiar gravity - i.e. zero density perturbation. This is consistent with the linearized continuity equation, ^. u = - 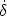, which says that it is possible to have vorticity modes with ^. u = 0 for which 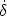vanishes, so there is no growth of structure in this case. The proper velocities of these vorticity modes decay as v = au a^-1, as with the kinematic analysis for a single particle.

Growing mode     For the growing mode, it is most convenient to eliminate u by taking the divergence of the equation of motion for u, and the time derivative of the continuity equation. This requires a knowledge of ^. g, which comes via Poisson's equation: ^. g = 4 Ga ₀ . The resulting 2nd-order equation for is

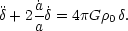(17)

This is easily solved for the _m = 1 case, where 4 G ₀ = 3H² / 2 = 2/3 t², and a power-law solution works:

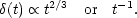(18)

The first solution, with (t) a(t) is the growing mode, corresponding to the gravitational instability of density perturbations. Given some small initial seed fluctuations, this is the simplest way of creating a universe with any desired degree of inhomogeneity.

An alternative way of looking at the growing mode is that we want to try looking for a homogeneous solution u = F(t)g. Then using continuity plus ^. g = 4 Ga ₀ , gives us

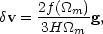(19)

where the function f (_m) d ln / d ln a. A very good approximation to this (Peebles 1980) is f ^0.6 (a result that is almost independent of ; Lahav et al. 1991).

Jeans scale     So far, we have mainly considered the collisionless component. For the photon-baryon gas, all that changes is that the peculiar acceleration gains a term from the pressure gradients:

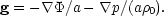(20)

The pressure fluctuations are related to the density perturbations via the sound speed

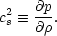(21)

Now think of a plane-wave disturbance e^{-ik . r}, where k is a comoving wavevector; in other words, suppose that the wavelength of a single Fourier mode stretches with the universe. All time dependence is carried by the amplitude of the wave, and so the spatial dependence can be factored out of time derivatives in the above equations (which would not be true with a constant comoving wavenumber k / a). The equation of motion for then gains an extra term on the rhs from the pressure gradient:

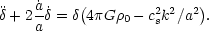(22)

This shows that there is a critical proper wavelength, the Jeans length, at which we switch from the possibility of gravity-driven growth for long-wavelength modes to standing sound waves at short wavelengths. This critical length is

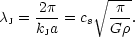(23)

Qualitatively, we expect to have no growth when the `driving term' on the rhs is negative. However, owing to the expansion, _J will change with time, and so a given perturbation may switch between periods of growth and stasis. These effects help to govern the form of the perturbation spectrum that propagates to the present universe from early times.

The general case     How does the matter-dominated growth (a) a change at late times when _m 1? The differential equation for is as before, but a(t) is altered. Provided the vacuum equation of state is exactly p = - c², or if the vacuum energy is negligible, the solutions to the growth equations can be written as

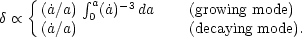(24)

(Heath 1977; see also section 10 of Peebles 1980). For the most general case, e.g. a vacuum with time-varying density, these do not apply, and the differential equation for must be integrated directly.

In any case, the equation for the growing mode requires numerical integration unless the vacuum energy vanishes. A very good approximation to the answer is given by Carroll et al. (1992):

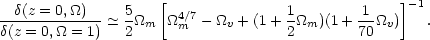(25)

This fitting formula for the growth suppression in low-density universes is an invaluable practical tool. For flat models with _m + _v = 1, it says that the growth suppression is less marked than for an open universe - approximately ^0.23 as against ^0.65 in the = 0 case. This reflects the more rapid variation of _v with redshift; if the cosmological constant is important dynamically, this only became so very recently, and the universe spent more of its history in a nearly Einstein-de Sitter state by comparison with an open universe of the same _m.