2.2. Radiation-dominated universe

At early enough times, the universe was radiation dominated (c_s = c / 3^1/2) and the analysis so far does not apply. It is common to resort to general relativity perturbation theory at this point. However, the fields are still weak, and so it is possible to generate the results we need by using special relativity fluid mechanics and Newtonian gravity with a relativistic source term:

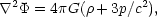(26)

in Eulerian units. The main change from the previous treatment come from factors of 2 and 4/3 due to this ( +3p / c²) term, and other contributions of the pressure to the relativistic equation of motion. The resulting evolution equation for is

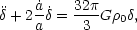(27)

so the net result of all the relativistic corrections is a driving term on the rhs that is a factor 8/3 higher than in the matter-dominated case (see e.g. Section 15.2 of Peacock 1999 for the details).

In both matter- and radiation-dominated universes with = 1, we have ₀ 1/t²:

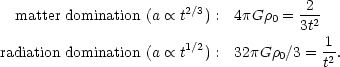(28)

Every term in the equation for is thus the product of derivatives of and powers of t, and a power-law solution is obviously possible. If we try tⁿ, then the result is n = 2/3 or -1 for matter domination; for radiation domination, this becomes n = ± 1. For the growing mode, these can be combined rather conveniently using the conformal time dt / a:

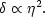(29)

The quantity is proportional to the comoving size of the cosmological particle horizon.

One further way of stating this result is that gravitational potential perturbations are independent of time (at least while = 1). Poisson's equation tells us that - k² / a² ; since a^-3 for matter domination or a^-4 for radiation, that gives / a or / a² respectively, so that is independent of a in either case. In other words, the metric fluctuations resulting from potential perturbations are frozen, at least for perturbations with wavelengths greater than the horizon size.