2.5. Transfer functions and characteristic scales

The transfer function for models with the full above list of ingredients was first computed accurately by Bond & Szalay (1983), and is today routinely available via public-domain codes such as CMBFAST (Seljak & Zaldarriaga 1996). These calculations are a technical challenge because we have a mixture of matter (both collisionless dark particles and baryonic plasma) and relativistic particles (collisionless neutrinos and collisional photons), which does not behave as a simple fluid. Particular problems are caused by the change in the photon component from being a fluid tightly coupled to the baryons by Thomson scattering, to being collisionless after recombination. Accurate results require a solution of the Boltzmann equation to follow the evolution in detail.

Figure 2. A plot of transfer functions for various adiabatic models, in which Tk 1 at small k. A number of possible matter contents are illustrated: pure baryons; pure CDM; pure HDM. For dark-matter models, the characteristic wavenumber scales proportional to m h2, marking the break scale corresponding to the horizon length at matter-radiation equality. The scaling for baryonic models does not obey this exactly; the plotted case corresponds to m = 1, h = 0.5.

Some illustrative results are shown in figure 2. Leaving aside the isocurvature models, all adiabatic cases have T 1 on large scales - i.e. there is growth at the universal rate (which is such that the amplitude of potential perturbations is constant until the vacuum starts to be important at z 1). The different shapes of the functions can be understood intuitively in terms of a few special length scales, as follows:

(1) Horizon length at matter-radiation equality. The main bend visible in all transfer functions is due to the Mészáros effect, which arises because the universe is radiation dominated at early times. Fluctuations in the matter can only grow if dark matter and radiation fall together. This does not happen for perturbations of small wavelength, because photons and matter can separate. Growth only occurs for perturbations of wavelength larger than the horizon distance, where there has been no time for the matter and radiation to separate. The relative diminution in fluctuations at high k is the amount of growth missed out on between horizon entry and z_eq, which would be D_H² in the absence of the Mészáros effect. Perturbations with larger k enter the horizon when D_H 1/k; they are then frozen until z_eq, at which point they can grow again. The missing growth factor is just the square of the change in D_H during this period, which is k². The approximate limits of the CDM transfer function are therefore

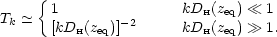(45)

This process continues, until z_eq = 23 900 _m h², where the universe becomes matter dominated. We therefore expect a characteristic `break' in the fluctuation spectrum around the comoving horizon length at this time. Using a distance-redshift relation that ignores vacuum energy at high z,

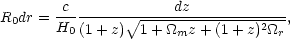(46)

we obtain

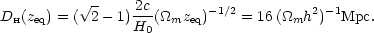(47)

Since distances in cosmology always scale as h^-1, this means that _m h should be observable.

(2) Free-streaming length. This relatively gentle filtering away of the initial fluctuations is all that applies to a universe dominated by Cold Dark Matter, in which random velocities are negligible. A CDM universe thus contains fluctuations in the dark matter on all scales, and structure formation proceeds via hierarchical process in which nonlinear structures grow via mergers.

Examples of CDM would be thermal relic WIMPs with masses of order 100 GeV. Relic particles that were never in equilibrium, such as axions, also come under this heading, as do more exotic possibilities such as primordial black holes. A more interesting case arises when thermal relics have lower masses. For collisionless dark matter, perturbations can be erased simply by free streaming: random particle velocities cause blobs to disperse. At early times (kT > mc²), the particles will travel at c, and so any perturbation that has entered the horizon will be damped.This process switches off when the particles become non-relativistic, so that perturbations are erased up to proper lengthscales of ct(kT = mc²). This translates to a comoving horizon scale (2ct / a during the radiation era) at kT = mc² of

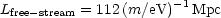(48)

(in detail, the appropriate figure for neutrinos will be smaller by (4/11)^1/3 since they have a smaller temperature than the photons). A light neutrino-like relic that decouples while it is relativistic satisfies

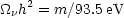(49)

Thus, the damping scale for HDM (Hot Dark Matter) is of order the bend scale. Alternatively, if the particle decouples sufficiently early, its relative number density is boosted by annihilations, so that the critical particle mass to make _m = 1 can be boosted to around 1-10 keV (Warm Dark Matter). The existence of galaxies at z 6 tells us that the coherence scale must have been below about 100 kpc, so WDM is close to being ruled out. A similar constraint is obtained from small-scale structure in the Lyman-alpha forest (Narayanan et al. 2000): m > 0.75 keV.

A more interesting (and probably practically relevant) case is when the dark matter is a mixture of hot and cold components. The free-streaming length for the hot component can therefore be very large, but within range of observations. The dispersal of HDM fluctuations reduces the CDM growth rate on all scales below L_free-stream - or, relative to small scales, there is an enhancement in large-scale power.

(3) Acoustic horizon length. The horizon at matter-radiation equality also enters in the properties of the baryon component. Since the sound speed is of order c, the largest scales that can undergo a single acoustic oscillation are of order the horizon. The transfer function for a pure baryon universe shows large modulations, reflecting the number of oscillations that have been completed before the universe becomes matter dominated and the pressure support drops. The lack of such large modulations in real data is one of the most generic reasons for believing in collisionless dark matter. Acoustic oscillations persist even when baryons are subdominant, however, and can be detectable as lower-level modulations in the transfer function (e.g. Goldberg & Strauss 1998; Meiksin et al. 1999).

(4) Silk damping length. Acoustic oscillations are also damped on small scales, where the process is called Silk damping: the mean free path of photons due to scattering by the plasma is non-zero, and so radiation can diffuse out of a perturbation, convecting the plasma with it. The typical distance of a random walk in terms of the diffusion coefficient D is x Dt^1/2, which gives a damping length of

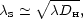(51)

the geometric mean of the horizon size and the mean free path. Since = 1 / (n _T) = 44.3(1 + z)^-3(_b h²)^-1 proper Gpc, we obtain a comoving damping length of

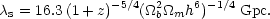(52)

This becomes close to the horizon length by the time of last scattering, 1 + z 1100. The resulting damping effect can be seen in figure 2 k ~ 10k_H.

Fitting formulae     It is invaluable in practice to have some accurate analytic formulae that fit the numerical results for transfer functions. We give below results for some common models of particular interest (illustrated in figure 2 along with other cases where a fitting formula is impractical). For the models with collisionless dark matter, _b << _m is assumed, so that all lengths scale with the horizon size at matter-radiation equality, leading to the definition

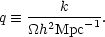(52)

We consider the following cases: (1) Adiabatic CDM; (2) Adiabatic massive neutrinos (1 massive, 2 massless); (3) Isocurvature CDM; these expressions come from Bardeen et al. (1986; BBKS). Since the characteristic length-scale in the transfer function depends on the horizon size at matter-radiation equality, the temperature of the CMB enters. In the above formulae, it is assumed to be exactly 2.7 K; for other values, the characteristic wavenumbers scale T^-2. For these purposes massless neutrinos count as radiation, and three species of these contribute a total density that is 0.68 that of the photons.

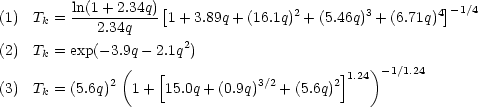(53)

The case of mixed dark matter (MDM: a mixture of massive neutrinos and CDM) is more complex. Ma (1996) gives the following expression:

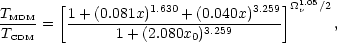(54)

where x k / , a^1/2 h² and x₀ is the value of x at a = 1. The scale-factor dependence is such that the damping from neutrino free-streaming is less severe at high redshift, but the spectrum is very nearly of constant shape for z 10. See Pogosyan & Starobinsky (1995) for a more complicated fit of higher accuracy.

These expressions are useful for work at a level of 10% precision, but increasingly it is necessary to do better. In particular, these expressions do not include the weak oscillatory features that are expected if the universe has a significant baryon content. Eisenstein & Hu (1998) give an accurate (but long) fitting formula that describes these wiggles for the CDM transfer function. This was extended to cover MDM in Eisenstein & Hu (1999).