5.2. The 2dFGRS power spectrum and CDM models

Perhaps the key aim of the 2dFGRS was to perform an accurate measurement of the 3D clustering power spectrum, in order to improve on the APM result, which was deduced by deprojection of angular clustering (Baugh & Efstathiou 1993, 1994). The results of this direct estimation of the 3D power spectrum are shown in figure 5 (Percival et al. 2001). This power-spectrum estimate uses the FFT-based approach of Feldman, Kaiser & Peacock (1994), and needs to be interpreted with care. Firstly, it is a raw redshift-space estimate, so that the power beyond k 0.2 h Mpc^-1 is severely damped by smearing due to peculiar velocities, as well as being affected by nonlinear evolution. Finally, the FKP estimator yields the true power convolved with the window function. This modifies the power significantly on large scales (roughly a 20% correction). An approximate correction for this has been made in figure 5.

Figure 5. The 2dFGRS redshift-space dimensionless power spectrum, 2(k), estimated according to the FKP procedure. The solid points with error bars show the power estimate. The window function correlates the results at different k values, and also distorts the large-scale shape of the power spectrum An approximate correction for the latter effect has been applied. The solid and dashed lines show various CDM models, all assuming n = 1. For the case with non-negligible baryon content, a big-bang nucleosynthesis value of b h2 = 0.02 is assumed, together with h = 0.7. A good fit is clearly obtained for m h 0.2. Note that the observed power at large k will be boosted by nonlinear effects, but damped by small-scale random peculiar velocities. It appears that these two effects very nearly cancel, but model fitting is generally performed only at k < 0.15 h Mpc -1 in order to avoid these complications.

The fundamental assumption is that, on large scales, linear biasing applies, so that the nonlinear galaxy power spectrum in redshift space has a shape identical to that of linear theory in real space. This assumption is valid for k < 0.15 h Mpc^-1; the detailed justification comes from analyzing realistic mock data derived from N-body simulations (Cole et al. 1998). The free parameters in fitting CDM models are thus the primordial spectral index, n, the Hubble parameter, h, the total matter density, _m, and the baryon fraction, _b / _m. Note that the vacuum energy does not enter. Initially, we show results assuming n = 1; this assumption is relaxed later.

An accurate model comparison requires the full covariance matrix of the data, because the convolving effect of the window function causes the power at adjacent k values to be correlated. This covariance matrix was estimated by applying the survey window to a library of Gaussian realisations of linear density fields, and checked against a set of mock catalogues. It is now possible to explore the space of CDM models, and likelihood contours in _b / _m versus _mh are shown in figure 6. At each point in this surface we have marginalized by integrating the likelihood surface over the two free parameters, h and the power spectrum amplitude. We have added a Gaussian prior h = 0.7± 10%, representing external constraints such as the HST key project (Freedman et al. 2001); this has only a minor effect on the results.

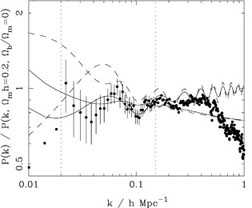Figure 6. Likelihood contours for the best-fit linear CDM fit to the 2dFGRS power spectrum over the region 0.02 < k < 0.15. Contours are plotted at the usual positions for one-parameter confidence of 68%, and two-parameter confidence of 68%, 95% and 99% (i.e. -2 ln( / max) = 1, 2.3, 6.0, 9.2). We have marginalized over the missing free parameters (h and the power spectrum amplitude). A prior on h of h = 0.7± 10% was assumed. This result is compared to estimates from X-ray cluster analysis (Evrard 1997) and big-bang nucleosynthesis (Burles et al. 2001). The second panel shows the 2dFGRS data compared with the two preferred models from the Maximum Likelihood fits convolved with the window function (solid lines). The unconvolved models are also shown (dashed lines). The m h 0.6, b / m = 0.42, h = 0.7 model has the higher bump at k 0.05 h Mpc-1. The smoother m h 0.20, b / m = 0.15, h = 0.7 model is a better fit to the data because of the overall shape. A preliminary analysis of the complete final 2dFGRS sample yields a slightly smoother spectrum than the results shown here (from Percival et al. 2001), so that the high-baryon solution becomes disfavoured.

Figure 6 shows that there is a degeneracy between _m h and the baryonic fraction _b / _m. However, there are two local maxima in the likelihood, one with _m h 0.2 and ~ 20% baryons, plus a secondary solution _m h 0.6 and ~ 40% baryons. The high-density model can be rejected through a variety of arguments, and the preferred solution is

(95)

The 2dFGRS data are compared to the best-fit linear power spectra convolved with the window function in figure 6. The low-density model fits the overall shape of the spectrum with relatively small `wiggles', while the solution at _m h 0.6 provides a better fit to the bump at k 0.065 h Mpc^-1, but fits the overall shape less well. A preliminary analysis of P(k) from the full final dataset shows that P(k) becomes smoother: the high-baryon solution becomes disfavoured, and the uncertainties narrow slightly around the lower-density solution: _m h = 0.18± 0.02; _b / _m = 0.17± 0.06. The lack of large-amplitude oscillatory features in the power spectrum is one general reason for believing that the universe is dominated by collisionless nonbaryonic matter. In detail, the constraints on the collisional nature of dark matter are weak, since all we require is that the effective sound speed for modes of 100-Mpc wavelength is less than about 0.1c. Nevertheless, if a pure-baryon model is ruled out, the next simplest alternative would arguably be to introduce a weakly-interacting relic particle, so there is at least circumstantial evidence in this direction from the power spectrum.

It is interesting to compare these conclusions with other constraints. These are shown on figure =, again assuming h = 0.7± 10%. Estimates of the Deuterium to Hydrogen ratio in QSO spectra combined big-bang nucleosynthesis theory predict _b h² = 0.020 ± 0.001 (Burles et al. 2001), which translates to the shown locus of f_b vs _m h. X-ray cluster analysis yields a baryon fraction _b / _m = 0.127 ± 0.017 (Evrard 1997) which is within 1 of our value. These loci intersect very close to our preferred model.

Perhaps the main point to emphasise here is that the 2dFGRS results are not greatly sensitive to the assumed tilt of the primordial spectrum. As discussed below, CMB data show that n = 1 is a very good approximation; in any case, very substantial tilts (n 0.8) are required to alter the conclusions significantly.