6.2. The peak-background split

We now consider the central mechanism of biased clustering, in which a rare high density fluctuation, corresponding to a massive object, collapses sooner if it lies in a region of large-scale overdensity. This `helping hand' from the long-wavelength modes means that overdense regions contain an enhanced abundance of massive objects with respect to the mean, so that these systems display enhanced clustering. The basic mechanism can be immediately understood via the diagram in figure 8; it was first clearly analysed by Kaiser (1984) in the context of rich clusters of galaxies. What Kaiser did not do was consider the degree of bias that applies to more typical objects; the generalization to consider objects of any mass was made by Cole & Kaiser (1989; see also Mo & White 1996 and Sheth et al. 2001).

Figure 8. The high-peak bias model. If we decompose a density field into a fluctuating component on galaxy scales, together with a long-wavelength `swell' (shown dashed), then those regions of density that lie above a threshold in density of times the rms will be strongly clustered. If proto-objects are presumed to form at the sites of these high peaks (shaded, and indicated by arrows), then this is a population with Lagrangian bias - i.e. a non-uniform spatial distribution even prior to dynamical evolution of the density field. The key question is the physical origin of the threshold; for massive objects such as clusters, the requirement of collapse by the present imposes a threshold of 2. For galaxies, there will be no bias without additional mechanisms to cause star formation to favour those objects that collapse first.

The key ingredient of this analysis is the mass function of dark-matter haloes. The universe fragments into virialized systems such that f (M) dM is the number density of haloes in the mass range dM; conservation of mass requires that M f (M) dM = ₀. A convenient related dimensionless quantity is therefore the multiplicity function, M²f (M) / ₀, which gives the fraction of the mass of the universe contained in haloes of a unit range in ln M. The simplest analyses of the mass function rest on the concept of a density threshold: collapse to a virialized object is deemed to have occurred where linear-theory averaged over a box containing mass M reaches some critical value _c. Generally, we shall assume the value _c = 1.686 appropriate for spherical collapse in an Einstein-de Sitter universe. Now imagine that this situation is perturbed, by adding some constant shift to the density perturbations over some large region. The effect of this is to perturb the threshold: fluctuations now only need to reach = _c - in order to achieve collapse. The number density is therefore modulated:

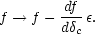(104)

This gives a bias in the number density of haloes in Lagrangian space: f / f = b_L , where the Lagrangian bias is

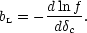(105)

In addition to this modulation of the halo properties, the large-scale disturbance will move haloes closer together where is large, giving a density contrast of 1 + . If << 1, the overall fractional density contrast of haloes is therefore the sum of the dynamical and statistical effects: _halo = + b_L . The overall bias in Eulerian space (b = _halo / ) is therefore

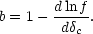(106)

Of course, the field can hardly be imposed by hand; instead, we make the peak-background split, in which is mentally decomposed into a small-scale and a large-scale component - which we identify with . The scale above which the large-scale component is defined does not matter so long as it lies between the sizes of collapsed systems and the scales at which we wish to measure correlations.

To apply this, we need an explicit expression for the mass function. The simplest alternative is the original expression of Press & Schechter (1974), which can be written in terms of the parameter = _c / (M):

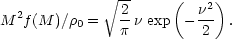(107)

We now use d / d_c = (M)^-1(d / d) = ( / _c)(d / d), since M is not affected by the threshold change, which yields

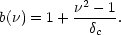(108)

This says that M^* haloes are unbiased, low-mass haloes are antibiased and high-mass haloes are positively biased, eventually reaching the b = / value expected for high peaks. The corresponding expression can readily be deduced for more accurate fitting formulae for the mass function, such as that of Sheth & Tormen (1999):

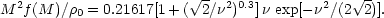(109)

We can now understand the observation that Abell clusters are much more strongly clustered than galaxies in general: regions of large-scale overdensity contain systematically more high-mass haloes than expected if the haloes traced the mass. This phenomenon was dubbed natural bias by White et al. (1987). However, applying the idea to galaxies is not straightforward: we have shown that enhanced clustering is only expected for massive fluctuations with 1, but galaxies at z = 0 fail this criterion. The high-peak idea applies will at high redshift, where massive galaxies are still assembling, but today there has been time for galaxy-scale haloes to collapse in all environments. The large bias that should exist at high redshifts is erased as the mass fluctuations grow: if the Lagrangian component to the biased density field is kept unaltered, then the present-day bias will tend to unity as

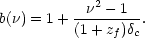(110)

(Fry 1986; Tegmark & Peebles 1998). Strong galaxy bias at z = 0 therefore requires some form of selection that locates present-day galaxies preferentially in the rarer haloes with M > M^* (Kauffmann, Nusser & Steinmetz 1997).

This dilemma forced the introduction of the idea of high-peak bias: bright galaxies form only at the sites of high peaks in the initial density field (Bardeen et al. 1986; Davis et al. 1985). This idea is commonly, but incorrectly, attributed to Kaiser (1984), but it needs an extra ingredient, namely a non-gravitational threshold. Attempts were therefore made to argue that the first generation of objects could propagate disruptive signals, causing neighbours in low-density regions to be `still-born'. It is then possible to construct models (e.g. Bower et al. 1993) in which the large-scale modulation of the galaxy density is entirely non-gravitational in nature. However, it turned out to be hard to make such mechanisms operate: the energetics and required scale of the phenomenon are very large (Rees 1985; Dekel & Rees 1987). These difficulties were only removed when the standard model became a low-density universe, in which the dynamical argument for high galaxy bias no longer applied.