7. ANISOTROPIES IN THE CMB

Despite the great progress in precise measurements of large-scale structure, we cannot achieve a complete specification of the cosmological model in this way alone. The vacuum energy is not probed, since this affects mainly the growth rate of structure - which is degenerate with bias evolution. The matter content is only constrained if we assume that n = 1, and even then we only measure _m if a value for h is supplied. A more complete picture is obtained if we include data on clustering at much earlier times: the anisotropy of the microwave background, which reaches us from z 1100. In addition to breaking degeneracies, studies of this sort also test the basic gravitational instability theory - which will be seen to work very well indeed over this redshift range. This section briefly reviews the physics of CMB anisotropies, and presents recent data. For more details, see e.g. Hu & Dodelson (2002), or Dodelson (2003).

7.1. Anisotropy mechanisms

Fluctuations in the 2D temperature perturbation field are treated similarly to density fluctuations, except that the field is expanded in spherical harmonics, so modes of different scales are labelled by multipole number, . Once again, we can define a `power per octave' measure for the temperature fluctuations:

(136)

where the C are another common way of representing the power. Note that 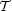²() is a power per ln; the modern trend is often to plot CMB fluctuations with a linear scale for - in which case one should really use 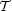²() / .

Figure 16. Illustrating the physical mechanisms that cause CMB anisotropies. The shaded arc on the right represents the last-scattering shell; an inhomogeneity on this shell affects the CMB through its potential, adiabatic and Doppler perturbations. Further perturbations are added along the line of sight by time-varying potentials (Rees-Sciama effect) and by electron scattering from hot gas (Sunyaev-Zeldovich effect). The density field at last scattering can be Fourier analysed into modes of wavevector k. These spatial perturbation modes have a contribution that is in general damped by averaging over the shell of last scattering. Short-wavelength modes are more heavily affected (i) because more of them fit inside the scattering shell, and (ii) because their wavevectors point more nearly radially for a given projected wavelength.

We now list the mechanisms that cause primary anisotropies in the CMB (as opposed to secondary anisotropies, which are generated by scattering along the line of sight). There are three basic primary effects, illustrated in figure 16, which are important on respectively large, intermediate and small angular scales:

(1) Gravitational (Sachs-Wolfe) perturbations. Photons from high-density regions at last scattering have to climb out of potential wells, and are thus redshifted:

(137)

(2) Intrinsic (adiabatic) perturbations. In high-density regions, the coupling of matter and radiation can compress the radiation also, giving a higher temperature:

(138)

(3) Velocity (Doppler) perturbations. The plasma has a non-zero velocity at recombination, which leads to Doppler shifts in frequency and hence brightness temperature:

(139)

To the above list should be added `tensor modes': anisotropies due to a background of primordial gravitational waves, potentially generated during an inflationary era (see below).

There are in addition effects generated along the line of sight. One important effect is the integrated Sachs-Wolfe effect, which arises when the potential perturbations evolve:

(140)

This happens both at early times (because radiation is still important) and late times (because of ). Other effects are to do with the development of nonlinear structure, and are mainly on small scales (principally the Sunyaev-Zeldovich effect from IGM Comptonization). The exception is the effect of reionization; to a good approximation, this merely damps the fluctuations on all scales:

(141)

where the optical depth must exceed 0.04, based on the highest-redshift quasars and the BBN baryon density. As we will see later, CMB polarization data have detected a signature consistent with = 0.17± 0.04, implying reionization at z 20.