2.5. Horizons

One of the most crucial concepts to master about FRW models is the existence of horizons. This concept will prove useful in a variety of places in these lectures, but most importantly in understanding the shortcomings of what we are terming the standard cosmology.

Suppose an emitter, e, sends a light signal to an observer, o, who is at r = 0. Setting = constant and = constant and working in conformal time, for such radial null rays we have _o - = r. In particular this means that

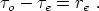(46)

Now suppose _e is bounded below by 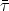_e; for example, 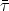_e might represent the Big Bang singularity. Then there exists a maximum distance to which the observer can see, known as the particle horizon distance, given by

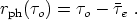(47)

The physical meaning of this is illustrated in figure 2.3.

Figure 2.3. Particle horizons arise when the past light cone of an observer o terminates at a finite conformal time. Then there will be worldlines of other particles which do not intersect the past of o, meaning that they were never in causal contact.

Similarly, suppose _o is bounded above by 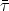_o. Then there exists a limit to spacetime events which can be influenced by the emitter. This limit is known as the event horizon distance, given by

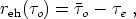(48)

with physical meaning illustrated in figure 2.4.

Figure 2.4. Event horizons arise when the future light cone of an observer o terminates at a finite conformal time. Then there will be worldlines of other particles which do not intersect the future of o, meaning that they cannot possibly influence each other.

These horizon distances may be converted to proper horizon distances at cosmic time t, for example

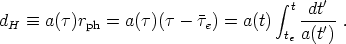(49)

Just as the Hubble time H₀^-1 provides a rough guide for the age of the universe, the Hubble distance cH₀^-1 provides a rough estimate of the horizon distance in a matter- or radiation-dominated universe.