2.6. Geometry, Destiny and Dark Energy

In subsequent lectures we will use what we have learned here to extrapolate back to some of the earliest times in the universe. We will discuss the thermodynamics of the early universe, and the resulting interdependency between particle physics and cosmology. However, before that, we would like to explore some implications for the future of the universe.

For a long time in cosmology, it was quite commonplace to refer to the three possible geometries consistent with homogeneity and isotropy as closed (k = 1), open (k = - 1) and flat (k = 0). There were two reasons for this. First, if one considered only the universal covering spaces, then a positively curved universe would be a 3-sphere, which has finite volume and hence is closed, while a negatively curved universe would be the hyperbolic 3-manifold 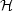³, which has infinite volume and hence is open.

Second, with dust and radiation as sources of energy density, universes with greater than the critical density would ultimately collapse, while those with less than the critical density would expand forever, with flat universes lying on the border between the two. for the case of pure dust-filled universes this is easily seen from (40) and (44).

As we have already mentioned, GR is a local theory, so the first of these points was never really valid. For example, there exist perfectly good compact hyperbolic manifolds, of finite volume, which are consistent with all our cosmological assumptions. However, the connection between geometry and destiny implied by the second point above was quite reasonable as long as dust and radiation were the only types of energy density relevant in the late universe.

In recent years it has become clear that the dominant component of energy density in the present universe is neither dust nor radiation, but rather is dark energy. This component is characterized by an equation of state parameter w < - 1/3. We will have a lot more to say about this component (including the observational evidence for it) in the next lecture, but for now we would just like to focus on the way in which it has completely separated our concepts of geometry and destiny.

For simplicity, let's focus on what happens if the only energy density in the universe is a cosmological constant, with w = - 1. In this case, the Friedmann equation may be solved for any value of the spatial curvature parameter k. If > 0 then the solutions are

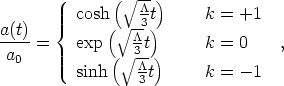(50)

where we have encountered the k = 0 case earlier. It is immediately clear that, in the t limit, all solutions expand exponentially, independently of the spatial curvature. In fact, these solutions are all exactly the same spacetime - de Sitter space - just in different coordinate systems. These features of de Sitter space will resurface crucially when we discuss inflation. However, the point here is that the universe clearly expands forever in these spacetimes, irrespective of the value of the spatial curvature. Note, however, that not all of the solutions in (50) actually cover all of de Sitter space; the k = 0 and k = - 1 solutions represent coordinate patches which only cover part of the manifold.

For completeness, let us complete the description of spaces with a cosmological constant by considering the case < 0. This spacetime is called Anti-de Sitter space (AdS) and it should be clear from the Friedmann equation that such a spacetime can only exist in a space with spatial curvature k = - 1. The corresponding solution for the scale factor is

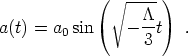(51)

Once again, this solution does not cover all of AdS; for a more complete discussion, see [20].