4.2. Particles in Equilibrium
The various particles inhabiting the early universe can be usefully characterized according to three criteria: in equilibrium vs. out of equilibrium (decoupled), bosonic vs. fermionic, and relativistic (velocities near c) vs. non-relativistic. In this section we consider species which are in equilibrium with the surrounding thermal bath.
Let us begin by discussing the conditions under which a particle
species will be in equilibrium with the surrounding thermal plasma.
A given species remains in thermal equilibrium as long as its
interaction rate is larger than the expansion rate of the
universe. Roughly speaking, equilibrium requires it to be possible for
the products of a given reaction have the opportunity to recombine in
the reverse reaction and if the expansion of the universe is rapid
enough this won't happen. A particle species for which the interaction
rates have fallen below the expansion rate of the universe is said to
have frozen out or decoupled. If the interaction rate of
some particle with the background plasma is
, it will
be decoupled whenever
 |
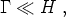(95) |
where the Hubble constant H sets the cosmological timescale.
As a good rule of thumb, the expansion rate in the early universe
is "slow," and particles tend to be in thermal equilibrium (unless
they are very weakly coupled). This
can be seen from the Friedmann equation when the energy density
is dominated by a plasma with
~
T4; we then have
 |
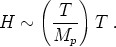(96) |
Thus, the Hubble parameter is suppressed with respect to the
temperature by a factor of T / Mp. At extremely
early times
(near the Planck era, for example), the universe may be expanding
so quickly that no species are in equilibrium; as the expansion
rate slows, equilibrium becomes possible. However, the interaction
rate for a particle
with cross-section 
is typically of the form
 |
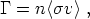(97) |
where n is the number density and v a typical particle
velocity. Since
n 
a-3, the density of particles will eventually
dip so low that equilibrium can once again no longer be maintained. In our
current universe, no species are in equilibrium with the background
plasma (represented by the CMB photons).
Now let us focus on particles in equilibrium. For a gas of weakly-interacting particles, we can describe the state in terms of a distribution function f (p), where the three-momentum p satisfies
 |
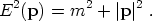(98) |
The distribution function characterizes the density of particles in a given momentum bin. (In general it will also be a function of the spatial position x, but we suppress that here.) The number density, energy density, and pressure of some species labeled i are given by
 |
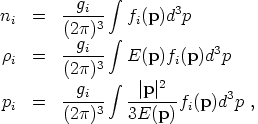(99) |
where gi is the number of spin states of the
particles. For massless photons we have
g
= 2, while for a massive vector
boson such as the Z we have gZ = 3. In
the usual accounting, particles and antiparticles are treated as
separate species; thus, for spin-1/2 electrons and positrons we have
ge- = ge+ =
2. In thermal equilibrium at a temperature
T the particles will be in either
Fermi-Dirac or Bose-Einstein distributions,
 |
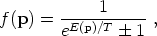(100) |
where the plus sign is for fermions and the minus sign for bosons.
We can do the integrals over the distribution functions in
two opposite limits: particles which are highly relativistic
(T >> m) or highly non-relativistic (T
<< m).
The results are shown in table 2, in which
is the Riemann zeta function, and
(3)
1.202.
 |
From this table we can extract several pieces of relevant information. Relativistic particles, whether bosons or fermions, remain in approximately equal abundances in equilibrium. Once they become non-relativistic, however, their abundance plummets, and becomes exponentially suppressed with respect to the relativistic species. This is simply because it becomes progressively harder for massive particle-antiparticle pairs to be produced in a plasma with T << m.
It is interesting to note that, although matter is much more dominant than radiation in the universe today, since their energy densities scale differently the early universe was radiation-dominated. We can write the ratio of the density parameters in matter and radiation as
 |
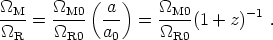(101) |
The redshift of matter-radiation equality is thus
 |
(102) |
This expression assumes that the particles that are non-relativistic today were also non-relativistic at zeq; this should be a safe assumption, with the possible exception of massive neutrinos, which make a minority contribution to the total density.
As we mentioned in our discussion of the CMB in the previous lecture, even decoupled photons maintain a thermal distribution; this is not because they are in equilibrium, but simply because the distribution function redshifts into a similar distribution with a lower temperature proportional to 1 / a. We can therefore speak of the "effective temperature" of a relativistic species that freezes out at a temperature Tf and scale factor af:
 |
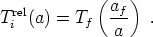(103) |
For example, neutrinos decouple at a temperature around 1 MeV; shortly thereafter, electrons and positrons annihilate into photons, dumping energy (and entropy) into the plasma but leaving the neutrinos unaffected. Consequently, we expect a neutrino background in the current universe with a temperature of approximately 2K, while the photon temperature is 3K.
A similar effect occurs for particles which are non-relativistic at decoupling, with one important difference. For non-relativistic particles the temperature is proportional to the kinetic energy 1/2 mv2, which redshifts as 1/a2. We therefore have
 |
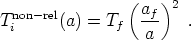(104) |
In either case we are imagining that the species freezes out while relativistic/non-relativistic and stays that way afterward; if it freezes out while relativistic and subsequently becomes non-relativistic, the distribution function will be distorted away from a thermal spectrum.
The notion of an effective temperature allows us to define a corresponding notion of an effective number of relativistic degrees of freedom, which in turn permits a compact expression for the total relativistic energy density. The effective number of relativistic degrees of freedom (as far as energy is concerned) can be defined as
 |
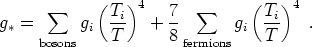(105) |
(The temperature T is the actual temperature of the background plasma, assumed to be in equilibrium.) Then the total energy density in all relativistic species comes from adding the contributions of each species, to obtain the simple formula
 |
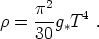(106) |
We can do the same thing for the entropy density. From (94), the entropy density in relativistic particles goes as T3 rather than T4, so we define the effective number of relativistic degrees of freedom for entropy as
 |
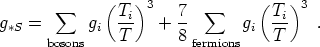(107) |
The entropy density in relativistic species is then
 |
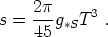(108) |
Numerically, g* and g*S will typically be very close to each other. In the Standard Model, we have
 |
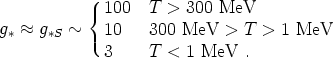(109) |
The events that change the effective number of relativistic degrees of freedom are the QCD phase transition at 300 MeV, and the annihilation of electron/positron pairs at 1 MeV.
Because of the release of energy into the background plasma when
species annihilate, it is only an approximation to say that the
temperature goes as
T 1 /
a. A better approximation is to
say that the comoving entropy density is conserved,
 |
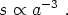(110) |
This will hold under all forms of adiabatic evolution; entropy will only be produced at a process like a first-order phase transition or an out-of-equilibrium decay. (In fact, we expect that the entropy production from such processes is very small compared to the total entropy, and adiabatic evolution is an excellent approximation for almost the entire early universe. One exception is inflation, discussed in the next lecture.) Combining entropy conservation with the expression (108) for the entropy density in relativistic species, we obtain a better expression for the evolution of the temperature,
 |
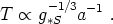(111) |
The temperature will consistently decrease under adiabatic evolution in an expanding universe, but it decreases more slowly when the effective number of relativistic degrees of freedom is diminished.