4.4. Vacuum displacement

Another important possibility is the existence of relics which were never in thermal equilibrium. An example of these will be discussed later in this lecture: the production of topological defects at phase transitions. Let's discuss another kind of non-thermal relic, which derives from what we might call "vacuum displacement." Consider the action for a real scalar field in curved spacetime:

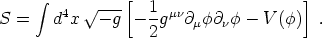(121)

If we assume that is spatially homogeneous (_i = 0), its equation of motion in the Robertson-Walker metric (5) will be

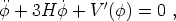(122)

where an overdot indicates a partial derivative with respect to time, and a prime indicates a derivative with respect to . For a free massive scalar field, V() = 1/2 m^{2 2}, and (122) describes a harmonic oscillator with a time-dependent damping term. For H > m the field will be overdamped, and stay essentially constant at whatever point in the potential it finds itself. So let us imagine that at some time in the very early universe (when H was large) we had such an overdamped homogeneous scalar field, stuck at a value = _*; the total energy density in the field is simply the potential energy 1/2 m² _*². The Hubble parameter H will decrease to approximately m when the temperature reaches T_* = (m M_p)², after which the field will be able to evolve and will begin to oscillate in its potential. The vacuum energy is converted to a combination of vacuum and kinetic energy which will redshift like matter, as a^-3; in a particle interpretation, the field is a Bose condensate of zero-momentum particles. We will therefore have

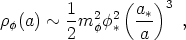(123)

which leads to a density parameter today

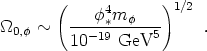(124)

A classic example of a non-thermal relic produced by vacuum displacement is the QCD axion, which has a typical primordial value <> ~ f_PQ and a mass m ~ _QCD / f_PQ, where f_PQ is the Peccei-Quinn symmetry-breaking scale and _QCD ~ 0.3 GeV is the QCD scale [1]. In this case, plugging in numbers reveals

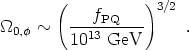(125)

The Peccei-Quinn scale is essentially a free parameter from a theoretical point of view, but experiments and astrophysical constraints have ruled out most values except for a small window around f_PQ ~ 10¹² GeV. The axion therefore remains a viable dark matter candidate [115, 116]. Note that, even though dark matter axions are very light (_QCD² / f_PQ ~ 10^-4 eV), they are extremely non-relativistic, which can be traced to the non-thermal nature of their production process. (Another important way to produce axions is through the decay of axion cosmic strings [1, 117].)