5.5. Slowly-Rolling Scalar Fields

If inflation is to solve the problems of the standard cosmology, then it must be active at extremely early times. Thus, we would like to address the earliest times in the universe amenable to a classical description. We expect this to be at or around the Planck time t_P and since Planckian quantities arise often in inflation we will retain values of the Planck mass in the equations of this section. There are many models of inflation, but because of time constraints we will concentrate almost exclusively on the chaotic inflation model of Linde. We have borrowed heavily in places here from the excellent text of Liddle and Lyth [7].

Consider modeling matter in the early universe by a real scalar field , with potential V(). The energy-momentum tensor for is

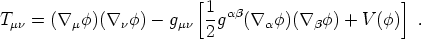(188)

For simplicity we will specialize to the homogeneous case, in which all quantities depend only on cosmological time t and set k = 0. A homogeneous real scalar field behaves as a perfect fluid with

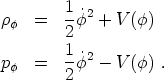(189) (190)

The equation of motion for the scalar field is given by

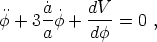(191)

which can be thought of as the usual equation of motion for a scalar field in Minkowski space, but with a friction term due to the expansion of the universe. The Friedmann equation with such a field as the sole energy source is

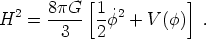(192)

A very specific way in which accelerated expansion can occur is if the universe is dominated by an energy component that approximates a cosmological constant. In that case the associated expansion rate will be exponential, as we have already seen. Scalar fields can accomplish this in an interesting way. From (189) it is clear that if ² << V() then the potential energy of the scalar field is the dominant contribution to both the energy density and the pressure, and the resulting equation of state is p - , approximately that of a cosmological constant. the resulting expansion is certainly accelerating. In a loose sense, this negligible kinetic energy is equivalent to the fields slowly rolling down its potential; an approximation which we will now make more formal.

Technically, the slow-roll approximation for inflation involves neglecting the 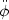term in (191) and neglecting the kinetic energy of compared to the potential energy. The scalar field equation of motion and the Friedmann equation then become

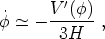(193)

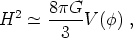(194)

where in this lecture a prime denotes a derivative with respect to .

These conditions will hold if the two slow-roll conditions are satisfied. These are

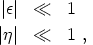(195)

where the slow-roll parameters are given by

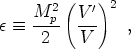(196)

and

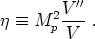(197)

It is easy to see that the slow roll conditions yield inflation. Recall that inflation is defined by / a > 0. We can write

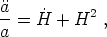(198)

so that inflation occurs if

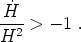(199)

But in slow-roll

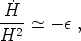(200)

which will be small. Smallness of the other parameter helps to ensure that inflation will continue for a sufficient period.

It is useful to have a general expression to describe how much inflation occurs, once it has begun. This is typically quantified by the number of e-folds, defined by

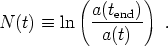(201)

Usually we are interested in how many efolds occur between a given field value and the field value at the end of inflation _end, defined by (_end) = 1. We also would like to express N in terms of the potential. Fortunately this is simple to do via

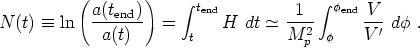(202)

The issue of initial conditions for inflation is one that is quite subtle and we will not get into a discussion of that here. Instead we will remain focused on chaotic inflation, in which we assume that the early universe emerges from the Planck epoch with the scalar field taking different values in different parts of the universe, with typically Planckian energies. There will then be some probability for inflation to begin in some places, and we shall focus on those.