5.6. Attractor Solutions in Inflation

For simplicity, let us consider a particularly simple potential

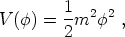(203)

where m has dimensions of mass. We shall also assume initial conditions that at the end of the quantum epoch, which we label as t = 0, ~ M_p⁴.

The slow-roll conditions give that, at t = 0,

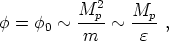(204)

where we have defined m / M_p << 1. We also have

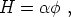(205)

where

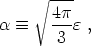(206)

so that the scalar field equation of motion becomes

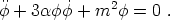(207)

This is solved by

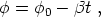(208)

where m² / 3. Now, the slow-roll conditions remain satisfied provided that

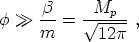(209)

and therefore, (208) is valid for a time

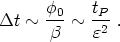(210)

Why is this important? This is important because (208) is an attractor solution! Let's see how this arises. Consider perturbing (208) by writing

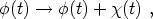(211)

where (t) is a "small" perturbation, substituting in to the equation of motion and linearizing in . One obtains

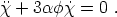(212)

This equation exhibits two solutions. The first is just a constant, which just serves to move along the trajectory. The second solution is a decaying mode with time constant t_c = (3 )^-1. Since t_c << t, all solutions rapidly decay to (208) - it is an attractor.