15.2. BASIC RELATIONS

The flux density S as a function of frequency and the angular size of a radio source are the observables directly relevant to most cosmological problems. They are related to the intrinsic source luminosity L and projected linear size d as described below.

Consider an isotropic source at redshift z with spectral luminosity L at frequency (measured in the source frame). Its spectral flux density S measured at the same frequency (in the observer's frame) will be

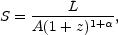(15.1)

where A is the area of the sphere centered on the source and containing the observer and - ln(S / S₀) / ln( / ₀) is the two-point spectral index between the frequencies and ₀ = / (1 + z) in the observer's frame. (Note that the negative sign convention for is used throughout this chapter.) The (1 + z)¹⁺ term expresses the special relativistic Doppler correction; the geometry and expansion dynamics of the universe appear only in A. An "effective distance" D (Longair 1978) can be defined by A 4 D². Since the area of the sphere centered on the observer and containing a source at redshift z is always A / (1 + z)², the relation between (projected) linear size d and measured angular size is

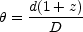(15.2)

The "angular size" distance is defined by D d / = D / (1 + z). The "bolometric luminosity distance" D_bol defined by S_bol = L_bol / (4 D_bol²) is given by D_bol = D(1 + z).

In Friedmann models (cosmological constant = 0) with zero pressure, density parameter = 2q₀, and current Hubble parameter H₀ the effective distance is traditionally given (Mattig 1958) as

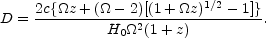(15.3)

However, this formula is numerically unstable for small z, the transformation (based on Terrell 1977)

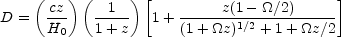(15.4)

is better for numerical calculations. For particular values of , D reduces to the simpler forms:

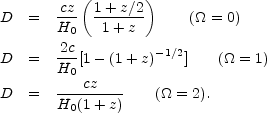(15.5a) (15.5b) (15.5c)

To describe the distributions of sources in space and time, we also need the comoving volume dV of the spherical shell extending from z to z + dz. It is dV = 4 D² dr, where the comoving radial coordinate element is dr = - (1 + z)c dt. In a Friedmann universe the expansion rate is

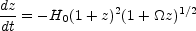(15.6)

so

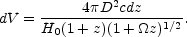(15.7)