3.4. Magnetic fields derived from IC emission

When the synchrotron radio and IC X-ray emission are produced by the same population of relativistic electrons (see Secs. 3.1 and 3.3), the total synchrotron and IC powers are related. The IC emissivity is proportional to the energy density in the photon field, u_ph, which for the cosmological blackbody radiation is ~ 5 × 10^-13 (1 + z)⁴ erg cm^-3, whereas the synchrotron emissivity is proportional to the energy density in the magnetic field, u_B = B² / 8. This leads to a simple proportionality between synchrotron and IC luminosities:

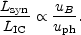(29)

Combining the standard formulae of the synchrotron and Compton emission mechanisms, the radio and HXR detections directly yield some of the basic properties of the magnetic field. Following Blumenthal and Gould [13], the synchrotron flux at the radio frequency _r and the IC X-ray flux at frequency _x are (all parameters in cgs units):

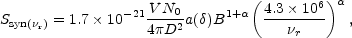(30)

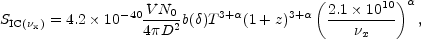(31)

where the functions a() and b() are tabulated in Table 2, V is the emission volume, and D the source distance. From the ratio between the X-ray and radio fluxes, one derives an estimate of the total magnetic field, averaged over the emitting volume.

Table 2. Inverse Compton parametrization

		a()	b()	h()
0.0	1	0.283	3.20	1.32 × 10-16
0.1	1.2	0.209	3.42	2.13 × 10-16
0.2	1.4	0.164	3.73	3.31 × 10-16
0.3	1.6	0.136	4.12	5.06 × 10-16
0.4	1.8	0.117	4.62	7.71 × 10-16
0.5	2.0	0.103	5.25	1.19 × 10-15
0.6	2.2	0.093	6.03	1.89 × 10-15
0.7	2.4	0.086	7.00	3.17 × 10-15
0.8	2.6	0.081	8.20	5.95 × 10-15
0.9	2.8	0.077	9.69	1.48 × 10-14
1.0	3.0	0.074	11.54	see Eq. 34
1.1	3.2	0.072	13.85	-2.24 × 10-14
1.2	3.4	0.071	16.74	-1.37 × 10-14
1.3	3.6	0.071	20.35	-1.12 × 10-14
1.4	3.8	0.072	24.89	-1.02 × 10-14
1.5	4.0	0.073	30.62	-9.88 × 10-15
1.6	4.2	0.075	37.87	-9.96 × 10-15
1.7	4.4	0.076	47.07	-1.03 × 10-14
1.8	4.6	0.079	58.78	-1.09 × 10-14
1.9	4.8	0.083	73.74	-1.16 × 10-14
2.0	5.0	0.087	92.90	-1.25 × 10-14

To obtain a formula for practical use, we first relate the monochromatic X-ray flux S_IC(x) to the flux S_IC(E1-E2) integrated over the energy interval E₁ - E₂, as this is the parameter usually measured from observations:

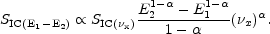(32)

We also substitute the radiation temperature T = 2.7 K at z = 0, and we compute the constants for commonly used units. We obtain the magnetic field as:

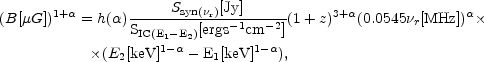(33)

where the function h() is tabulated in Table 2. For = 1, the above formula becomes

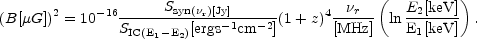(34)

The difficulties related to this method are essentially due to the limitations of present X-ray observations in the hard X-ray domain and to the problem of distinguishing between the non-thermal and the thermal X-ray emission. When the IC X-ray emission is not detected from a radio emitting region, only lower limits to the magnetic fields can be derived.