12.5.6. Inverse Compton Scattering

The maximum brightness temperature of any opaque synchrotron source is limited by inverse Compton scattering to about 10¹² ° K. This is the brightness temperature corresponding to the case where the energy loss by synchrotron radiation is equal to the energy loss by inverse Compton scattering and may be derived as follows (Kellermann and Pauliny-Toth, 1969).

For a homogeneous isotropic source

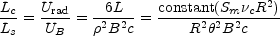(12.23)

where L_c = power radiated by inverse Compton scattering, L_s = radio power radiated by synchrotron emission, 4 r² _m^c S d ~ 4 r² S_{m c}, U_rad = 3L / 4 r² c = energy density of the radiation field, U_B = B² / 8 = energy density of the magnetic field, R = the distance to the source, = angular size, and the radius = R / 2. Then using Equation (12.22) and recognizing that S_m / ^{2 2} is proportional to the peak brightness temperature, T_m, and including the effect of second-order scattering, we have

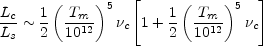(12.24)

where _c is the upper cut-off frequency in MHz. Taking _c ~ 100 GHz, then for T_m < 10¹¹ °K, L_c / L_s << 1 and inverse Compton scattering is not important; but for T_m > 10¹² °K, the second-order term becomes important, L_c / L_s ~ (T_m / 10¹²)¹⁰, and the inverse Compton losses become catastrophic. The exact value of T_m corresponding to L_c / L_s = 1 is somewhat dependent on the specific geometry, the value of , and the spectral cut-off frequency _c, but the strong dependence of L_c / L_s on T_m implies that T_m cannot significantly exceed 10¹² °K, independent of wavelength. This places a lower limit to the angular size of

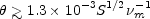(12.25)

If the compact sources expand with conservation of magnetic flux, then T_m varies with radius as T_m ^{-(-1) / (+4)}, so that for ~ 1, T_m remains constant and otherwise depends only weakly on .