12.5.5. Synchrotron Self-Absorption

In Sections 12.5.2 and 12.5.3 we have assumed that the flux from a group of relativistic electrons is merely the arithmetical sum of the radiation from the individual electrons, i.e., the electron gas is assumed to be transparent. If, however, the apparent brightness temperature of the source approaches the equivalent kinetic temperature of the electrons, then self-absorption will become important and part of the radiation is absorbed. The precise form of the radiation spectrum is complex, but can be calculated from the emission and absorption coefficients of relativistic electrons in a magnetic field. The parameters depend on the electron energy and pitch-angle distributions and can be determined only from numerical integrations. The form of the spectrum in the limiting case of a completely opaque source may be derived quite straightforwardly, however. Consider the radiation from an optically thick blackbody of solid angle at temperature T. The observed flux density is

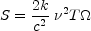(12.20)

If the optically thick relativistic electron gas is described as a blackbody whose temperature is given by the equivalent kinetic temperature of the electrons, E = kT, then using Equation (12.16), we can write

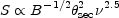(12.21)

In other words, the source may be thought of as a blackbody (S ²) whose temperature (energy) depends on the square root of the frequency (E _c^1/2).

Rewriting Equation (12.21) and using a more precise analysis, including the small dependence on the index and the effect of the redshift z, the magnetic field is given by

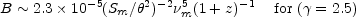(12.22)

where S_m is the maximum flux density at the self-absorption cut-off frequency, _m is in GHz, and is in milliarc seconds.

Although the apparent effect of synchrotron self-absorption is evident in many sources where indices as steep as +1 are often observed at long wavelengths, there has not been any direct observation of the theoretically expected value of +2.5. This has led some to question whether or not the observed low-frequency cut-offs are in fact due to self-absorption. However, this argument is probably irrelevant for the same reason that the theoretical index of +2.0 is never observed in the thermal emission spectra of the familiar HII regions. The explanation in both cases is that there is a wide range of opacities in these sources which cause different parts of the source to become opaque at different wavelengths, producing a gradual, rather than a sharp, transition from the transparent to the opaque case.