If you believe that a spiral arm exists over a very large dis-
tance in the Galaxy, you would probably also like to believe
that it exists over many rotation periods.
Prendergast 1967,
p.304
In the beginning the immediate necessity was a consistent de-
scription of the spiral phenomenon, in sufficiently good agree-
ment with the observational data.
Bertin 1980, p.10
The Lin-Shu Milky-Way spiral diagram favorably met at the Noordwijk 1966 IAU Symposium (Lin & Shu 1967), its authors affirmed that their wave theory already "produced conclusions which appear satisfactory from a general point of view". It was declared "free from the kinematical difficulty of differential rotation" 28 and permitting "the existence of a [two-armed trailing] spiral pattern over the whole disk while allowing the individual spiral arms to be broken and fragmentary" (Lin 1967b, pp.459, 462; Lin 1968, p.47). This optimism gave Lin a feeling of confidence, correctness and leadership in the understanding of galactic spiral phenomenon, feeding his further initiative.
2.1. Neutral modes and marginally stable disk
... a number of major improvements and further extensions
of the theory.
Shu 1968, p.5
Still, a posteriori, the behavior of the system is remarkably
simple, and the use of asymptotics is a generous source of
physical insight.
Bertin & Lin
1996, p.219
To Shu, his historic early coauthor, Lin posed the important task of enriching the analytical attire of their `theory of density waves', and Shu supplied some in his PhD thesis work "The Dynamics and Large-Scale Structure of Spiral Galaxies", presented at Harvard in early 1968 (Shu 1968, hereinafter S68). 29 He started with the derivation of a general integral equation for self-consistent responses in a thin star disk. Kalnajs (1965) already had one in an epicyclic approximation, attacking it for growing-mode solutions, but uninspired by those arduous efforts, Shu was not in the mood to vie with him in direct modal search, the more so as, following Lin, he targeted only tightly wrapped neutral modes. This converted his practical interest in the integral equation to analyzing its short-wavelength limit in the 2nd WKBJ order. For the day, it was a rather worthy plan as for instance it seemed to allow access to the radial behavior of the supposedly long-lived modes.
"We start with the hypothesis that a neutral spiral density wave exists. We then investigate the question whether such waves can be self-sustained in the presence of differential rotation and finite velocity dispersion. In this way, we are able to study, in a qualitative manner, the characteristics of such self-sustained waves. This deals with the question of persistence. [...] We investigate the question how such waves can be expected to attain finite amplitudes, and what mechanism is that allows them to take on a spiral rather than a barred form. This deals with the question of origin" (S68, p.6)
In his attempts of answering the so posed `question of persistence', Shu resourcefully argued for adoption of the marginally stable galaxy-disk model, and turning then to the `question of origin', he called for the idea of overstability with which to resolve the `antispiral theorem' in favor of a trailing quasi-stationary spiral mode.
Lin and Shu initially ascribed a quasi-stationary spiral structure to an in-places-strongly-unstable star disk (Lin & Shu 1964), but soon they changed their mind (Lin and Shu 1966) for Toomre's early idea of the disk entirely evolving to a state of marginal stability Q = 1 (Toomre 1964a). Toomre himself had already left it, having considered the role gas clouds must have on stars, which Julian's calculations soon supported (Julian 1967), however Lin and Shu remained skeptical of any need for Q to rise above unity.
Lin: "Toomre (1964a) gave a criterion for the minimum dispersion velocity needed to prevent gravitational collapse. He and Julian (JT) are inclined to believe, however, that the mean square dispersion velocity might exceed this minimum by as large a factor as 1.8. On the other hand, Lin and Shu (1966) are inclined to believe that the value would not significantly exceed the minimum needed [...] Since observations show deviations from a Schwarzschild distribution, it is difficult to distinguish between these two opinions without a careful analysis of the observational data." (Lin 1968, p.49)
Shu: "Whether the Galaxy is everywhere more than marginally stable is a point of some debate. Julian (1967) is of the opinion that the enhancement of cooperative effects of the irregular forces provided by massive objects (on the order of 106 - 107 solar masses each) will inevitably drive Q to values substantially higher than unity. Observations in the plane of the Galaxy show only the `spiral arms' to possess large mass concentrations." (Shu 1970c, p.111) "In the density-wave theory of spiral structure (Lin and Shu 1964, 1966), large aggregations of interstellar gas are the manifestation of a density wave and do not represent either a bound or a quasi-permanent body of matter. The interaction of stars with such a wave does not lead to appreciable relaxation." (Shu 1969, p.506)
This troublesome climate prompted Lin and Shu to reverse the logic of
thinking and they put, accordingly, that their pioneer Noordwijk plot best
attested its underlying Q = 1 star disk. Shu examined Lynden-Bell's
mechanism of violent relaxation and claimed it not occurring in disk
conditions. "The only relaxation mechanism operative for stars in the early
life of such galaxies, he thus argued, is an axisymmetric form of the Jeans
instability discussed by Toomre"
(Shu 1969, p.505);
it develops in the disk
plane and affects neither vertical distribution of stars nor their angular
momentum. Along the event sequence Shu proposed for this mechanism, our
young, still gaseous Galaxy first attains a disk form. Via shear
deformation, its mass distribution becomes axisymmetric, and turbulent gas
motions get fixed at a permanent level c comparable to today's
vertical
stellar velocity dispersion. There comes a period of violent star formation.
The baby stars, inheriting parental kinematics, gain an isotropic rms
velocity c. The fresh cold disk they arrange is a fit subject for the
operation of axisymmetric instability through which it heats up until a
stage Q 
1 is
reached. The process cannot go beyond it, and losing the heat is also
impossible owing to the lack of any plausible cooling of the stars
(Shu 1968,
1969,
1970c).
In the adoption of
Q 1 Lin and Shu
found two attractive factors. One was that in this neutral-mode case the
four dispersion-curve branches seemed to converge at corotation
= 0
(Fig.5). Shu conceived that two
longer-wave branches, due mainly to differential rotation, are "more in the
nature of pulsations", and two other, determined primarily by velocity
dispersion, are "more in the nature of local oscillations" (S68,
p.108). Still,
well seeing that these two processes are present in varying degrees here and
there in the disk, he found this "useful for conceptual purposes" insight
"somewhat arbitrary" and credited realistic `coherent' spirals "without a
`kink' at = 0" to a proposed
`Mode-A' meant to couple the short-wave
branch inside corotation with its long-wave counterpart outside the
same. 30 This smooth and
conscious selection, Shu noticed, had already served him and Lin in 1966
with their Noordwijk Milky-Way spiral understood as the inner half of
Mode-A.
 |
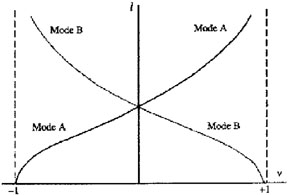Figure 5. Shu's Mode-A as proposed by him to account for the grand design in non-barred spiral galaxies. (The figure combines two separate figures from Shu 1968) |
Lin and Shu hoped that "after a galaxy has been completely stabilized against Jeans' condensational instability, it is still susceptible to a mild overstability of two-armed waves" to which one owes actual spiral formation (S68, p.8). 31 Shu developed this theme in his thesis. In 1967 he learned from Toomre about his tentative group-velocity results and misused those to visualize how the individual wave crests move radially. He did not think then of genuine spiral-wave packets (see Sect. 3.2) and what he had was but a group of tightly wrapped two-armed waves somehow occurring to a galaxy and soon developing into an almost self-sustained mode, to get perfectly so via slight shearing and other modifications when it would gain and fix its amplitude. But if such a wave-crest group is not quite a mode yet, why not to apply to it group-velocity formulas? Shu did so and there he saw "another (and perhaps more important)" attraction due to the Q = 1 model (S68, p.111): his near-Mode-A got an inward radial group motion that "does not reverse sign somewhere in the principal range" between the inner and outer Lindblad resonances (ILR and OLR hereinafter). 32 In the inhomogeneous overstable disk such a motion "would lead to the growth of a `group' of spiral waves to some finite amplitude, the growth being ultimately limited by non-linear effects [...of] the shearing effects of differential rotation (which is absent in the linear theory) [that] may be expected to enhance any preference for trailing patterns." (p.8) 33
These overstability ideas Shu directly associated with the antispiral theorem that "a number of us have sometimes been worried" about (Prendergast 1967, p.308).
28 Woltjer, the key player who turned Lin to galaxy dynamics, stated in his spiral review that the density-wave theory as pictured by Lindblad already "resolves the kinematical difficulties, but of course a dynamic justification is needed" (Woltjer 1965, p.570). Lin (1967b, p.458) soon claimed that his and Shu's theory resolves the same as well. Back.
29 "Much of the credit for this investigation belongs to Professor C.C. Lin who asked the key question concerning the spiral structure of disk galaxies and then formulated the basic approach toward the resolution of the problem. [...] Professor M. Krook provided much generous help in his capacity as my faculty advisor and official thesis supervisor. Without his guidance and patience, my progress as a graduate student at Harvard would not have been as pleasant. Discussions with Dr. A. Kalnajs have cast light on several major and subtle points. Many of the more fruitful approaches were found only because of his well-raised criticisms of the form of the theory prevailing at one time. I have made use of some ideas of Professors A. Toomre and P. Vandervoort and am indebted to them on that account. Professor Toomre's helpful criticisms of various aspects of this research invariably proved to be illuminating. [...] The arrangement and style [of the final draft of the manuscript] were greatly improved by several suggestions made by Professor C.C. Lin. To all of these people, I am extremely grateful". (S68, p.i) Back.
30 Shu's proposed `Mode-B' combined the long waves inside and short waves outside corotation. "Formally, Mode-B spirals with m = 2 would present the appearance of a barred spiral" (S68, p.123). Back.
31 Overstability meant to Lin and Shu (Lin & Shu 1966; Lin 1967a) slow growth of waves traveling in an inhomogeneous Q = 1 disk. Back.
32 It is this mode, Lin and Shu believed, that manifests itself in the observed spiral structure, and only by superposing the identical `near-mode' with opposite sense of winding and direction of motion that "we obtain pure standing waves which do not propagate. Such a wave, of course, does not have any spiral features." (S68, p.113) Back.
33 Lin and Shu knew well that the shear, which was absent in their wave-mode theory, was absolutely present in the alternative, sheared-wave theory (GLB, JT) and that it there supported nothing but trailing waves. At the time they (and not only they) thought, however, that there was no intrinsic connection between these two types of density-wave theories. From their own end, they were not very successful in the 1960s in explaining the trailing-spiral prevalence, though that had been a vital test for any spiral theory. As regards their repeated mentions of and hints at nonlinear effects (Lin & Shu 1966; Lin 1967b, 1968), Lin and Shu never went into it very seriously. Besides, their view of mild instability favored trailing waves only inside corotation, diagnosing that "there might be a preference of leading waves in the [Galaxy's] range 10-12 kpc". Lin (1967a, p.80-81) professed that this "cannot be taken on face value", and largely to avoid the trouble he left his original grand spiral plan over the entire `principal region' between the m = 2 ILR and OLR for a conceptually different but yet space-preserving variant with corotation just transplanted to safer areas of disk outskirts or thereabouts.
Soon Contopoulos (1970a, b) calculated near-ILR stellar orbits subjected to a growing imposed Lin-Shu spiral gravity field of leading and trailing planforms. He got trailing responses in both cases and explained his result in terms of a specific character of misalignment of solutions inside and outside ILR, considering this the first strict demonstration of the Lin-Shu-wave trailing. Back.