Annu. Rev. Astron. Astrophys. 2003. 41: 191-239 Copyright © 2003 by Annual Reviews. All rights reserved

6. SIMPLE COOLING FLOW MODELS

To illustrate the influence and relevance of various terms in Equations (3) - (5), we briefly describe several simple time-dependent solutions (also see Loewenstein & Mathews 1987). For a reference flow we consider an E0 galaxy with no conductive or AGN heating and no source of gas except that lost from the stars, i.e. an "isolated" elliptical galaxy. The calculations begin at cosmic time t_in = 1 Gyr when we imagine that the (recently assembled) galaxy has just been cleared of gas by Type II supernovae. We assume NGC 4472 parameters with an NFW group halo of mass M_h = 4 × 10¹³ M and supernova rate SNu(t) = SNu(t_n)(t / t_n)^-s with SNu(t_n) = 0.06 and s = 1. In this reference model gas cools only at the galactic center and for simplicity we ignore the (not insignificant) gravitational influence of the cooled gas on hot gas near the origin; with this assumption the solutions are less sensitive to t_in. After the flow evolves to time t_n = 13 Gyrs we compare the density and temperature profiles with those of NGC 4472 and consider the mass that has cooled and the iron abundance in the hot gas. The stellar iron abundance is z_{*, Fe} = 0.75[1 + (r / R_e)²]^-0.2 (in solar meteoritic units) and 0.7 M of iron is contributed by each Type Ia supernova. Then we describe the effect on the reference solution when one of the many terms and parameters in Equations (3) - (5) is altered. None of these models agrees completely with the observations although some agree much better than others.

Reference Flow: The reference model at time t_n, shown with solid lines in column 1 of Figure 5, clearly has a steeper density slope than the observed profile and the temperature beyond about 5 kpc is too low. Both of these discrepancies occur in large part because our reference model galaxy is "isolated". The real NGC 4472 galaxy is (or was) surrounded by an extended circumgalactic cloud of gas at the somewhat higher virial temperature of the dark matter potential of the galaxy group from which NGC 4472 formed. As we discussed earlier, the excess gas density inside r ~ 10 kpc is a characteristic feature of all flow models except those with additional non-thermal pressure or heating. The temperature gradient dT/dr is negative in disagreement with observations of NGC 4472 and other similar galaxies (Figure 2b). Negative dT / dr occurs because of the steepness of the stellar potential in r R_e. When the reference calculation is repeated ignoring the stellar gravity but retaining only the softer NFW potential, T(r) passes through a maximum around r ~ 40 kpc and dT / dr > 0 within this radius, similar to cooling flow thermal profiles in rich clusters. For the reference flow we find L_{x, bol}(t_n) = 6.7 × 10⁴¹ ergs s^-1 from the hot diffuse gas. The iron abundance in the hot gas at r ~ 10 kpc, z_Fe / z_Fe, ~ 2.7 (meteoritic), is slightly higher than observed in the hot gas of NGC 4472, z_Fe / z_Fe, ~ 2 (e.g. Buote et al. 2000a, 2000c), even though our reference SNu(t_n) = 0.06 is rather low.

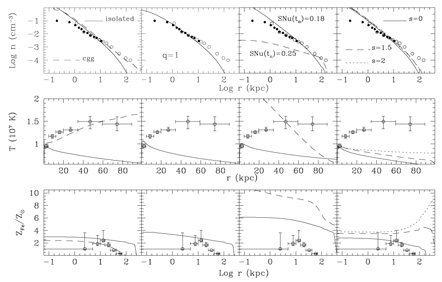Figure 5. A variety of computed time dependent galactic flow models are compared at time tn = 13 Gyrs with the observed gas density (top row) and temperature (middle row) of NGC 4472 taken from Figure 2. The bottom row shows the computed hot gas iron abundance compared with the observations of Buote (2000c). First column: A plot of the profiles at tn for an approximate model of NGC 4472 assuming an isolated galaxy (solid lines); this "reference" flow is based on an assumed parameter set as explained in the text. A similar galactic flow but including initial circumgalactic gas ("cgg") is also shown (dashed lines). Second column: A model similar to the reference flow but with ad hoc spatially distributed cooling with dropout parameter q = 1. Third column: Two flows similar to the reference flow (for which SNu(tn) = 0.06) but with additional heating by Type Ia supernovae: SNu(tn) = 0.18 (solid lines) and SNu(tn) = 0.25 (dashed lines). Fourth column: Three galactic flows similar to the reference flow but calculated with different past Type Ia supernova rates SNu(t) t-s: s = 0 (solid lines), 1.5 (dashed lines) and 2 (dotted lines). In the reference model s = 1.3.

Circumgalactic Gas: The dashed lines in column 1 of Figure 5 show the effect of including circumgalactic, group-related gas in the NGC 4472 evolution (Thomas 1986; Bertin & Toniazzo 1995; Brighenti & Mathews 1998). Agreement with the observations is improved in several ways: (1) By design the gas density beyond the optical galaxy (r 10 kpc) is increased to fit the data. (2) Since the virial temperature of the NFW group halo exceeds that of the central galaxy, the gas temperature of the circumgalactic gas is higher. As hot circumgalactic gas flows inward, it is cooled by radiation losses and by mixing with stellar ejecta at characteristic temperature ~ T_* ~ 10⁷ K, naturally creating the observed positive temperature gradient within ~ 50 kpc. All known E galaxy temperature profiles are positive (Figure 2b) within several R_e and must therefore contain hot circumstellar gas, but when those with very small X-ray images are observed (e.g. NGC 4374: Mathews & Brighenti 1998), it is possible that dT / dr will be negative as in the "isolated" reference model. (3) If the iron abundance in the inflowing circumgalactic gas is z_Fe / z_Fe, ~ 0.3 - 0.4, typical of external regions in groups and clusters, then as the inflowing gas mixes with supernova ejecta, the mean abundance z_Fe / z_Fe, ~ 1 - 2 at r ~ 10 kpc is closer to observed values. The beneficial effect of these improvements, taken together, provide support for subsonic inflow as in classical cooling flow theory.

Central Mass Difficulties: Our reference solution has serious problems near the origin. The amount of gas that has cooled there by time t_n, M_cold = 37 × 10⁹ M, far exceeds the mass M_bh ~ 0.56 - 2.6 × 10⁹ M of the central black hole observed in NGC 4472 (e.g. Magorrian et al. 1998; Merritt & Ferrarese 2001) and would cause the central stellar velocity dispersion to exceed the observed value. In standard cooling flows in luminous E galaxies, with or without circumgalactic gas, the mass of cooled gas, M_cold, is several times greater than the total mass of hot gas at t_n. Although most of the cooled mass M_cold is formed at early times (_* t^-1.3) when our understanding of galactic evolution is uncertain, at the current cooling rate for the reference flow, 1.1 M yr^-1, M_cold and M_bh become equal after only ~ 2 Gyrs. M_cold can also be reduced by supernova driven galactic winds at early times; this may occur even before the E galaxy formed by mergers. If the reference model is begun gas-free at a much later time t_in = 5 Gyrs (redshift z ~ 1.25 for H₀ = 70, _m = 0.3 and = 0.7), then M_cold = 7.7 × 10⁹ M is reduced but still exceeds M_bh - the problem of excessive M_cool does not go away easily.

Compact, luminous X-ray emission is expected as hot interstellar gas flows toward the central supermassive black holes in E galaxies (Fabian & Canizares 1988). In our reference flow, even if the potential energy of the black hole is ignored, the X-ray luminosity of gas cooling by thermal emission at the very center of the flow, L_{x, bol}(r = 0, t_n) (5k T / 2 µ m_p) (0) 10⁴¹ T₇( / M yr) ~ 10⁴¹ ergs s^-1, is comparable to L_{x, bol} from the rest of the flow, in flagrant violation of observations. Attempts to detect compact X-ray sources in giant E galaxies have been remarkably unsuccessful (e.g. Fabian & Rees 1995; Reynolds et al. 1996; Di Matteo et al. 2000; Roberts & Warwick 2000; Loewenstein et al. 2001; Sulkanen & Bregman 2001). This emission shortfall is usually expressed in terms of the luminosity L c² of spherical Bondi accretion onto a mass point, 4 c^-3(G M_bh)², where is the density of distant gas at rest and c 370T₇^1/2 km s^-1 is the isothermal sound speed in this gas. If energy is produced with efficiency = 0.1, the expected luminosity L ~ c² ~ 6 × 10⁴⁴ ( / 0.1) n_e T₇^-3/2 (M_bh / 10⁹ M)², is similar to a quasar. Central X-ray emission from Chandra observations of NGC 6166 (Di Matteo et al. 2001) and M87 (Di Matteo et al. 2003), where nuclear X-ray sources are observed, indicate ~ 10^-4. This low efficiency is within the radiation-reducing capability of advection dominated accretion flows (ADAFs) (Rees et al. 1982; Narayan & Yi 1995; Abramowicz et al. 1995). The in M87 and NGC 6166 may also be reduced below the Bondi rate by occasional AGN heating. In addition, some of the accreting mass and energy may be redirected to kinetic flow along a jet (Blandford & Begelman 1999) which for M87 is ~ 10⁴⁴ erg s^-1. Recently Loewenstein et al (2001) examined Chandra images of several bright E galaxies (NGC 1399, NGC 4472, and NGC 4636) and found no evidence of compact nuclear X-ray emission in the galactic cores, indicating 10^-5. Either the radiative efficiency is incredibly low or gas is not arriving at the black hole in Bondi flow. Perhaps the gas is outflowing in this region or heated in some way by the black hole; these possibilities would be compatible with the flat density gradient observed in the central few kpc of M87 (Di Matteo et al. 2003) that is difficult to produce with inflowing or static solutions.

Mass Dropout: The traditional device to avoid huge central masses of cooled gas and central inflows at t_n has been to assume that the cooling is somehow spread over a large range of radius. To accomplish this, an ad hoc "dropout" term is added to the right hand side of Equation (3), - q / t_cool, where q is a dimensionless parameter (e.g. Fabian, Nulsen & Canizares 1984a; White & Sarazin 1987; Sarazin & Ashe 1989; Kritsuk 1992). This term is designed to force the gas to cool at any radius in proportion to the local gas density divided by the local cooling time at constant pressure, t_cool = 5 m_pk T / 2 µ . For constant q the rate of cooling dropout, q / t_cool n_e², is concentrated toward the galactic center, but q can also be assumed to vary with galactic radius. Sarazin & Ashe (1989) showed that models with q 1 fit the X-ray data reasonably well. It is interesting to estimate the value of q that just balances mass loss from stars in Equation (3), q = (t_cool / ) _{* *} 0.4 where T = 10⁷ K is assumed and we use 8.54 × 10^-20n_e² from Figure 2a. Therefore, in evolutionary models with uniform q ~ 1 gas is removed from the flow at about the same rate that it is supplied by stars. The flow does not shut down if q > 1, however, since the gas density decreases and q / t_cool ² becomes less effective; the total mass of cooled gas is quite independent of q.

In column 2 of Figure 5 we plot the density and temperature using reference model parameters but including the dropout term in Equation (3) with q = 1. One of the historical motivations for dropout was to avoid the central rise in gas density in cooling flow models, but in our experience dropout does not completely solve this difficulty as seen in Figure 5. In this dropout solution the mass of cooled gas, M_cold = 3.8 × 10¹⁰ M, is almost the same as in the reference solution, but only a small fraction cools at the origin. In flows with mass dropout the gas is multiphase everywhere, i.e. some gas cools in pressure equilibrium at every radius and passes through a continuum of higher densities and lower temperatures. The additional emission from these cooling regions, if they exist, is substantial and must be added to the emission of the smooth background gas that radiates in the normal way. Consequently, the observed or apparent gas density is higher and the temperature lower than that of the smooth background. The apparent density profile n_e(r) in column 2 of Figure 5 agrees much better with the data for NGC 4472 than the reference model (q = 0) in column 1. Adding circumgalactic gas would improve the agreement further.

If the cooled gas forms into a spatially extended population of optically dark (dwarf) stars, as often assumed, then the stellar mass to light ratio would vary with galactic radius. In some cases this dark mass can thicken and distort the fundamental plane beyond observed limits (Mathews & Brighenti 2000). But in the high pressure environment of galactic flows, stable Bonner-Ebert spheres at 10⁴ K have masses 2M, and this may also be the maximum mass of any stars that form (Mathews & Brighenti 1999a); because these stars are optically luminous, their influence on the fundamental plane is lessened. Young stars in this mass range could explain the high stellar H features that are commonly observed in giant E galaxies (Mathews & Brighenti 1999b; Terlevich & Forbes 2002).

Another historic difficulty with the dropout hypothesis is that infinitesimal perturbations in the gas density do not develop into full blown thermal instabilities (e.g. Balbus 1991). Loewenstein (1989) showed that small (coherent!) density perturbations oscillate radially in the nearly static hot gas atmosphere with very little overdensity on average and do not cool appreciably faster than the ambient undisturbed gas. Computational studies of the gas dynamics of initially overdense regions in cooling flows (Hattori & Habe 1990; Yoshida, Habe & Hattori 1991; Malagoli, Rosner & Fryxell 1990; Reale et al. 1991; Hattori, Yoshida & Habe 1995) indicate that runaway thermal instabilities are not expected unless the initial perturbation amplitude is very large, / 1. However, in recent 2D calculations of AGN heated flows spatially distributed cooling appeared spontaneously near the outer boundary of the convective region (Kritsuk, Plewa & Müller 2001) and also in non-linear compressions in convective regions (Brighenti & Mathews 2002b).

Nevertheless, intermediate (multiphase) temperatures, an essential outcome of radiative cooling and mass dropout, are not supported by XMM X-ray spectra of galactic scale flows (NGC 4636: Xu et al. 2002; NGC 5044: Buote et al. 2003a; NGC 1399: Buote 2002; M87: Molendi & Pizzolato 2001). Likewise, in cluster scale flows there is no evidence for gas cooling below ~ 1 - 2 keV (Peterson et al. 2001; Tamura et al. 2001; Kaastra et al. 2001; Molendi & Pizzolato 2001; Böhringer et al. 2002; Matsushita et al. 2002). These astonishing null results have led to many speculations, discussed below, but at present no single explanation is generally accepted.

Transition to Winds: Clearly, it could be helpful if the gas flowed out rather than in, but what additional heating is required to drive a wind at time t_n? To answer this question, we heated the gas by increasing the Type Ia supernova rate in NGC 4472 above the reference value SNu(t_n) = 0.06 SNu and repeated the calculation with all other parameters (including s) unchanged. The transition to a wind is abrupt. As seen in column 3 of Figure 5, for SNu(t_n) = 0.18 the temperature and density profiles at t_n are almost identical to the reference solution, although M_cold = 2.5 × 10¹⁰ M, M_hot = 2.4 × 10¹⁰ M and L_{x, bol} = 1.0 × 10⁴² erg s^-1 are all slightly lower due to outflows at early times. At time t_n the gas is flowing inward at all radii. However, a further small increase to SNu(t_n) = 0.25 produces a strong global wind at t_n with very low gas density at all radii and L_{x, bol} drops to 1.9 × 10⁴¹ erg s^-1. No known galaxy has density, temperature and abundance profiles like those for the SNu(t_n) = 0.25 solution in Figure 5. Outflows generally require finely-tuned heating. More realistic galactic flows with additional circumgalactic gas require a much larger SNu(t_n) to drive an outflow by t_n. Outflows may be common in low luminosity ellipticals, L_b L_{B, crit}, and spiral bulges where the hot gas is difficult to observe. If the reference Type Ia rate SNu(t_n) = 0.06 SNu is applied to elliptical galaxies that are 0.3 as luminous as NGC 4472, outflows at t_n are easy to generate.

Past Supernova Rate: Next we describe several flows at t_n for a variety of past supernova rates SNu(t) t^-s, by varying the index s from 0 to 2, keeping SNu(t_n) = 0.06 fixed. In row 3, column 4 of Figure 5 we show the current (t = t_n) hot gas iron abundance profiles for flows with s = 0, 1.5 and 2. The temperature and density profiles at t_n change little over this range of s. M_cold decreases by about 4.5 as s increases from 0 to 2 because of supernova-driven outflows at early times. L_{x, bol}(t_n) only decreases by 40 percent as s varies from 0 to 2. Recall that s > 1.3 (s < 1.3) is a necessary condition for supernova driven winds to occur at early (late) times.

Ciotti et al. (1991) considered evolutionary models with s = 1.5 and SNu(t_n) = 0.11 - 0.22 SNu, so that outflows and winds occur at early times, thereby reducing M_cool(t_n). They also assumed that the fraction of galactic mass in dark halos varies among elliptical galaxies with similar L_B. As a result, the model ellipticals described by Ciotti et al. are at the present time in different phases of a transition from outflow (low L_{x, bol} / L_B) to cooling inflow (high L_{x, bol} / L_B) and they interpret this as an explanation for the large scatter in the L_x, L_B plot. However, for the same range of supernova parameters, the variations in L_x / L_B would be greatly reduced if circumgalactic gas had been included. Furthermore, the iron abundance at t_n is strongly linked to the past supernova rate (Loewenstein & Mathews 1991; Brighenti & Mathews 1999b). Type Ia rates required to drive winds at early times deposit too much iron in the hot gas by time t_n. The iron abundance for our s = 1.5 galaxy in Figure 5 is ~ 3.5 solar throughout the hot gas. This high abundance cannot be satisfactorily reduced by mixing with inflowing circumgalactic gas (column 1, Figure 5). We conclude that the transient evolution from supernova-driven winds to inflows is unlikely to explain the large scatter in the L_x, L_B plot for massive ellipticals (L_B 3 × 10¹⁰ L_B, ).

Additional Parameters: Finally, we note several additional parameters that have some influence on the solutions at time t_n = 13 Gyrs. Varying the (uniform) stellar temperature T_* from 6 × 10⁶ K (the reference flow value) to 2 × 10⁶ K or 18 × 10⁶ K (but keeping the stellar mass fixed) leaves n_e(r) and T(r) essentially unchanged. Matsushita (2001) argues that L_x and the hot gas temperature in E galaxies without circumgalactic gas can be explained by kinematical heating of the gas by stellar mass loss. However, the kinematic temperature T_* of mass lost from orbiting stars is essentially the same as the hot gas temperature, i.e., both are determined by the same gravitational potential. Altering the radiative cooling coefficient (T) by factors 3 or 1/3 has no appreciable effect on T(r) but the gas density increases slightly with decreasing . If = 0, as if some source of heating perfectly balances radiative cooling at every radius, then there is no radial flow and no gas cools at any radius. But in this strange solution the gas density becomes very large and the density gradient steepens ( _*) because a larger pressure gradient is required to support the denser, nearly static atmosphere. Decreasing the mass of the NFW halo from the reference value M_h = 4 × 10¹³ M to M_h = 5 × 10¹² M leaves n_e(r) essentially unchanged but T(r) is ~ 20 percent lower at r = 10 kpc. For M_h = 10¹² M, however, a mild galactic wind sets in at late times and the density and temperature are both significantly lower. In this last solution L_{x, bol} is ~ 30 times lower than the reference value and comparable to the luminosity of discrete stellar X-ray sources in NGC 4472, L_x,* 3 × 10⁴⁰ erg s^-1 (Figure 1). It is also interesting to vary the stellar mass loss rate _*, simulating a situation in which not all of the gas ejected from stars goes into the hot phase. When _*(t_n) is reduced by 2, holding _sn at its reference value, the total mass of cooled gas M_cold and L_x are both lowered by 2. The gas temperature within ~ 40 kpc is lower by ~ 1.4, but the total mass of hot gas M_hot = 1.1 × 10¹⁰ M is almost unchanged. If _*(t_n) is lowered further, a wind develops by time t_n.