Observations of the cosmic microwave background [348] have confirmed the notion that the present large-scale structure in the Universe originated from small-amplitude density fluctuations at early cosmic times. Due to the natural instability of gravity, regions that were denser than average collapsed and formed bound halos, first on small spatial scales and later on larger and larger scales. At each snapshot of this cosmic evolution, the abundance of collapsed halos, whose masses are dominated by cold dark matter, can be computed from the initial conditions using numerical simulations and can be understood using approximate analytic models [292, 52]. The common understanding of galaxy formation is based on the notion that the constituent stars formed out of the gas that cooled and subsequently condensed to high densities in the cores of some of these halos [379].
The standard analytic model for the abundance of halos
[292,
52]
considers the small density fluctuations at some early,
initial time, and attempts to predict the number of halos that will
form at some later time corresponding to a redshift z. First, the
fluctuations are extrapolated to the present time using the growth
rate of linear fluctuations, and then the average density is computed
in spheres of various sizes. Whenever the overdensity (i.e., the
density perturbation in units of the cosmic mean density) in a sphere
rises above a critical threshold
c(z),
the corresponding
region is assumed to have collapsed by redshift z, forming a halo
out of all the mass that had been included in the initial spherical
region. In analyzing the statistics of such regions, the model
separates the contribution of large-scale modes from that of
small-scale density fluctuations. It predicts that galactic halos will
form earlier in regions that are overdense on large scales
[190,
19,
97,
258],
since these regions already start out from an
enhanced level of density, and small-scale modes need only supply the
remaining perturbation necessary to reach
c(z).
On the other hand, large-scale voids should contain a reduced number of
halos at high redshift. In this way, the analytic model describes the
clustering of massive halos.
As gas falls into a dark matter halo, it can fragment into stars only if its virial temperature is above 104 K for cooling mediated by atomic transitions [or ~ 500 K for molecular H2 cooling; see Fig. 20]. The abundance of dark matter halos with a virial temperature above this cooling threshold declines sharply with increasing redshift due to the exponential cutoff in the abundance of massive halos at early cosmic times. Consequently, a small change in the collapse threshold of these rare halos, due to mild inhomogeneities on much larger spatial scales, can change the abundance of such halos dramatically. Barkana & Loeb (2004) [27] have shown that the modulation of galaxy formation by long wavelength modes of density fluctuations is therefore amplified considerably at high redshift; the discussion in this section follows their analysis.
Amplification of Density Fluctuations
Galaxies at high redshift are believed to form in all halos above some
minimum mass Mmin that depends on the efficiency of
atomic and
molecular transitions that cool the gas within each halo. This makes useful
the standard quantity of the collapse fraction
Fcol(Mmin),
which is the fraction of mass in a given volume that is contained in halos
of individual mass Mmin or greater (see
Fig. 13). If
we set Mmin to be the minimum halo mass in which
efficient cooling processes are triggered, then
Fcol(Mmin) is the fraction of
all baryons that reside in galaxies. In a large-scale region of comoving
radius R with a mean overdensity
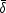R, the
standard result is
[52]
 |
(182) |
where S(R) =
2(R)
is the variance of fluctuations in spheres of radius
R, and S(Rmin) is the variance in
spheres of radius Rmin corresponding to the region at
the initial time that contained a mass
Mmin. In particular, the cosmic mean value of the collapse
fraction is obtained in the limit of R
by setting
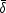R and
S(R) to zero in this expression. Throughout this
section we shall adopt this standard model, known as the extended
Press-Schechter model. Whenever we consider a cubic region, we will
estimate its halo abundance by applying the model to a spherical region of
equal volume. Note also that we will consistently quote values of comoving
distance, which equals physical distance times a factor of (1 + z).
At high redshift, galactic halos are rare and correspond to high peaks in the Gaussian probability distribution of initial fluctuations. A modest change in the overall density of a large region modulates the threshold for high peaks in the Gaussian density field, so that the number of galaxies is exponentially sensitive to this modulation. This amplification of large-scale modes is responsible for the large statistical fluctuations that we find.
In numerical simulations, periodic boundary conditions are usually assumed,
and this forces the mean density of the box to equal the cosmic mean
density. The abundance of halos as a function of mass is then biased in
such a box (see Fig. 65), since a similar
region in the real Universe will have a distribution of different
overdensities
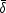R.
At high redshift, when galaxies correspond to high
peaks, they are mostly found in regions with an enhanced large-scale
density. In a periodic box, therefore, the total number of galaxies is
artificially reduced, and the relative abundance of galactic halos with
different masses is artificially tilted in favor of lower-mass halos. Let
us illustrate these results for two sets of parameters, one corresponding
to the first galaxies and early reionization (z = 20) and the
other to the
current horizon in observations of galaxies and late reionization
(z = 7). Let us consider a resolution equal to that of
state-of-the-art cosmological simulations that include gravity and gas
hydrodynamics. Specifically, let us assume that the total number of dark
matter particles in the simulation is N = 3243, and
that the smallest halo that can form a galaxy must be resolved into 500
particles;
[349]
showed that this resolution is necessary in order to
determine the star formation rate in an individual halo reliably to within
a factor of two. Therefore, if we assume that halos that cool via molecular
hydrogen must be resolved at z = 20 (so that
Mmin = 7 × 105
M
), and
only those that cool via atomic transitions must be
resolved at z = 7 (so that Mmin = 108
M), then
the maximum
box sizes that can currently be simulated in hydrodynamic comological
simulations are lbox = 1 Mpc and
lbox = 6 Mpc at these two redshifts, respectively.
 |
Figure 65. Bias in the halo mass
distribution in simulations. Shown is the
amount of mass contained in all halos of individual mass
Mmin or
greater, expressed as a fraction of the total mass in a given volume. This
cumulative fraction Fcol(Mmin) is
illustrated as a function
of the minimum halo mass Mmin. We consider two cases
of redshift and simulation box size, namely z = 7,
lbox = 6 Mpc (upper curves),
and z = 20, lbox = 1 Mpc (lower curves). At
each redshift, we
compare the true average distribution in the Universe (dotted curve) to the
biased distribution (solid curve) that would be measured in a simulation
box with periodic boundary conditions (for which
|
At each redshift we only consider cubic boxes large enough so that the
probability of forming a halo on the scale of the entire box is
negligible. In this case,
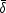R is
Gaussian distributed with
zero mean and variance S(R), since the no-halo condition
[S(R)]1/2 <<
c(z)
implies that at redshift z the perturbation on the scale R
is still in the linear regime. We can then calculate the probability
distribution of collapse fractions in a box of a given size (see
Fig. 66). This distribution corresponds to a
real variation in the
fraction of gas in galaxies within different regions of the Universe at a
given time. In a numerical simulation, the assumption of periodic boundary
conditions eliminates the large-scale modes that cause this cosmic
scatter. Note that Poisson fluctuations in the number of halos within the
box would only add to the scatter, although the variations we have
calculated are typically the dominant factor. For instance, in our two
standard examples, the mean expected number of halos in the box is 3 at
z = 20 and 900 at z = 7, resulting in Poisson fluctuations
of a factor of
about 2 and 1.03, respectively, compared to the clustering-induced scatter
of a factor of about 16 and 2 in these two cases.
 |
Figure 66. Probability distribution within
a small volume of the total
mass fraction in galactic halos. The normalized distribution of the
logarithm of this fraction
Fcol(Mmin) is shown for two
cases: z = 7, lbox = 6 Mpc,
Mmin = 108
M |
Within the extended Press-Schechter model, both the numerical bias and the
cosmic scatter can be simply described in terms of a shift in the redshift
(see Fig. 67). In general, a region of radius
R with a mean overdensity
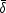R will
contain a different collapse fraction than the cosmic mean value at a
given redshift z. However, at some wrong redshift z +
z this small
region will contain the cosmic mean
collapse fraction at z. At high redshifts (z > 3), this
shift in redshift was derived by Barkana & Loeb
[27]
from equation (182) [and was already mentioned in Eq. (168)]
 |
(183) |
where 0
c(z) /
(1 + z) is approximately constant at high redshifts
[283],
and equals 1.28 for
the standard cosmological parameters (with its deviation from the
Einstein-de Sitter value of 1.69 resulting from the existence of a
cosmological constant). Thus, in our two examples, the bias is -2.6 at
z = 20 and -0.4 at z = 7, and the one-sided
1 - scatter is 2.4 at
z = 20 and 1.2 at z = 7.
 |
Figure 67. Cosmic scatter and numerical
bias, expressed as the change in redshift needed to get the correct
cosmic mean of the collapse fraction. The plot shows the
1- |
Matching Numerical Simulations
Next we may develop an improved model that fits the results
of numerical simulations more accurately. The model constructs the
halo mass distribution (or mass function); cumulative quantities such
as the collapse fraction or the total number of galaxies can then be
determined from it via integration. We first define
f(c(z), S)
dS to be the mass fraction contained at z within halos
with mass in
the range corresponding to S to S + d S.
As derived earlier, the Press-Schechter halo abundance is
 |
(184) |
where dn is the comoving number density of halos with masses in the range M to M + dM, and
 |
(185) |
where 
=
c(z)
/ S1/2 is the
number of standard deviations that the critical collapse overdensity
represents on the mass scale M corresponding to the variance
S.
However, the Press-Schechter mass function fits numerical simulations only roughly, and in particular it substantially underestimates the abundance of the rare halos that host galaxies at high redshift. The halo mass function of [333] [see also [334]] adds two free parameters that allow it to fit numerical simulations much more accurately [188]. These N-body simulations followed very large volumes at low redshift, so that cosmic scatter did not compromise their accuracy. The matching mass function is given by
 |
(186) |
with best-fit parameters [335] a' = 0.75 and q' = 0.3, and where normalization to unity is ensured by taking A' = 0.322.
In order to calculate cosmic scatter we must determine the biased halo
mass function in a given volume at a given mean density. Within the
extended Press-Schechter model
[52],
the halo mass distribution in a region of comoving radius R with
a mean overdensity
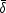R is
given by
 |
(187) |
The corresponding collapse fraction in this case is given simply by eq. (182). Despite the relatively low accuracy of the Press-Schechter mass function, the relative change is predicted rather accurately by the extended Press-Schechter model. In other words, the prediction for the halo mass function in a given volume compared to the cosmic mean mass function provides a good fit to numerical simulations over a wide range of parameters [258, 77].
For the improved model (derived in [27]), we adopt a hybrid approach that combines various previous models with each applied where it has been found to closely match numerical simulations. We obtain the halo mass function within a restricted volume by starting with the Sheth-Torme formula for the cosmic mean mass function, and then adjusting it with a relative correction based on the extended Press-Schechter model. In other words, we set
 |
(188) |
As noted, this model is based on fits to simulations at low redshifts, but we can check it at high redshifts as well. Figure 68 shows the number of galactic halos at z ~ 15-30 in two numerical simulations run by [402], and our predictions given the cosmological input parameters assumed by each simulation. The close fit to the simulated data (with no additional free parameters) suggests that our hybrid model (solid lines) improves on the extended Press-Schechter model (dashed lines), and can be used to calculate accurately the cosmic scatter in the number of galaxies at both high and low redshifts. The simulated data significantly deviate from the expected cosmic mean [eq. (186), shown by the dotted line], due to the artificial suppression of large-scale modes outside the simulated box.
 |
Figure 68. Halo mass function at high
redshift in a 1 Mpc box at the
cosmic mean density. The prediction (solid lines) of
the hybrid model of Barkana & Loeb (2004)
[27]
is compared with the number of halos above mass 7 × 105
M |
As an additional example, we consider the highest-resolution first
star simulation
[5],
which used lbox = 128 kpc and
Mmin = 7 × 105
M. The
first star forms within
the simulated volume when the first halo of mass Mmin or
larger collapses within the box. To compare with the simulation, we
predict the redshift at which the probability of finding at least one
halo within the box equals 50%, accounting for Poisson
fluctuations. We find that if the simulation formed a population of
halos corresponding to the correct cosmic average [as given by
eq. (186)], then the first star should have formed already at
z = 24.0. The first star actually formed in the simulation box
only at z = 18.2
[5].
Using eq. (188) we can account for
the loss of large-scale modes beyond the periodic box, and predict a
first star at z = 17.8, a close match given the large Poisson
fluctuations introduced by considering a single galaxy within the box.
The artificial bias in periodic simulation boxes can also be seen in the results of extensive numerical convergence tests carried out by [349]. They presented a large array of numerical simulations of galaxy formation run in periodic boxes over a wide range of box size, mass resolution, and redshift. In particular, we can identify several pairs of simulations where the simulations in each pair have the same mass resolution but different box sizes; this allows us to separate the effect of large-scale numerical bias from the effect of having poorly-resolved individual halos.
Implications
(i) The nature of reionization
A variety of papers in the literature
[13,
138,
330,
171,
152,
23,
224]
maintain that reionization ended with a fast,
simultaneous, overlap stage throughout the Universe. This view has been
based on simple arguments and has been supported by numerical simulations
with small box sizes. The underlying idea was that the ionized hydrogen (H
II ) regions of individual sources began to overlap when the typical size
of each H II bubble became comparable to the distance between nearby
sources. Since these two length scales were comparable at the critical
moment, there is only a single timescale in the problem - given by the
growth rate of each bubble - and it determines the transition time between
the initial overlap of two or three nearby bubbles, to the final stage
where dozens or hundreds of individual sources overlap and produce large
ionized regions. Whenever two ionized bubbles were joined, each point
inside their common boundary became exposed to ionizing photons from both
sources, reducing the neutral hydrogen fraction and allowing ionizing
photons to travel farther before being absorbed. Thus, the ionizing
intensity inside H II regions rose rapidly, allowing those regions to
expand into high-density gas that had previously recombined fast enough to
remain neutral when the ionizing intensity had been low. Since each bubble
coalescence accelerates the process, it has been thought that the overlap
phase has the character of a phase transition and occurs rapidly. Indeed,
the simulations of reionization
[152]
found that the
average mean free path of ionizing photons in the simulated volume rises by
an order of magnitude over a redshift interval
z = 0.05 at
z = 7.
These results imply that overlap is still expected to occur rapidly, but only in localized high-density regions, where the ionizing intensity and the mean free path rise rapidly even while other distant regions are still mostly neutral. In other words, the size of the bubble of an individual source is about the same in different regions (since most halos have masses just above Mmin), but the typical distance between nearby sources varies widely across the Universe. The strong clustering of ionizing sources on length scales as large as 30 - 100 Mpc introduces long timescales into the reionization phase transition. The sharpness of overlap is determined not by the growth rate of bubbles around individual sources, but by the ability of large groups of sources within overdense regions to deliver ionizing photons into large underdense regions.
Note that the recombination rate is higher in overdense regions because of their higher gas density. These regions still reionize first, though, despite the need to overcome the higher recombination rate, since the number of ionizing sources in these regions is increased even more strongly as a result of the dramatic amplification of large-scale modes discussed earlier.
(ii) Limitations of current simulations
The shortcomings of current simulations do not amount simply to a shift of
~ 10% in redshift and the elimination of scatter. The effect
mentioned above can be expressed in terms of a shift in redshift only
within the context of the extended Press-Schechter model, and only if the
total mass fraction in galaxies is considered and not its distribution as a
function of galaxy mass. The halo mass distribution should still have the
wrong shape, resulting from the fact that
z depends on
Mmin. A self-contained numerical simulation must
directly evolve a very large volume.
Another reason that current simulations are limited is that at high redshift, when galaxies are still rare, the abundance of galaxies grows rapidly towards lower redshift. Therefore, a ~ 10% relative error in redshift implies that at any given redshift around z ~ 10 - 20, the simulation predicts a halo mass function that can be off by an order of magnitude for halos that host galaxies (see Fig. 68). This large underestimate suggests that the first generation of galaxies formed significantly earlier than indicated by recent simulations. Another element missed by simulations is the large cosmic scatter. This scatter can fundamentally change the character of any observable process or feedback mechanism that depends on a radiation background. Simulations in periodic boxes eliminate any large-scale scatter by assuming that the simulated volume is surrounded by identical periodic copies of itself. In the case of reionization, for instance, current simulations neglect the collective effects described above, whereby groups of sources in overdense regions may influence large surrounding underdense regions. In the case of the formation of the first stars due to molecular hydrogen cooling, the effect of the soft ultraviolet radiation from these stars, which tends to dissociate the molecular hydrogen around them [170, 303, 272], must be reassessed with cosmic scatter included.
(iii) Observational consequences
The spatial fluctuations that we have calculated also affect current and
future observations that probe reionization or the galaxy population at
high redshift. For example, there are a large number of programs searching
for galaxies at the highest accessible redshifts (6.5 and beyond) using
their strong Ly
emission
[184,
301,
244,
202].
These programs
have previously been justified as a search for the reionization redshift,
since the intrinsic emission should be absorbed more strongly by the
surrounding IGM if this medium is neutral. For any particular source, it
will be hard to clearly recognize this enhanced absorption because of
uncertainties regarding the properties of the source and its radiative and
gravitational effects on its surroundings
[24,
26,
312].
However, if the luminosity function of galaxies that emit
Ly can be observed, then
faint sources, which do
not significantly affect their environment, should be very strongly
absorbed in the era before reionization. Reionization can then be detected
statistically through the sudden jump in the number of faint sources
[246].
The above results alter the expectation for such
observations. Indeed, no sharp "reionization redshift" is
expected. Instead, a
Ly luminosity function
assembled from a large
area of the sky will average over the cosmic scatter of
z ~
1 - 2 between different regions, resulting in a smooth evolution of the
luminosity function over this redshift range. In addition, such a survey
may be biased to give a relatively high redshift, since only the most
massive galaxies can be detected, and as we have shown, these galaxies will
be concentrated in overdense regions that will also get reionized
relatively early.
The distribution of ionized patches during reionization will likely be probed by future observations, including small-scale anisotropies of the cosmic microwave background photons that are rescattered by the ionized patches [8, 162, 313], and observations of 21 cm emission by the spin-flip transition of the hydrogen in neutral regions [366, 75, 142]. Previous analytical and numerical estimates of these signals have not included the collective effects discussed above, in which rare groups of massive galaxies may reionize large surrounding areas. The transfer of photons across large scales will likely smooth out the signal even on scales significantly larger than the typical size of an H II bubble due to an individual galaxy. Therefore, even the characteristic angular scales that are expected to show correlations in such observations must be reassessed.
The cosmic scatter also affects observations in the present-day Universe that depend on the history of reionization. For instance, photoionization heating suppresses the formation of dwarf galaxies after reionization, suggesting that the smallest galaxies seen today may have formed prior to reionization [73, 344, 37]. Under the popular view that assumed a sharp end to reionization, it was expected that denser regions would have formed more galaxies by the time of reionization, possibly explaining the larger relative abundance of dwarf galaxies observed in galaxy clusters compared to lower-density regions such as the Local Group of galaxies [369, 38]. The above results undercut the basic assumption of this argument and suggest a different explanation. Reionization occurs roughly when the number of ionizing photons produced starts to exceed the number of hydrogen atoms in the surrounding IGM. If the processes of star formation and the production of ionizing photons are equally efficient within galaxies that lie in different regions, then reionization in each region will occur when the collapse fraction reaches the same critical value, even though this will occur at different times in different regions. Since the galaxies responsible for reionization have the same masses as present-day dwarf galaxies, this estimate argues for a roughly equal abundance of dwarf galaxies in all environments today. This simple picture is, however, modified by several additional effects. First, the recombination rate is higher in overdense regions at any given time, as discussed above. Furthermore, reionization in such regions is accomplished at an earlier time when the recombination rate was higher even at the mean cosmic density; therefore, more ionizing photons must be produced in order to compensate for the enhanced recombination rate. These two effects combine to make overdense regions reionize at a higher value of Fcol than underdense regions. In addition, the overdense regions, which reionize first, subsequently send their extra ionizing photons into the surrounding underdense regions, causing the latter to reionize at an even lower Fcol. Thus, a higher abundance of dwarf galaxies today is indeed expected in the overdense regions.
The same basic effect may be even more critical for understanding the
properties of large-scale voids, 10 - 30 Mpc regions in the present-day
Universe with an average mass density that is well below the cosmic
mean. In order to predict their properties, the first step is to
consider the abundance of dark matter halos within them. Numerical
simulations show that voids contain a lower relative abundance of rare
halos
[249,
82,
39],
as expected from the raising of the
collapse threshold for halos within a void. On the other hand,
simulations show that voids actually place a larger fraction of their
dark matter content in dwarf halos of mass below 1010
M
[157].
This can be understood within the extended
Press-Schechter model. At the present time, a typical region in the
Universe fills halos of mass 1012
M and
higher with most
of the dark matter, and very little is left over for isolated dwarf
halos. Although a large number of dwarf halos may have formed at early
times in such a region, the vast majority later merged with other
halos, and by the present time they survive only as substructure
inside much larger halos. In a void, on the other hand, large halos
are rare even today, implying that most of the dwarf halos that formed
early within a void can remain as isolated dwarf halos till the
present. Thus, most isolated dwarf dark matter halos in the present
Universe should be found within large-scale voids
[25].
However, voids are observed to be rather deficient in dwarf galaxies as
well as in larger galaxies on the scale of the Milky Way mass of ~
1012
M
[200,
120,
285].
A deficit of large galaxies
is naturally expected, since the total mass density in the void is
unusually low, and the fraction of this already low density that assembles
in large halos is further reduced relative to higher-density regions. The
absence of dwarf galaxies is harder to understand, given the higher
relative abundance expected for their host dark matter halos. The standard
model for galaxy formation may be consistent with the observations if some
of the dwarf halos are dark and do not host stars. Large numbers of dark
dwarf halos may be produced by the effect of reionization in suppressing
the infall of gas into these halos. Indeed, exactly the same factors
considered above, in the discussion of dwarf galaxies in clusters compared
to those in small groups, apply also to voids. Thus, the voids should
reionize last, but since they are most strongly affected by ionizing
photons from their surroundings (which have a higher density than the voids
themselves), the voids should reionize when the abundance of galaxies
within them is relatively low.
Acknowledgements
I thank my young collaborators with whom my own research in this field was accomplished: Dan Babich, Rennan Barkana, Volker Bromm, Benedetta Ciardi, Daniel Eisenstein, Steve Furlanetto, Zoltan Haiman, Rosalba Perna, Stuart Wyithe, and Matias Zaldarriaga. I thank Donna Adams for her highly professional assistance with the latex file, and Dan Babich & Matt McQuinn for their helpful comments on the manuscript.
CDM
model of
[