9. THE FRONTIER OF 21cm COSMOLOGY

9.1. Mapping Hydrogen Before Reionization

The small residual fraction of free electrons after cosmological recombination coupled the temperature of the cosmic gas to that of the cosmic microwave background (CMB) down to a redshift, z ~ 200 [284]. Subsequently, the gas temperature dropped adiabatically as T_gas (1 + z)² below the CMB temperature T (1 + z). The gas heated up again after being exposed to the photo-ionizing ultraviolet light emitted by the first stars during the reionization epoch at z < 20. Prior to the formation of the first stars, the cosmic neutral hydrogen must have resonantly absorbed the CMB flux through its spin-flip 21cm transition [131, 323, 367, 404]. The linear density fluctuations at that time should have imprinted anisotropies on the CMB sky at an observed wavelength of = 21.12[(1 + z) / 100] meters. We discuss these early 21cm fluctuations mainly for pedagogical purposes. Detection of the earliest 21cm signal will be particularly challenging because the foreground sky brightness rises as ^2.5 at long wavelengths in addition to the standard ^1/2 scaling of the detector noise temperature for a given integration time and fractional bandwidth. The discussion in this section follows Loeb & Zaldarriaga (2004) [226].

Figure 53. The 21cm transition of hydrogen. The higher energy level the spin of the electron (e-) is aligned with that of the proton (p+). A spin flip results in the emission of a photon with a wavelength of 21cm (or a frequency of 1420MHz).

We start by calculating the history of the spin temperature, T_s, defined through the ratio between the number densities of hydrogen atoms in the excited and ground state levels, n₁ / n₀ = (g₁/ g₀)exp{-T_* / T_s},

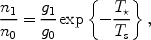(154)

where subscripts 1 and 0 correspond to the excited and ground state levels of the 21cm transition, (g₁ / g₀) = 3 is the ratio of the spin degeneracy factors of the levels, n_H = (n₀ + n₁) (1 + z)³ is the total hydrogen density, and T_* = 0.068K is the temperature corresponding to the energy difference between the levels. The time evolution of the density of atoms in the ground state is given by,

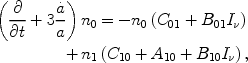(155)

where a(t) = (1 + z)^-1 is the cosmic scale factor, A's and B's are the Einstein rate coefficients, C's are the collisional rate coefficients, and I is the blackbody intensity in the Rayleigh-Jeans tail of the CMB, namely I = 2kT / ² with = 21 cm [306]. Here a dot denotes a time-derivative. The 0 1 transition rates can be related to the 1 0 transition rates by the requirement that in thermal equilibrium with T_s = T = T_gas, the right-hand-side of Eq. (155) should vanish with the collisional terms balancing each other separately from the radiative terms. The Einstein coefficients are A₁₀ = 2.85 × 10^-15 s^-1, B₁₀ = (³ / 2hc) A₁₀ and B₀₁ = (g₁ / g₀)B₁₀ [131, 306]. The collisional de-excitation rates can be written as C₁₀ = 4/3 (1 - 0) n_H, where (1 - 0) is tabulated as a function of T_gas [11, 406].

Equation (155) can be simplified to the form,

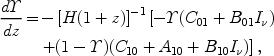(156)

where n₀ / n_H, H H₀ (_m)^1/2(1 + z)^3/2 is the Hubble parameter at high redshifts (with a present-day value of H₀), and _m is the density parameter of matter. The upper panel of Fig. 54 shows the results of integrating Eq. (156). Both the spin temperature and the kinetic temperature of the gas track the CMB temperature down to z ~ 200. Collisions are efficient at coupling T_s and T_gas down to z ~ 70 and so the spin temperature follows the kinetic temperature around that redshift. At much lower redshifts, the Hubble expansion makes the collision rate subdominant relative the radiative coupling rate to the CMB, and so T_s tracks T again. Consequently, there is a redshift window between 30 < z < 200, during which the cosmic hydrogen absorbs the CMB flux at its resonant 21cm transition. Coincidentally, this redshift interval precedes the appearance of collapsed objects [23] and so its signatures are not contaminated by nonlinear density structures or by radiative or hydrodynamic feedback effects from stars and quasars, as is the case at lower redshifts [404].

Figure 54. Upper panel: Evolution of the gas, CMB and spin temperatures with redshift [4]. Lower panel: dTb / dH as function of redshift. The separate contributions from fluctuations in the density and the spin temperature are depicted. We also show dTb / dH a dTb / dH × H, with an arbitrary normalization.

During the period when the spin temperature is smaller than the CMB temperature, neutral hydrogen atoms absorb CMB photons. The resonant 21cm absorption reduces the brightness temperature of the CMB by,

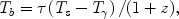(157)

where the optical depth for resonant 21cm absorption is,

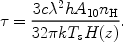(158)

Small inhomogeneities in the hydrogen density _H (n_H - _H) / _H result in fluctuations of the 21cm absorption through two separate effects. An excess of neutral hydrogen directly increases the optical depth and also alters the evolution of the spin temperature. For now, we ignore the additional effects of peculiar velocities (Bharadwaj & Ali 2004 [41]; Barkana & Loeb 2004 [27]) as well as fluctuations in the gas kinetic temperature due to the adiabatic compression (rarefaction) in overdense (underdense) regions [29]. Under these approximations, we can write an equation for the resulting evolution of fluctuations,

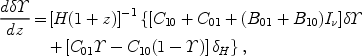(159)

leading to spin temperature fluctuations,

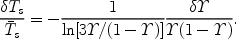(160)

The resulting brightness temperature fluctuations can be related to the derivative,

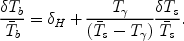(161)

The spin temperature fluctuations T_s / T_s are proportional to the density fluctuations and so we define,

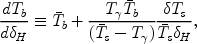(162)

through T_b = (d T_b / d _H) _H. We ignore fluctuations in C_ij due to fluctuations in T_gas which are very small [11]. Figure 54 shows dT_b / d_H as a function of redshift, including the two contributions to dT_b / d_H, one originating directly from density fluctuations and the second from the associated changes in the spin temperature [323]. Both contributions have the same sign, because an increase in density raises the collision rate and lowers the spin temperature and so it allows T_s to better track T_gas. Since _H grows with time as _H a, the signal peaks at z ~ 50, a slightly lower redshift than the peak of dT_b / d_H.

Next we calculate the angular power spectrum of the brightness temperature on the sky, resulting from density perturbations with a power spectrum P(k),

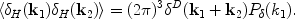(163)

where _H(k) is the Fourier tansform of the hydrogen density field, k is the comoving wavevector, and < … > denotes an ensemble average (following the formalism described in [404]). The 21cm brightness temperature observed at a frequency corresponding to a distance r along the line of sight, is given by

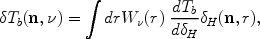(164)

where n denotes the direction of observation, W(r) is a narrow function of r that peaks at the distance corresponding to . The details of this function depend on the characteristics of the experiment. The brightness fluctuations in Eq. 164 can be expanded in spherical harmonics with expansion coefficients a_lm(). The angular power spectrum of map C_l() = < |a_lm()|² > can be expressed in terms of the 3D power spectrum of fluctuations in the density P(k),

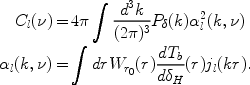(165)

Our calculation ignores inhomogeneities in the hydrogen ionization fraction, since they freeze at the earlier recombination epoch (z ~ 10³) and so their amplitude is more than an order of magnitude smaller than _H at z < 100. The gravitational potential perturbations induce a redshift distortion effect that is of order ~ (H / ck)² smaller than _H for the high - l modes of interest here.

Figure 55 shows the angular power spectrum at various redshifts. The signal peaks around z ~ 50 but maintains a substantial amplitude over the full range of 30 < z < 100. The ability to probe the small scale power of density fluctuations is only limited by the Jeans scale, below which the dark matter inhomogeneities are washed out by the finite pressure of the gas. Interestingly, the cosmological Jeans mass reaches its minimum value, ~ 3 × 10⁴ M, within the redshift interval of interest here which corresponds to modes of angular scale ~ arcsecond on the sky. During the epoch of reionization, photoionization heating raises the Jeans mass by several orders of magnitude and broadens spectral features, thus limiting the ability of other probes of the intergalactic medium, such as the Ly forest, from accessing the same very low mass scales. The 21cm tomography has the additional advantage of probing the majority of the cosmic gas, instead of the trace amount (~ 10^-5) of neutral hydrogen probed by the Ly forest after reionization. Similarly to the primary CMB anisotropies, the 21cm signal is simply shaped by gravity, adiabatic cosmic expansion, and well-known atomic physics, and is not contaminated by complex astrophysical processes that affect the intergalactic medium at z < 30.

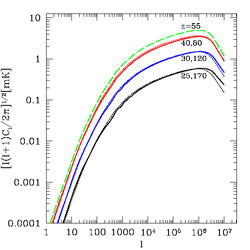Figure 55. Angular power spectrum of 21cm anisotropies on the sky at various redshifts. From top to bottom, z = 55,40,80,30,120,25,170.

Characterizing the initial fluctuations is one of the primary goals of observational cosmology, as it offers a window into the physics of the very early Universe, namely the epoch of inflation during which the fluctuations are believed to have been produced. In most models of inflation, the evolution of the Hubble parameter during inflation leads to departures from a scale-invariant spectrum that are of order 1/N_efold with N_efold ~ 60 being the number of e - folds between the time when the scale of our horizon was of order the horizon during inflation and the end of inflation [218]. Hints that the standard CDM model may have too much power on galactic scales have inspired several proposals for suppressing the power on small scales. Examples include the possibility that the dark matter is warm and it decoupled while being relativistic so that its free streaming erased small-scale power [48], or direct modifications of inflation that produce a cut-off in the power on small scales [192]. An unavoidable collisionless component of the cosmic mass budget beyond CDM, is provided by massive neutrinos (see [198] for a review). Particle physics experiments established the mass splittings among different species which translate into a lower limit on the fraction of the dark matter accounted for by neutrinos of f > 0.3 %, while current constraints based on galaxies as tracers of the small scale power imply f < 12 % [360].

Figure 56 shows the 21cm power spectrum for various models that differ in their level of small scale power. It is clear that a precise measurement of the 21cm power spectrum will dramatically improve current constraints on alternatives to the standard CDM spectrum.

Figure 56. Upper panel: Power spectrum of 21cm anisotropies at z = 55 for a CDM scale-invariant power spectrum, a model with n = 0.98, a model with n = 0.98 and r 1/2 (d2lnP / dln k2) = -0.07, a model of warm dark matter particles with a mass of 1 keV, and a model in which f = 10% of the matter density is in three species of massive neutrinos with a mass of 0.4 eV each. Lower panel: Ratios between the different power spectra and the scale-invariant spectrum.

The sensitivity of an experiment depends strongly on its particular design, involving the number and distribution of the antennae for an interferometer. Crudely speaking, the uncertainty in the measurement of [l(l + 1)C_l / 2]^1/2 is dominated by noise, N, which is controlled by the sky brightness I at the observed frequency [404],

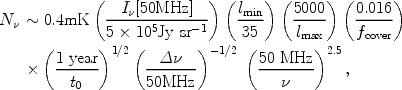(166)

where l_min is the minimum observable l as determined by the field of view of the instruments, l_max is the maximum observable l as determined by the maximum separation of the antennae, f_cover is the fraction of the array area thats is covered by telescopes, t₀ is the observation time and is the frequency range over which the signal can be detected. Note that the assumed sky temperature of 0.7 × 10⁴ K at = 50 MHz (corresponding to z ~ 30) is more than six orders of magnitude larger than the signal. We have already included the fact that several independent maps can be produced by varying the observed frequency. The numbers adopted above are appropriate for the inner core of the LOFAR array (http://www.lofar.org), planned for initial operation in 2006. The predicted signal is ~ 1 mK, and so a year of integration or an increase in the covering fraction are required to observe it with LOFAR. Other experiments whose goal is to detect 21cm fluctuations from the subsequent epoch of reionization at z ~ 6-12 (when ionized bubbles exist and the fluctuations are larger) include the Mileura Wide-Field Array (MWA; http://web.haystack.mit.edu/arrays/MWA/), the Primeval Structure Telescope (PAST; http://arxiv.org/abs/astro-ph/0502029), and in the more distant future the Square Kilometer Array (SKA; http://www.skatelescope.org). The main challenge in detecting the predicted signal from higher redshifts involves its appearance at low frequencies where the sky noise is high. Proposed space-based instruments [194] avoid the terrestrial radio noise and the increasing atmospheric opacity at < 20 MHz (corresponding to z > 70).

Figure 57. Prototype of the tile design for the Mileura Wide-Field Array (MWA) in western Australia, aimed at detecting redshifted 21cm from the epoch of reionization. Each 4m×4m tile contains 16 dipole antennas operating in the frequency range of 80 - 300MHz. Altogether the initial phase of MWA (the so-called "Low-Frequency Demostrator") will include 500 antenna tiles with a total collecting area of 8000 m2 at 150MHz, scattered across a 1.5 km region and providing an angular resolution of a few arcminutes.

The 21cm absorption is replaced by 21cm emission from neutral hydrogen as soon as the intergalactic medium is heated above the CMB temperature by X-ray sources during the epoch of reionization [88]. This occurs long before reionization since the required heating requires only a modest amount of energy, ~ 10^-2 eV[(1 + z) / 30], which is three orders of magnitude smaller than the amount necessary to ionize the Universe. As demonstrated by Chen & Miralda-Escude (2004) [88], heating due the recoil of atoms as they absorb Ly photons [237] is not effective; the Ly color temperature reaches equilibrium with the gas kinetic temperature and suppresses subsequent heating before the level of heating becomes substantial. Once most of the cosmic hydrogen is reionized at z_reion, the 21cm signal is diminished. The optical depth for free-free absorption after reionization, ~ 0.1 [(1 + z_reion) / 20]^5/2, modifies only slightly the expected 21cm anisotropies. Gravitational lensing should modify the power spectrum [287] at high l, but can be separated as in standard CMB studies (see [326] and references therein). The 21cm signal should be simpler to clean as it includes the same lensing foreground in independent maps obtained at different frequencies.

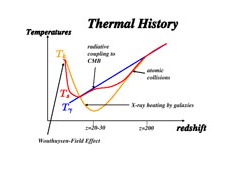Figure 58. Schematic sketch of the evolution of the kinetic temperature (Tk) and spin temperature (Ts) of cosmic hydrogen. Following cosmological recombination at z ~ 103, the gas temperature (orange curve) tracks the CMB temperature (blue line; T (1 + z)) down to z ~ 200 and then declines below it (Tk (1 + z)2) until the first X-ray sources (accreting black holes or exploding supernovae) heat it up well above the CMB temperature. The spin temperature of the 21cm transition (red curve) interpolates between the gas and CMB temperatures. Initially it tracks the gas temperature through collisional coupling; then it tracks the CMB through radiative coupling; and eventually it tracks the gas temperature once again after the production of a cosmic background of UV photons between the Ly and the Lyman-limit frequencies that redshift or cascade into the Ly resonance (through the Wouthuysen-Field effect [Wouthuysen 1952 [388]; Field 1959 [131]]). Parts of the curve are exaggerated for pedagogic purposes. The exact shape depends on astrophysical details about the first galaxies, such as their production of X-ray binaries, supernovae, nuclear accreting black holes, and their generation of relativistic electrons in collisionless shocks which produce UV and X-ray photons through inverse-Compton scattering of CMB photons.

The large number of independent modes probed by the 21cm signal would provide a measure of non-Gaussian deviations to a level of ~ N_{21 cm}^-1/2, constituting a test of the inflationary origin of the primordial inhomogeneities which are expected to possess deviations > 10^-6 [245].

9.2. The Characteristic Observed Size of Ionized Bubbles at the End of Reionization

Figure 59. 21cm imaging of ionized bubbles during the epoch of reionization is analogous to slicing swiss cheese. The technique of slicing at intervals separated by the typical dimension of a bubble is optimal for revealing different pattens in each slice.

The first galaxies to appear in the Universe at redshifts z > 20 created ionized bubbles in the intergalactic medium (IGM) of neutral hydrogen (H I) left over from the Big-Bang. It is thought that the ionized bubbles grew with time, surrounded clusters of dwarf galaxies [67, 143] and eventually overlapped quickly throughout the Universe over a narrow redshift interval near z ~ 6. This event signaled the end of the reionization epoch when the Universe was a billion years old. Measuring the unknown size distribution of the bubbles at their final overlap phase is a focus of forthcoming observational programs aimed at highly redshifted 21cm emission from atomic hydrogen. In this sub-section we follow Wyithe & Loeb (2004) [399] and show that the combined constraints of cosmic variance and causality imply an observed bubble size at the end of the overlap epoch of ~ 10 physical Mpc, and a scatter in the observed redshift of overlap along different lines-of-sight of ~ 0.15. This scatter is consistent with observational constraints from recent spectroscopic data on the farthest known quasars. This result implies that future radio experiments should be tuned to a characteristic angular scale of ~ 0.5° and have a minimum frequency band-width of ~ 8 MHz for an optimal detection of 21cm flux fluctuations near the end of reionization.

During the reionization epoch, the characteristic bubble size (defined here as the spherically averaged mean radius of the H II regions that contain most of the ionized volume [143]) increased with time as smaller bubbles combined until their overlap completed and the diffuse IGM was reionized. However the largest size of isolated bubbles (fully surrounded by H I boundaries) that can be observed is finite, because of the combined phenomena of cosmic variance and causality. Figure 61 presents a schematic illustration of the geometry. There is a surface on the sky corresponding to the time along different lines-of-sight when the diffuse (uncollapsed) IGM was most recently neutral. We refer to it as the Surface of Bubble Overlap (SBO). There are two competing sources for fluctuations in the SBO, each of which is dependent on the characteristic size, R_SBO, of the ionized regions just before the final overlap. First, the finite speed of light implies that 21cm photons observed from different points along the curved boundary of an H II region must have been emitted at different times during the history of the Universe. Second, bubbles on a comoving scale R achieve reionization over a spread of redshifts due to cosmic variance in the initial conditions of the density field smoothed on that scale. The characteristic scale of H II bubbles grows with time, leading to a decline in the spread of their formation redshifts [67] as the cosmic variance is averaged over an increasing spatial volume. However the 21cm light-travel time across a bubble rises concurrently. Suppose a signal 21cm photon which encodes the presence of neutral gas, is emitted from the far edge of the ionizing bubble. If the adjacent region along the line-of-sight has not become ionized by the time this photon reaches the near side of the bubble, then the photon will encounter diffuse neutral gas. Other photons emitted at this lower redshift will therefore also encode the presence of diffuse neutral gas, implying that the first photon was emitted prior to overlap, and not from the SBO. Hence the largest observable scale of H II regions when their overlap completes, corresponds to the first epoch at which the light crossing time becomes larger than the spread in formation times of ionized regions. Only then will the signal photon leaving the far side of the HII region have the lowest redshift of any signal photon along that line-of-sight.

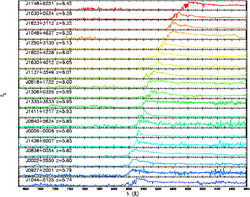Figure 60. Spectra of 19 quasars with redshifts 5.74 < z < 6.42 from the Sloan Digital Sky Survey [128]. For some of the highest-redshift quasars, the spectrum shows no transmitted flux shortward of the Ly wavelength at the quasar redshift (the so-called "Gunn-Peterson trough"), indicating a non-negligible neutral fraction in the IGM (see the analysis of Fan et al. [128] for details).

The observed spectra of some quasars beyond z ~ 6.1 show a Gunn-Peterson trough [163, 127] (Fan et al. 2005 [128]), a blank spectral region at wavelengths shorter than Ly at the quasar redshift, implying the presence of H I in the diffuse IGM. The detection of Gunn-Peterson troughs indicates a rapid change [126, 288, 381] in the neutral content of the IGM at z ~ 6, and hence a rapid change in the intensity of the background ionizing flux. This rapid change implies that overlap, and hence the reionization epoch, concluded near z ~ 6. The most promising observational probe [404, 259] of the reionization epoch is redshifted 21cm emission from intergalactic H I. Future observations using low frequency radio arrays (e.g. LOFAR, MWA, and PAST) will allow a direct determination of the topology and duration of the phase of bubble overlap. In this section we determine the expected angular scale and redshift width of the 21cm fluctuations at the SBO theoretically, and show that this determination is consistent with current observational constraints.

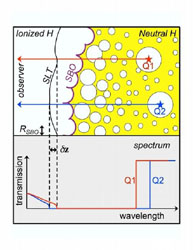Figure 61. The distances to the observed Surface of Bubble Overlap (SBO) and Surface of Ly Transmission (SLT) fluctuate on the sky. The SBO corresponds to the first region of diffuse neutral IGM observed along a random line-of-sight. It fluctuates across a shell with a minimum width dictated by the condition that the light crossing time across the characteristic radius RSBO of ionized bubbles equals the cosmic scatter in their formation times. Thus, causality and cosmic variance determine the characteristic scale of bubbles at the completion of bubble overlap. After some time delay the IGM becomes transparent to Ly photons, resulting in a second surface, the SLT. The upper panel illustrates how the lines-of-sight towards two quasars (Q1 in red and Q2 in blue) intersect the SLT with a redshift difference z. The resulting variation in the observed spectrum of the two quasars is shown in the lower panel. Observationally, the ensemble of redshifts down to which the Gunn-Peterson troughs are seen in the spectra of z > 6.1 quasars is drawn from the probability distribution dP / dzSLT for the redshift at which the IGM started to allow Ly transmission along random lines-of-sight. The observed values of zSLT show a small scatter [127] in the SLT redshift around an average value of < zSLT > 5.95. Some regions of the IGM may have also become transparent to Ly photons prior to overlap, resulting in windows of transmission inside the Gunn-Peterson trough (one such region may have been seen [381] in SDSS J1148+5251). In the existing examples, the portions of the Universe probed by the lower end of the Gunn-Peterson trough are located several hundred comoving Mpc away from the background quasar, and are therefore not correlated with the quasar host galaxy. The distribution dP / dzSLT is also independent of the redshift distribution of the quasars. Moreover, lines-of-sight to these quasars are not causally connected at z ~ 6 and may be considered independent.

We start by quantifying the constraints of causality and cosmic variance. First suppose we have an H II region with a physical radius R / (1 + < z >). For a 21cm photon, the light crossing time of this radius is

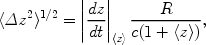(167)

where at the high-redshifts of interest (dz / dt) = -(H_{0 m}^1/2)(1 + z)^5/2. Here, c is the speed of light, H₀ is the present-day Hubble constant, _m is the present day matter density parameter, and < z > is the mean redshift of the SBO. Note that when discussing this crossing time, we are referring to photons used to probe the ionized bubble (e.g. at 21cm), rather than photons involved in the dynamics of the bubble evolution.

Second, overlap would have occurred at different times in different regions of the IGM due to the cosmic scatter in the process of structure formation within finite spatial volumes [67]. Reionization should be completed within a region of comoving radius R when the fraction of mass incorporated into collapsed objects in this region attains a certain critical value, corresponding to a threshold number of ionizing photons emitted per baryon. The ionization state of a region is governed by the enclosed ionizing luminosity, by its over-density, and by dense pockets of neutral gas that are self shielding to ionizing radiation. There is an offset [67] z between the redshift when a region of mean over-density _R achieves this critical collapsed fraction, and the redshift when the Universe achieves the same collapsed fraction on average. This offset may be computed [67] from the expression for the collapsed fraction [52] F_col within a region of over-density _R on a comoving scale R,

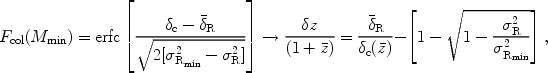(168)

where _c() (1 + ) is the collapse threshold for an over-density at a redshift ; _R and _Rmin are the variances in the power-spectrum linearly extrapolated to z = 0 on comoving scales corresponding to the region of interest and to the minimum galaxy mass M_min, respectively. The offset in the ionization redshift of a region depends on its linear over-density, _R. As a result, the distribution of offsets, and therefore the scatter in the SBO may be obtained directly from the power spectrum of primordial inhomogeneities. As can be seen from equation (168), larger regions have a smaller scatter due to their smaller cosmic variance.

Note that equation (168) is independent of the critical value of the collapsed fraction required for reionization. Moreover, our numerical constraints are very weakly dependent on the minimum galaxy mass, which we choose to have a virial temperature of 10⁴ K corresponding to the cooling threshold of primordial atomic gas. The growth of an H II bubble around a cluster of sources requires that the mean-free-path of ionizing photons be of order the bubble radius or larger. Since ionizing photons can be absorbed by dense pockets of neutral gas inside the H II region, the necessary increase in the mean-free-path with time implies that the critical collapsed fraction required to ionize a region of size R increases as well. This larger collapsed fraction affects the redshift at which the region becomes ionized, but not the scatter in redshifts from place to place which is the focus of this sub-section. Our results are therefore independent of assumptions about unknown quantities such as the star formation efficiency and the escape fraction of ionizing photons from galaxies, as well as unknown processes of feedback in galaxies and clumping of the IGM.

Figure 62 displays the above two fundamental constraints. The causality constraint (Eq. 167) is shown as the blue line, giving a longer crossing time for a larger bubble size. This contrasts with the constraint of cosmic variance (Eq. 168), indicated by the red line, which shows how the scatter in formation times decreases with increasing bubble size. The scatter in the SBO redshift and the corresponding fluctuation scale of the SBO are given by the intersection of these curves. We find that the thickness of the SBO is < z² >^1/2 ~ 0.13, and that the bubbles which form the SBO have a characteristic comoving size of ~ 60 Mpc (equivalent to 8.6 physical Mpc). At z ~ 6 this size corresponds to angular scales of _SBO ~ 0.4 degrees on the sky.

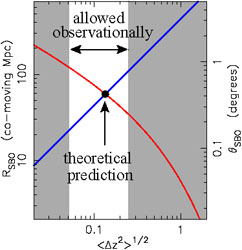Figure 62. Constraints on the scatter in the SBO redshift and the characteristic size of isolated bubbles at the final overlap stage, RSBO (see Fig. 1). The characteristic size of H II regions grows with time. The SBO is observed for the bubble scale at which the light crossing time (blue line) first becomes smaller than the cosmic scatter in bubble formation times (red line). At z ~ 6, the implied scale RSBO ~ 60 comoving Mpc (or ~ 8.6 physical Mpc), corresponds to a characteristic angular radius of SLT ~ 0.4 degrees on the sky. After bubble overlap, the ionizing intensity grows to a level at which the IGM becomes transparent to Ly photons. The collapsed fraction required for Ly transmission within a region of a certain size will be larger than required for its ionization. However, the scatter in equation (168) is not sensitive to the collapsed fraction, and so may be used for both the SBO and SLT. The scatter in the SLT is smaller than the cosmic scatter in the structure formation time on the scale of the mean-free-path for ionizing photons. This mean-free-path must be longer than RSBO ~ 60 Mpc, an inference which is supported by analysis of the Ly forest at z ~ 4 where the mean-free-path is estimated [257] to be ~ 120 comoving Mpc at the Lyman limit (and longer at higher frequencies). If it is dominated by cosmic variance, then the scatter in the SLT redshift provides a lower limit to the SBO scatter. The three known quasars at z > 6.1 have Ly transmission redshifts of [381, 127] zSLT = 5.9, 5.95 and 5.98, implying that the scatter in the SBO must be > 0.05 (this scatter may become better known from follow-up spectroscopy of Gamma Ray Burst afterglows at z>6 that might be discovered by the SWIFT satellite[26, 61]). The observed scatter in the SLT redshift is somewhat smaller than the predicted SBO scatter, confirming the expectation that cosmic variance is smaller at the SLT. The scatter in the SBO redshift must also be < 0.25 because the lines-of-sight to the two highest redshift quasars have a redshift of Ly transparency at z ~ 6, but a neutral fraction that is known from the proximity effect [396] to be substantial at z > 6.2-6.3. The excluded regions of scatter for the SBO are shown in gray.

A scatter of ~ 0.15 in the SBO is somewhat larger than the value extracted from existing numerical simulations [152, 402]. The difference is most likely due to the limited size of the simulated volumes; while the simulations appropriately describe the reionization process within limited regions of the Universe, they are not sufficiently large to describe the global properties of the overlap phase [67]. The scales over which cosmological radiative transfer has been simulated are smaller than the characteristic extent of the SBO, which we find to be R_SBO ~ 70 comoving Mpc.

We can constrain the scatter in the SBO redshift observationally using the spectra of the highest redshift quasars. Since only a trace amount of neutral hydrogen is needed to absorb Ly photons, the time where the IGM becomes Ly transparent need not coincide with bubble overlap. Following overlap the IGM was exposed to ionizing sources in all directions and the ionizing intensity rose rapidly. After some time the ionizing background flux was sufficiently high that the H I fraction fell to a level at which the IGM allowed transmission of resonant Ly photons. This is shown schematically in Figure 61. The lower wavelength limit of the Gunn-Peterson trough corresponds to the Ly wavelength at the redshift when the IGM started to allow transmission of Ly photons along that particular line-of-sight. In addition to the SBO we therefore also define the Surface of Ly Transmission (hereafter SLT) as the redshift along different lines-of-sight when the diffuse IGM became transparent to Ly photons.

The scatter in the SLT redshift is an observable which we would like to compare with the scatter in the SBO redshift. The variance of the density field on large scales results in the biased clustering of sources [67]. H II regions grow in size around these clusters of sources. In order for the ionizing photons produced by a cluster to advance the walls of the ionized bubble around it, the mean-free-path of these photons must be of order the bubble size or larger. After bubble overlap, the ionizing intensity at any point grows until the ionizing photons have time to travel across the scale of the new mean-free-path, which represents the horizon out to which ionizing sources are visible. Since the mean-free-path is larger than R_SBO, the ionizing intensity at the SLT averages the cosmic scatter over a larger volume than at the SBO. This constraint implies that the cosmic variance in the SLT redshift must be smaller than the scatter in the SBO redshift. However, it is possible that opacity from small-scale structure contributes additional scatter to the SLT redshift.

If cosmic variance dominates the observed scatter in the SLT redshift, then based on the spectra of the three z > 6.1 quasars [127, 381] we would expect the scatter in the SBO redshift to satisfy < z² >_obs^1/2 > 0.05. In addition, analysis of the proximity effect for the size of the H II regions around the two highest redshift quasars [396, 251] implies a neutral fraction that is of order unity (i.e. pre-overlap) at z ~ 6.2-6.3, while the transmission of Ly photons at z < 6 implies that overlap must have completed by that time. This restricts the scatter in the SBO to be < z² >_obs^1/2 < 0.25. The constraints on values for the scatter in the SBO redshift are shaded gray in Figure 62. It is reassuring that the theoretical prediction for the SBO scatter of < z² >_obs^1/2 ~ 0.15, with a characteristic scale of ~ 70 comoving Mpc, is bounded by these constraints.

The possible presence of a significantly neutral IGM just beyond the redshift of overlap [396, 251] is encouraging for upcoming 21cm studies of the reionization epoch as it results in emission near an observed frequency of 200 MHz where the signal is most readily detectable. Future observations of redshifted 21cm line emission at 6 < z < 6.5 with instruments such as LOFAR, MWA, and PAST, will be able to map the three-dimensional distribution of HI at the end of reionization. The intergalactic H II regions will imprint a 'knee' in the power-spectrum of the 21cm anisotropies on a characteristic angular scale corresponding to a typical isolated H II region [404]. Our results suggest that this characteristic angular scale is large at the end of reionization, _SBO ~ 0.5 degrees, motivating the construction of compact low frequency arrays. An SBO thickness of < z² >^1/2 ~ 0.15 suggests a minimum frequency band-width of ~ 8 MHz for experiments aiming to detect anisotropies in 21cm emission just prior to overlap. These results will help guide the design of the next generation of low-frequency radio observatories in the search for 21cm emission at the end of the reionization epoch.

The full size distribution of ionized bubbles has to be calculated from a numerical cosmological simulation that includes gas dynamics and radiative transfer. The simulation box needs to be sufficiently large for it to sample an unbiased volume of the Universe with little cosmic variance, but at the same time one must resolve the scale of individual dwarf galaxies which provide (as well as consume) ionizing photons (see discussion at the last section of this review). Until a reliable simulation of this magnitude exists, one must adopt an approximate analytic approach to estimate the bubble size distribution. Below we describe an example for such a method, developed by Furlanetto, Zaldarriaga, & Hernquist (2004) [143].

The criterion for a region to be ionized is that galaxies inside of it produce a sufficient number of ionizing photons per baryon. This condition can be translated to the requirement that the collapsed fraction of mass in halos above some threshold mass M_min will exceed some threshold, namely F_col > ^-1. The minimum halo mass most likely corresponds to a virial temperature of 10⁴ K relating to the threshold for atomic cooling (assuming that molecular hydrogen cooling is suppressed by the UV background in the Lyman-Werner band). We would like to find the largest region around every point that satisfies the above condition on the collapse fraction and then calculate the abundance of ionized regions of this size. Different regions have different values of F_col because their mean density is different. In the extended Press-Schechter model (Bond et al. 1991 [52]; Lacey & Cole 1993 [212]), the collapse fraction in a region of mean overdensity _M is

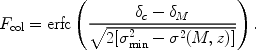(169)

where ²(M, z) is the variance of density fluctuations on mass scale M, _min^{2 2}(M_min, z), and _c is the collapse threshold. This equation can be used to derive the condition on the mean overdensity within a region of mass M in order for it to be ionized,

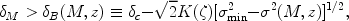(170)

where K() = erfc^-1(1 - ^-1). Furlanetto et al. [143] showed how to construct the mass function of ionized regions from _b in analogy with the halo mass function (Press & Schechter 1974 [291]; Bond et al. 1991 [52]). The barrier in equation (170) is well approximated by a linear dependence on ²,

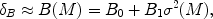(171)

in which case the mass function has an analytic solution (Sheth 1998 [332]),

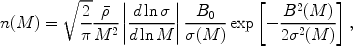(172)

where is the mean mass density. This solution provides the comoving number density of ionized bubbles with mass in the range of (M, M + dM). The main difference of this result from the Press-Schechter mass function is that the barrier in this case becomes more difficult to cross on smaller scales because _B is a decreasing function of mass M. This gives bubbles a characteristic size. The size evolves with redshift in a way that depends only on and M_min.

One limitation of the above analytic model is that it ignores the non-local influence of sources on distant regions (such as voids) as well as the possible shadowing effect of intervening gas. Radiative transfer effects in the real Universe are inherently three-dimensional and cannot be fully captured by spherical averages as done in this model. Moreover, the value of M_min is expected to increase in regions that were already ionized, complicating the expectation of whether they will remain ionized later. The history of reionization could be complicated and non monotonic in individual regions, as described by Furlanetto & Loeb (2005) [144]. Finally, the above analytic formalism does not take the light propagation delay into account as we have done above in estimating the characteristic bubble size at the end of reionization. Hence this formalism describes the observed bubbles only as long as the characteristic bubble size is sufficiently small, so that the light propagation delay can be neglected compared to cosmic variance. The general effect of the light propagation delay on the power-spectrum of 21cm fluctuations was quantified by Barkana & Loeb (2005) [29].

9.3. Separating the "Physics" from the "Astrophysics" of the Reionization Epoch with 21cm Fluctuations

The 21cm signal can be seen from epochs during which the cosmic gas was largely neutral and deviated from thermal equilibrium with the cosmic microwave background (CMB). The signal vanished at redshifts z > 200, when the residual fraction of free electrons after cosmological recombination kept the gas kinetic temperature, T_k, close to the CMB temperature, T. But during 200 > z > 30 the gas cooled adiabatically and atomic collisions kept the spin temperature of the hyperfine level population below T, so that the gas appeared in absorption [323, 226]. As the Hubble expansion continued to rarefy the gas, radiative coupling of T_s to T began to dominate and the 21cm signal faded. When the first galaxies formed, the UV photons they produced between the Ly and Lyman limit wavelengths propagated freely through the Universe, redshifted into the Ly resonance, and coupled T_s and T_k once again through the Wouthuysen-Field [388, 131] effect by which the two hyperfine states are mixed through the absorption and re-emission of a Ly photon [237, 96]. Emission above the Lyman limit by the same galaxies initiated the process of reionization by creating ionized bubbles in the neutral cosmic gas, while X-ray photons propagated farther and heated T_k above T throughout the Universe. Once T_s grew larger than T, the gas appeared in 21cm emission. The ionized bubbles imprinted a knee in the power spectrum of 21cm fluctuations [404], which traced the H I topology until the process of reionization was completed [143].

The various effects that determine the 21cm fluctuations can be separated into two classes. The density power spectrum probes basic cosmological parameters and inflationary initial conditions, and can be calculated exactly in linear theory. However, the radiation from galaxies, both Ly radiation and ionizing photons, involves the complex, non-linear physics of galaxy formation and star formation. If only the sum of all fluctuations could be measured, then it would be difficult to extract the separate sources, and in particular, the extraction of the power spectrum would be subject to systematic errors involving the properties of galaxies. Barkana & Loeb (2005) [28] showed that the unique three-dimensional properties of 21cm measurements permit a separation of these distinct effects. Thus, 21cm fluctuations can probe astrophysical (radiative) sources associated with the first galaxies, while at the same time separately probing the physical (inflationary) initial conditions of the Universe. In order to affect this separation most easily, it is necessary to measure the three-dimensional power spectrum of 21cm fluctuations. The discussion in this section follows Barkana & Loeb (2005) [28].

Spin temperature history

As long as the spin-temperature T_s is smaller than the CMB temperature T = 2.725 (1 + z) K, hydrogen atoms absorb the CMB, whereas if T_s > T they emit excess flux. In general, the resonant 21cm interaction changes the brightness temperature of the CMB by [323, 237] T_b = ( T_s - T) / (1 + z), where the optical depth at a wavelength = 21cm is

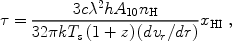(173)

where n_H is the number density of hydrogen, A₁₀ = 2.85 × 10^-15 s^-1 is the spontaneous emission coefficient, x_HI is the neutral hydrogen fraction, and dv_r / dr is the gradient of the radial velocity along the line of sight with v_r being the physical radial velocity and r the comoving distance; on average dv_r / dr = H(z) / (1 + z) where H is the Hubble parameter. The velocity gradient term arises because it dictates the path length over which a 21cm photon resonates with atoms before it is shifted out of resonance by the Doppler effect [341].

For the concordance set of cosmological parameters [348], the mean brightness temperature on the sky at redshift z is

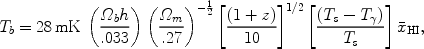(174)

where _HI is the mean neutral fraction of hydrogen. The spin temperature itself is coupled to T_k through the spin-flip transition, which can be excited by collisions or by the absorption of Ly photons. As a result, the combination that appears in T_b becomes [131] (T_s - T) / T_s = [x_tot / (1 + x_tot)] (1 - T / T_k ), where x_tot = x + x_c is the sum of the radiative and collisional threshold parameters. These parameters are x = 4 P T_* / 27 A₁₀ T and x_c = 4 _1-0(T_k) n_H T_* / 3A₁₀ T, where P is the Ly scattering rate which is proportional to the Ly intensity, and _1-0 is tabulated as a function of T_k [11, 406]. The coupling of the spin temperature to the gas temperature becomes substantial when x_tot > 1.

Brightness temperature fluctuations

Although the mean 21cm emission or absorption is difficult to measure due to bright foregrounds, the unique character of the fluctuations in T_b allows for a much easier extraction of the signal [154, 404, 259, 260, 314]. We adopt the notation _A for the fractional fluctuation in quantity A (with a lone denoting density perturbations). In general, the fluctuations in T_b can be sourced by fluctuations in gas density (), Ly flux (through _x) neutral fraction (_xHI), radial velocity gradient (_drvr), and temperature, so we find

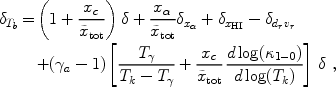(175)

where the adiabatic index is _a = 1 + (_Tk / ), and we define _tot (1 + x_tot) x_tot. Taking the Fourier transform, we obtain the power spectrum of each quantity; e.g., the total power spectrum P_Tb is defined by

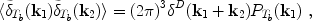(176)

where _Tb (k) is the Fourier transform of _Tb, k is the comoving wavevector, ^D is the Dirac delta function, and < ... > denotes an ensemble average. In this analysis, we consider scales much bigger than the characteristic bubble size and the early phase of reionization (when 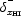<< 1), so that the fluctuations _xHI are also much smaller than unity. For a more general treatment, see McQuinn et al. (2005) [250].

The separation of powers

The fluctuation _Tb consists of a number of isotropic sources of fluctuations plus the peculiar velocity term -_drvr. Its Fourier transform is simply proportional to that of the density field [191, 41],

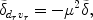(177)

where µ = cos _k in terms of the angle _k of k with respect to the line of sight. The µ² dependence in this equation results from taking the radial (i.e., line-of-sight) component ( µ) of the peculiar velocity, and then the radial component ( µ) of its gradient. Intuitively, a high-density region possesses a velocity infall towards the density peak, implying that a photon must travel further from the peak in order to reach a fixed relative redshift, compared with the case of pure Hubble expansion. Thus the optical depth is always increased by this effect in regions with > 0. This phenomenon is most properly termed velocity compression.

We therefore write the fluctuation in Fourier space as

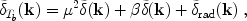(178)

where we have defined a coefficient by collecting all terms in Eq. (175), and have also combined the terms that depend on the radiation fields of Ly photons and ionizing photons, respectively. We assume that these radiation fields produce isotropic power spectra, since the physical processes that determine them have no preferred direction in space. The total power spectrum is

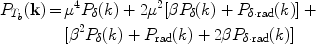(179)

where we have defined the power spectrum P _{. rad} as the Fourier transform of the cross-correlation function,

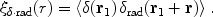(180)

We note that a similar anisotropy in the power spectrum has been previously derived in a different context, i.e., where the use of galaxy redshifts to estimate distances changes the apparent line-of-sight density of galaxies in redshift surveys [191, 219, 178, 133]. However, galaxies are intrinsically complex tracers of the underlying density field, and in that case there is no analog to the method that we demonstrate below for separating in 21cm fluctuations the effect of initial conditions from that of later astrophysical processes.

The velocity gradient term has also been examined for its global effect on the sky-averaged power and on radio visibilities [366, 41]. The other sources of 21cm perturbations are isotropic and would produce a power spectrum P_Tb(k) that could be measured by averaging the power over spherical shells in k space. In the simple case where = 1 and only the density and velocity terms contribute, the velocity term increases the total power by a factor o < (1 + µ²)² > = 1.87 in the spherical average. However, instead of averaging the signal, we can use the angular structure of the power spectrum to greatly increase the discriminatory power of 21cm observations. We may break up each spherical shell in k space into rings of constant µ and construct the observed P_Tb(k,µ). Considering Eq. (179) as a polynomial in µ, i.e., µ⁴ P_µ⁴ + µ² P_µ² + P_µ⁰, we see that the power at just three values of µ is required in order to separate out the coefficients of 1, µ², and µ⁴ for each k.

If the velocity compression were not present, then only the µ-independent term (times Tb2) would have been observed, and its separation into the five components (Tb, , and three power spectra) would have been difficult and subject to degeneracies. Once the power has been separated into three parts, however, the µ4 coefficient can be used to measure the density power spectrum directly, with no interference from any other source of fluctuations. Since the overall amplitude of the power spectrum, and its scaling with redshift, are well determined from the combination of the CMB temperature fluctuations and galaxy surveys, the amplitude of Pµ4 directly determines the mean brightness temperature Tb on the sky, which measures a combination of Ts and HI at the observed redshift. McQuinn et al. (2005) [250] analysed in detail the parameters that can be constrained by upcoming 21cm experiments in concert with future CMB experiments such as Planck (http://www.rssd.esa.int/index.php?project=PLANCK). Once P(k) has been determined, the coefficients of the µ2 term and the µ-independent term must be used to determine the remaining unknowns, , P . rad(k), and Prad(k). Since the coefficient is independent of k, determining it and thus breaking the last remaining degeneracy requires only a weak additional assumption on the behavior of the power spectra, such as their asymptotic behavior at large or small scales. If the measurements cover Nk values of wavenumber k, then one wishes to determine 2 Nk + 1 quantities based on 2 Nk measurements, which should not cause significant degeneracies when Nk >> 1. Even without knowing , one can probe whether some sources of Prad(k) are uncorrelated with ; the quantity Pun-(k) Pµ0 - Pµ22 / (4 Pµ4) equals Prad - P . rad2 / P, which receives no contribution from any source that is a linear functional of the density distribution (see the next subsection for an example).

Specific epochs

At z ~ 35, collisions are effective due to the high gas density, so one can measure the density power spectrum [226] and the redshift evolution of n_HI, T, and T_k. At z < 35, collisions become ineffective but the first stars produce a cosmic background of Ly photons (i.e. photons that redshift into the Ly resonance) that couples T_s to T_k. During the period of initial Ly coupling, fluctuations in the Ly flux translate into fluctuations in the 21cm brightness [30]. This signal can be observed from z ~ 25 until the Ly coupling is completed (i.e., x_tot >> 1) at z ~ 15. At a given redshift, each atom sees Ly photons that were originally emitted at earlier times at rest-frame wavelengths between Ly and the Lyman limit. Distant sources are time retarded, and since there are fewer galaxies in the distant, earlier Universe, each atom sees sources only out to an apparent source horizon of ~ 100 comoving Mpc at z ~ 20. A significant portion of the flux comes from nearby sources, because of the 1 / r² decline of flux with distance, and since higher Lyman series photons, which are degraded to Ly photons through scattering, can only be seen from a small redshift interval that corresponds to the wavelength interval between two consecutive atomic levels.

There are two separate sources of fluctuations in the Ly flux [30]. The first is density inhomogeneities. Since gravitational instability proceeds faster in overdense regions, the biased distribution of rare galactic halos fluctuates much more than the global dark matter density. When the number of sources seen by each atom is relatively small, Poisson fluctuations provide a second source of fluctuations. Unlike typical Poisson noise, these fluctuations are correlated between gas elements at different places, since two nearby elements see many of the same sources. Assuming a scale-invariant spectrum of primordial density fluctuations, and that x = 1 is produced at z = 20 by galaxies in dark matter halos where the gas cools efficiently via atomic cooling, Figure 63 shows the predicted observable power spectra. The figure suggests that can be measured from the ratio P_µ² / P_µ⁴ at k > 1 Mpc^-1, allowing the density-induced fluctuations in flux to be extracted from P_µ², while only the Poisson fluctuations contribute to P_un-. Each of these components probes the number density of galaxies through its magnitude, and the distribution of source distances through its shape. Measurements at k > 100 Mpc^-1 can independently probe T_k because of the smoothing effects of the gas pressure and the thermal width of the 21cm line.

Figure 63. Observable power spectra during the period of initial Ly coupling. Upper panel: Assumes adiabatic cooling. Lower panel: Assumes pre-heating to 500 K by X-ray sources. Shown are Pµ4 = P (solid curves), Pµ2 (short-dashed curves), and Pun- (long-dashed curves), as well as for comparison 2 P (dotted curves).

Full-sky observations must normally be analyzed with an angular and radial transform [143, 314, 41], rather than a Fourier transform which is simpler and yields more directly the underlying 3D power spectrum [259, 260]. The 21cm brightness fluctuations at a given redshift - corresponding to a comoving distance r₀ from the observer - can be expanded in spherical harmonics with expansion coefficients a_lm(), where the angular power spectrum is

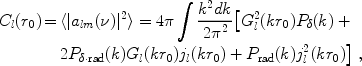(181)

with G_l(x) J_l(x) + ( - 1) j_l(x) and J_l(x) being a linear combination of spherical Bessel functions [41].

In an angular transform on the sky, an angle of radians translates to a spherical multipole l ~ 3.5 / . For measurements on a screen at a comoving distance r₀, a multipole l normally measures 3D power on a scale of k^-1 ~ r₀ ~ 35/l Gpc for l >> 1, since r₀ ~ 10 Gpc at z > 10. This estimate fails at l < 100, however, when we consider the sources of 21cm fluctuations. The angular projection implied in C_l involves a weighted average (Eq. 181) that favors large scales when l is small, but density fluctuations possess little large-scale power, and the C_l are dominated by power around the peak of k P(k), at a few tens of comoving Mpc.

Figure 64. Effect of large-scale power on the angular power spectrum of 21cm anisotropies on the sky. This example shows the power from density fluctuations and velocity compression, assuming a warm IGM at z = 12 with Ts = Tk >> T. Shown is the % change in Cl if we were to cut off the power spectrum above 1 / k of 200, 180, 160, 140, 120, and 100 Mpc (top to bottom). Also shown for comparison is the cosmic variance for averaging in bands of l ~ l (dashed lines).

Figure 64 shows that for density and velocity fluctuations, even the l = 1 multipole is affected by power at k^-1 > 200 Mpc only at the 2% level. Due to the small number of large angular modes available on the sky, the expectation value of C_l cannot be measured precisely at small l. Figure 64 shows that this precludes new information from being obtained on scales k^-1 > 130 Mpc using angular structure at any given redshift. Fluctuations on such scales may be measurable using a range of redshifts, but the required z > 1 at z ~ 10 implies significant difficulties with foreground subtraction and with the need to account for time evolution.