5. AFTERGLOW RADIATION MODELS

5.1. The standard model

The external shock starts to develop as soon as the ejecta expands into the external medium. As the ejecta plows ahead, it sweeps up an increasing amount of external matter, and the bolometric luminosity of the shock increases as L t² (equating in the contact discontinuity frame the kinetic flux L / 4 r^{2 2} to the external ram pressure _ext ² while ~ ₀ = ~ constant, r 2 ² ct t [403]). The luminosity peaks after has dropped to about half its initial value, at a radius r_dec at an observer time t_dec given by equations (15,16). Thereafter, as more matter is swept up, the bulk Lorentz factor and the radius vary as [403, 356] as

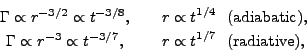(25)

or in general r^-g t^-g/(1+2g), r t^1/(1+2g) with g = (3,3/2) for the radiative (adiabatic) regime. In the adiabatic case the radiative cooling time, e.g. synchrotron, is longer than the observer-frame dynamical time t ~ r / 2 c ², so the energy is approximately conserved E = (4 / 3) r³ n₀ m_p c^{2 2} ~ constant (c.f. equation [15]), while in the radiative case the cooling time is shorter than the dynamic time and momentum is conserved (as in the snow-plow phase of supernova remnants), n_o r³ ~ constant. Thus, after the external shock luminosity peaks, one expects the bolometric luminosity to decay as L t^-1 in the adiabatic regime [403] or steeper in the radiative regime, in a gradual fading. The observed time-radius relation is more generally t ~ r / K c ², where K = 2 in the constant regime, and K = 4 in the self-similar (BM) regime [497, 433].

The spectrum of radiation is likely to be due to synchrotron radiation, whose peak frequency in the observer frame is _m B' _e², and both the comoving field B' and electron Lorentz factor _e are likely to be proportional to [301]. This implies that as decreases, so will _m, and the radiation will move to longer wavelengths. Consequences of this are the expectation that the burst would leave a radio remnant [347] after some weeks, and before that an optical [218] transient. The observation of linear polarization at the few percent level observed in a number of optical or IR afterglows (e.g. [471]) supports the paradigm of synchrotron emission as the dominant emission mechanism in the afterglow.

The first self-consistent afterglow calculations [305] took into account both the dynamical evolution and its interplay with the relativistic particle acceleration and a specific relativistically beamed radiation mechanism resulted in quantitative predictions for the entire spectral evolution, going through the X-ray, optical and radio range. For a spherical fireball advancing into an approximately smooth external environment, the bulk Lorentz factor decreases as in inverse power of the time (asymptotically t^-3/8 in the adiabatic limit), and the accelerated electron minimum random Lorentz factor and the turbulent magnetic field also decrease as inverse power laws in time. The synchrotron peak energy corresponding to the time-dependent minimum Lorentz factor and magnetic field then moves to softer energies as t^-3/2. These can be generalized in a straightforward manner when in the radiative regime, or in presence of density gradients, etc.. The radio spectrum is initially expected to be self-absorbed, and becomes optically thin after ~ hours. For times beyond ~ 10 minutes, the dominant radiation is from the forward shock, for which the flux at a given frequency and the synchrotron peak frequency decay as [305]

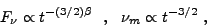(26)

as long as the expansion is relativistic. This is referred to as the "standard" (adiabatic) model, where g = 3/2 in r^-g and = d log F / d log is the photon spectral energy flux slope. More generally [307] the relativistic forward shock flux and frequency peak are given by

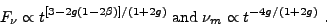(27)

where g = (3/2,3) for the adiabatic (radiative) regime. The transition to the non-relativistic expansion regime has been discussed, e.g. by [515, 81, 273]. A reverse shock component is also expected [302, 305, 441, 307], with high initial optical brightness but much faster decay rate than the forward shock, see Section 5.2). Remarkably, the simple "standard" model where reverse shock effects are ignored is a good approximation for modeling observations starting a few hours after the trigger, as during 1997-1998.

The afterglow spectrum at a given instant of time depends on the flux observed at different frequencies from electrons with (comoving) energy _e m_c c² and bulk Lorentz factor , whose observed peak frequency is = _e² (eB' / 2 m_e c). Three critical frequencies are defined by the three characteristic electron energies. These are _m (the "peak" or injection frequency corresponding to _m), _c (the cooling frequency), and _m (the maximum synchrotron frequency). There is one more frequency, _a, corresponding to the synchrotron self-absorption at lower frequencies. For a given behavior of with r or t (e.g. adiabatic, r^-3/2) and values of the isotropic equivalent kinetic energy of the explosion, of the electron index (e.g. p = 2.2) and the efficiency factors _e, _e, _b, one can obtain the time dependence of the characteristic observer-frame frequencies, including also a cosmological redshift factor z [525]

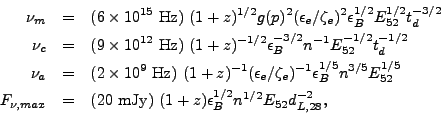(28) (29) (30) (31)

where t_d = (t / day) and g(p) = (p - 2) / (p - 1). The final GRB afterglow synchrotron spectrum is a four-segment broken power law [440, 308, 175, 525] separated by the typical frequencies _a, _m, and _c (Figure 7). Depending on the order between _m and _c, there are two types of spectra [440]. For _m < _c, called the "slow cooling case", the spectrum is

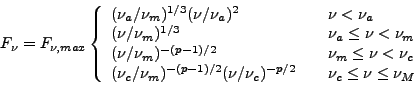(32)

For _m > _c, called the "fast cooling case", the spectrum is

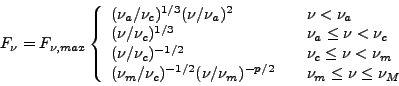(33)

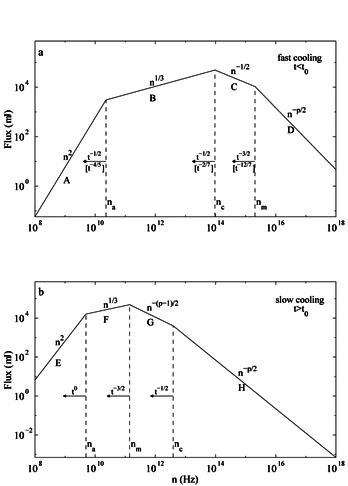Figure 7. Fast cooling and slow cooling synchrotron spectra [440]

A useful tabulation of the temporal indices and spectral indices is given in Table 1 of [525], corresponding to the various forward shock spectral regimes of equations (32),(33), for a homogeneous or a wind external medium. In the above, the normalization F_,max is obtained by multiplying the total number of radiating electrons 4 r³ n₁ / 3 by the peak flux from a single electron [440], which is only a function of B and is independent of the energy (_e) of the electron [440, 510]. There are more complicated regimes for various cases of self-absorption [172], e.g. there can also be an intermediate fast cooling optically thick power law segment of the synchrotron spectrum where F ^11/8.

The predictions of the fireball shock afterglow model [305] were made in advance of the first X-ray detections by Beppo-SAX [74] allowing subsequent follow-ups [472, 295, 133] over different wavelengths, which showed a good agreement with the standard model, e.g. [483, 515, 463, 495, 496, 400]. The comparison of increasingly sophisticated versions of this theoretical model (e.g. [440, 510, 376, 97, 98, 175]) against an increasingly detailed array of observations (e.g. as summarized in [471]) has provided confirmation of this generic fireball shock model of GRB afterglows.

A snapshot spectrum of the standard model at any given time consists generally of three or four segment power law with two or three breaks, such as those shown in Figure 7. (More rarely, a five segment power law spectrum may also be expected [172]). The observations (e.g. [471]) are compatible with an electron spectral index p ~ 2.2 - 2.5, which is typical of shock acceleration, e.g. [495, 440, 510], etc. As the remnant expands the photon spectrum moves to lower frequencies, and the flux in a given band decays as a power law in time, whose index can change as the characteristic frequencies move through it. Snapshot spectra have been deduced by extrapolating measurements at different wavelengths and times, and assuming spherical symmetry and using the model time dependences [496, 510], fits were obtained for the different physical parameters of the burst and environment, e.g. the total energy E, the magnetic and electron-proton coupling parameters _b and _e and the external density n_o. These lead to typical values n_o ~ 10^-2 - 10 cm^-3, _B ~ 10^-2, _e ~ 0.1-0.5 and E ~ 10⁵² - 10⁵⁴ ergs (if spherical; but see Section 5.5).

5.2. Prompt Flashes and Reverse Shocks

An interesting development was the observation [4] of a prompt and extremely bright (m_v ~ 9) optical flash in the burst GRB 990123, the first data point for which was at 15 seconds after the GRB started (while the gamma-rays were still going on). This observation was followed by a small number of other prompt optical flashes, generally not as bright. A prompt multi-wavelength flash, contemporaneous with the -ray emission and reaching such optical magnitude levels is an expected consequence of the reverse component of external shocks [302, 305, 441, 307]. Generally the reverse shock can expected to be mildly relativistic (thin shell case; see, however, below). In this case the thermal Lorentz factor of the reverse electrons is roughly _e^r ~ _e m_p / m_e (whereas in the forward shock, the thermal Lorentz factor of the electrons is _e^f ~ _e m_p / m_e. In this case the reverse electrons radiate much softer radiation than the forward shock electrons. This follows also from the fact that the reverse shock has a similar total energy as the forward shock, but consists of times more electrons, hence the energy per electron is 1 / times smaller [305]. In general, since the pressure (and hence the magnetic energy density) is the same in the forward and reverse shocked regions, one has the following relations between forward and reverse shock radiation properties [437]: 1) The peak flux of the reverse shock, at any time, is larger by a factor of than that of the forward shock, F_,max^r = F_,max ^f; 2) The typical frequency of the minimal electron in the reverse shock is smaller by a factor of ², _m^r = _m^f / ²; 3) The cooling frequency of the reverse and forward shock are equal, _c^r = _c^f = _c (under the assumption that _b is the same in the forward and reverse shocked gas; this might not be true if the ejecta carries a significant magnetic field from the source); 4) Generally (also in refreshed shocks) _a^r,f < _m^r,f and _a^r,f < _c. The self-absorption frequency of the reverse shock is larger than that of the forward shock. The characteristic frequencies and flux temporal slopes for a standard afterglow are given by the case (r) with s = 0 in Table 1 below.

The prompt optical flashes, starting with GRB 990123, have been generally interpreted [441, 307, 327] as the radiation from a reverse (external) shock, although a prompt optical flash could be expected from either an internal shock or the reverse part of the external shock, or both [305]. The decay rate of the optical flux from reverse shocks is much faster (and that of internal shocks is faster still) than that of forward shocks, so the emission of the latter dominate after tens of minutes [169]. Such bright prompt flashes, however, appear to be relatively rare. Other early optical flashes, e.g. in GRB 021004, GRB 021211, GRB 041219a, GRB 050904 are also consistent with the reverse shock interpretation [233, 521, 128, 129, 506, 112, 507]. After the launch of Swift, new prompt optical observations with robotic telescopes have greatly added to the phenomenology of prompt flashes (see Section 3).

5.3. Dependence on external density, injection variability and anisotropy

If the external medium is inhomogeneous, e.g. n_ext r^-k, the energy conservation condition is ² r^3-k ~ constant, so t^{1/(4 - k)}, r t^{-(3-k)/(8-2k)}, which changes the temporal decay rates [308]. This might occur if the external medium is a stellar wind from the evolved progenitor star of a long burst, e.g. n_ext r^-2, such light curves fitting some bursts better with this hypothesis [66, 267].

Another departure from a simple injection approximation is one where E₀ (or L₀) and ₀ are not a simple a delta function or top hat functions. An example is if the mass and energy injected during the burst duration t_grb (say tens of seconds) obeys M(> ) ^-s, E(> ) ^1-s, i.e. more energy emitted with lower Lorentz factors at later times, but still shorter than the gamma-ray pulse duration [405, 437]. The ejecta dynamics becomes

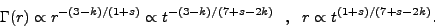(34)

This can drastically change the temporal decay rate, extending the afterglow lifetime in the relativistic regime. If can provide an explanation for shallower decay rates, if the progressively slower ejecta arrives continuously, re-energizing the external shocks ("refreshed" shocks) on timescales comparable to the afterglow time scale [405, 247, 82, 437]. While observational motivations for this were present already in the Beppo-SAX era, as discussed in the above references, this mechanism has been invoked more recently in order to explain the Swift prompt X-ray afterglow shallow decays (see Section 6.2). When the distribution of is discontinuous, it can also explain a sudden increase in the flux, leading to bumps in the light curve. After the onset, the non-standard decay rates for the forward and reverse shock are tabulated for different cases [437] in Table 1.

Table 1. Temporal exponents of the peak frequency _m, the maximum flux F_m, the cooling frequency _c and the flux in a given bandwidth F, for the forward (f) and reverse (r) shocks, calculated both in the adiabatic regime _m < < _c (F F_m(_m / ) t^{- -}, where = (p - 1) / 2), and in the cooling regime _c < _m < (F (_c / _m)^1/2 (_m / ) t^{- -} where = p / 2). For s = 1 this gives the usual (i.e. without "refreshment") forward and reverse shock behavior [437, 405].

	m	Fm	c	F: m < < c	F: > max(c, m)
f	-[24-7k+sk] / [2(7+s-2k)]	[6s-6+k-3sk] / [2(7+s-2k)]	-[4+4s-3k-3sk] / [2(7+s-2k)]	-[6-6s-k+3sk+(24-7k+sk)] / [2(7+s-2k)]	-[-4-4s+k+sk+(24-7k+sk)] / [2(7+s-2k)]
r	-[12-3k+sk] / [2(7+s-2k)]	[6s-12+3k-3sk] / [2(7+s-2k)]	-[4+4s-3k-3sk] / [2(7+s-2k)]	-[12-6s-3k+3sk+(12-3k+sk)] / [2(7+s-2k)]	-[8-4s-3k+sk+(12-3k+sk)] / [2(7+s-2k)]

Other types of non-standard decay can occur if the outflow has a transverse dependent gradient in the energy or Lorentz factor, e.g. as some power law E ^-a, ^-b [308]. Expressions for the temporal decay index (, s, d, a, b,..) in F t are given by [308, 437], which now depend also on s, d, a, b, etc. (and not just on as in the standard relation of equ. (26). The result is that the decay can be flatter (or steeper, depending on s, d, etc)) than the simple standard = (3/2). Such non-uniform outflows have been considered more recently in the context of jet breaks based on structured jets (Section 5.5).

Evidence for departures from the simple standard model was present even before the new Swift observations, by e.g. sharp rises or humps in the light curves followed by a renewed decay, as in GRB 970508 [363, 378], or shallower than usual light curve decays. Time-dependent model fits [359] to the X-ray, optical and radio light curves of GRB 970228 and GRB 970508 indicated that in order to explain the humps, a non-uniform injection or an anisotropic outflow is required. Another example is the well-studied wiggly optical light curve of GRB 030329, for which refreshed shocks provide the likeliest explanation [176]. Other ways to get light curve bumps which are not too steep after ~ hours to days is with micro-lensing [154, 173], late injection [522, 210], or inverse Compton effects [436, 523, 190]. The changes in the shock physics and dynamics in highly magnetized or Poynting dominated outflows were discussed, e.g. in [468, 465, 306, 174, 176, 279, 527]. More examples and references to departures from the standard model are discussed, e.g. in [471, 525]. Departures from spherical symmetry and jet effects are discussed in the next two subsections.

5.4. Equal arrival time surface and limb brightening effect

As illustrated in Figure 5, for a distant observer the photons from a spherically expanding shell are received from an equal-arrival time surface which is an ellipsoid (if = constant). The photons arriving from the line of sight originated at larger radii than photons arriving from the light-cone at ~ . At smaller radii the outflow had a higher magnetic field and higher density, so the radiation from the 1 / edge is harder and more intense. Thus an interesting effect, which arises even in spherical outflows, is that the effective emitting region seen by the observer resembles a ring [496, 168, 357, 434, 170]. This limb brightening effect is different in the different power law segments of the spectrum. When one considers the change in due to deceleration, the ellipsoid is changed into an egg shape, which is similarly limb-brightened. This effect is thought to be implicated in giving rise to the radio diffractive scintillation pattern seen in several afterglows, since this requires the emitting source to be of small dimensions (the ring width), e.g. in GRB 970508 [498]. This provided an important observational check, giving a direct confirmation of the relativistic source expansion and a direct determination of the (expected) source size [498, 219]. The above treatments were based on the simple asymptotic scaling behavior for the Lorentz factor ~ constant at r r_dec and r^-3/2 ( r^-3) at r r_dec for the adiabatic (fully radiative) cases (Section 4.5). More exact treatments are possible [41, 42] based on following analytically and numerically the detailed dynamical evolution equations for the Lorentz factor through and beyond the transition between pre-deceleration and post-deceleration. The shape of the equi-temporal surfaces is modified, and the expected light curves will be correspondingly changed. The exact afterglow behavior will depend on the unknown external medium density and on whether and what kind of continued of continued energy injection into the shock occurs, which introduces an additional layer of parameters to be fitted.

5.5. Jets

The spherical assumption is valid even when considering a relativistic outflow collimated within some jet of solid angle _j < 4, provided the observer line of sight is inside this angle, and _j^-1/2 [300], so the light-cone is inside the jet boundary (causally disconnected) and the observer is unaware of what is outside the jet. However, as the ejecta is decelerated, the Lorentz factor eventually drops below this value, and a change is expected in the dynamics and the light curves [408, 409]. It is thought that this is what gives rise to the achromatic optical light curve breaks seen in many afterglows [243, 135].

The jet opening angle can be obtained form the observer time t_j at which the flux F decay rate achromatically changes to a steeper value, assuming that this corresponds to the causal (light-cone) angle (t)^-1 having become comparable to (and later larger than) the jet half-angle _j [408]. Assuming a standard adiabatic dynamics and a uniform external medium, the jet opening half-angle is

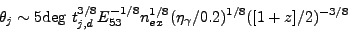(35)

where E₅₃ is the isotropic equivalent gamma-ray energy in ergs, t_j,d = t_j / day and is radiative efficiency [135]. The degree of steepening of the observed flux light curve can be estimated by considering that while the causal angle is smaller than the jet opening angle, the effective transverse area from which radiation is received is A ~ r² ~ (r / )² t^{2 2}, whereas after the causal angle becomes larger than the jet angle, the area is A ~ r² _j². Thus the flux after the break, for an adiabatic behavior t^-3/8 (valid if there is no sideways expansion) is steeper by a factor ² t^-3/4 [307], a value in broad agreement with observed breaks. After this time, if the jet collimation is simply ballistic (i.e. not due to magnetic or other dynamical effects) the jet can start expanding sideways at the comoving (relativistic) speed of sound, leading to a different decay t^-1/2 and F t^-p t^-2 [409].

A collimated outflow greatly alleviates the energy requirements of GRB. If the burst energy were emitted isotropically, the energy required spreads over many orders of magnitude, E_,iso ~ 10⁵¹ - 10⁵⁴ erg [243]. However, taking into account the jet interpretation of light curve breaks in optical afterglows [352, 135, 353] the spread in the total -ray energy is reduced to one order of magnitude, around a less demanding mean value of E_,tot ~ 1.3 × 10⁵¹ erg [51]. This is not significantly larger than the kinetic energies in core-collapse supernovae, but the photons are concentrated in the gamma-ray range, and the outflow is substantially more collimated than in the SN case. Radiative inefficiencies and the additional energy which must be associated with the proton and magnetic field components increase this value (e.g. the factor in equation [35]), but this energy is still well within the theoretical energetics 10^53.5 - 10⁵⁴ erg achievable in either NS-NS, NS-BH mergers [306] or in collapsar models [514, 346, 380] using MHD extraction of the spin energy of a disrupted torus and/or a central fast spinning BH. It is worth noting that jets do not invalidate the usefulness of spherical snapshot spectral fits, since the latter constrain only the energy per solid angle [309].

Equation (35) assumes a uniform external medium, which fits most afterglows, but in some cases a wind-like external medium (n_ext r^-2) is preferred [351, 66, 267]. For an external medium varying as n_ext = Ar^-k one can show that the the Lorentz factor initially evolves as (E / A)^1/2 r^-(3-k)/2 (E / A)^1/(8-2k) t^{-(3-k)/(8-2k)}, and the causality (or jet break) condition ~ _j^-1 leads to a relation between the observed light curve break time t_j and the inferred collimation angle _j which is different from equation (35), namely _j (E / A)^-1/(8-2k) (t_j / [1 + z])^(3-k)/(8-2k) (E / A)^-1/4 (t_j / [1 + z])^1/4, where the last part is for k = 2. Another argument indicating that the medium in the vicinity of at least some long-GRB afterglows is not stratified, e.g. as r^-2, is the observation of a sharp jet-break in the optical afterglow lightcurves (as, e.g. in GRB 990510, 000301c, 990123). As pointed out by [248], relativistic jets propagating in a wind-like external medium are expected to give rise to a very gradual and shallow break in the afterglow lightcurve.

The discussion above also makes the simplifying assumption of a uniform jet (uniform energy and Lorentz factor inside the jet opening angle, or top-hat jet model). In this case the correlation between the inverse beaming factor f_b^-1 = (_j² / 2)^-1 (or observationally, the jet break time from which _j is derived) and the isotropic equivalent energy or fluence E_,iso is interpreted as due to a distribution of jet angles, larger angles leading to lower E_,iso, according to E_{,iso j}^-2. There is, however, an equally plausible interpretation for this correlation, namely that one could have a universal jet profile such that the energy per unit solid angle dE / d ^-2, where is the angle measured from the axis of symmetry [414, 524]. (To avoid a singularity, one can assume this law to be valid outside some small core solid angle). This model also explains the [135, 352] correlation, the different E_iso would be due to the observer being at different angles relative to the jet axis. This hypothesis has been tested in a variety of ways [186, 324, 249, 178]. Attempts to extend the universal ^-2 jet structure to include X-ray flashes (Section 2.5), together with use of the Amati relation between the spectral peak energy E_peak and E_,iso (Section 2.6), leads to the conclusion that a uniform top-hat model is preferred over a universal ^-2 jet model [250]. Uniform jets seen off-axis have also been considered as models for XRF in a unified scheme, e.g. [517, 181]. On the other hand, another type of universal jet profile with a Gaussian shape [520, 85] appears to satisfy both the jet break-E_,iso and E_peak - E_,iso correlations for both GRB and XRFs. More extensive discussion of this is in [525].

The uniform and structured jets are expected to produce achromatic breaks in the light curves, at least for wavebands not too widely separated. However, in some bursts there have been indications of different light curve break times for widely separated wavebands, e.g. GRB 030329, suggesting different beam opening angles for the optical/X-ray and the radio components [37]. Such two-component jets could arise naturally in the collapsar model, e.g. with a narrow, high Lorentz factor central jet producing , X-ray and optical radiation, and a wider slower outflow, e.g. involving more baryon-rich portions of the envelope producing radio radiation [392]. A wider component may also be connected to a neutron-rich part of the outflow [370]. More recent discussions of possible chromatic breaks are in [113, 361].