6. CURRENT THEORETICAL ISSUES IN AFTERGLOW MODELS

The afterglow is generally assumed to become important after the time when the self-similar r^-3/2 behavior starts. From equation (19 for the deceleration time t_dec~ (r_dec / 2c ²) and taking into account the gradual transition to the self-similar regime [235], this is approximately

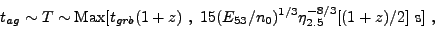(36)

where t_grb is the duration of the outflow, i.e. an upper limit for the duration of the prompt -ray emission, and a cosmological time dilation factor is included. (Note that in some bursts the -rays could continue in the self-similar phase). The afterglow emission from the forward and the reverse shock emission starts immediately after the ejecta starts to sweeps up matter, but it does not peak (and become dominant over the prompt emission or its decaying tail) until the time ~ t_ag, marking the beginning of the self-similar blast wave regime.

Denoting the frequency and time dependence of the afterglow spectral energy flux as F(t) ^- t^-, the late X-ray afterglow phases (3) and (4) of Section 3 seen by Swift are similar to those known previously from Beppo-SAX (the theoretical understanding of which is discussed in Section 5 and in [525]). The "normal" decay phase (3), with temporal decay indices ~ 1.1 - 1.5 and spectral energy indices ~ 0.7 - 1.0, is what is generally expected from the evolution of the forward shock in the Blandford-McKee self-similar late time regime, under the assumption of synchrotron emission.

6.1. Early steep decay

Among the new afterglow features detected by Swift (see Figure 3), the steep initial decay phase F t^-3 - t^-5 in X-rays of the long GRB afterglows is one of the most striking. There are several possible mechanisms which could cause this. The most obvious first guess would be to attribute it to the cooling following cessation of the prompt emission (internal shocks or dissipation). If the comoving magnetic field in the emission region is random [or transverse], the flux per unit frequency along the line of sight in a given energy band, as a function of the electron energy index p, decays as F t^- with = -2p [(1 - 3p) / 2] in the slow cooling regime, where = (p - 1) / 2, and it decays as = -2(1 + p), [-(2 - 3p) / 2] in the fast cooling regime where = p / 2, i.e. for the standard p = 2.5 this would be = -5,[-3.25] in the slow cooling or = -7, [-2.75] in the fast cooling regime, for random [transverse] fields [307]. In some bursts this may be the explanation, but in others the time and spectral indices do not correspond well. In addition, if the flux along the line of sight decays as steeply as above, the observed flux would be dominated by the so-called high latitude emission, which is discussed next.

At present, the most widely considered explanation for the fast decay, both of the initial phase (1) and of the steep flares, attributes it to the off-axis emission from regions at > ^-1 (the curvature effect, or high latitude emission [226]. In this case, after the line of sight gamma-rays have ceased, the off-axis emission observed from > ^-1 is ( )^-6 smaller than that from the line of sight. Integrating over the equal arrival time region, this flux ratio becomes ( )^-4. Since the emission from arrives ( )² later than from = 0, the observer sees the flux falling as F t^-2, if the flux were frequency independent. For a source-frame flux '^-, the observed flux per unit frequency varies then as

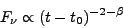(37)

i.e. = 2 + . This "high latitude" radiation, which for observers outside the line cone at > ^-1 would appear as prompt -ray emission from dissipation at radius r, appears to observers along the line of sight (inside the light cone) to arrive delayed by t ~ (r² / 2 c) relative to the trigger time, and its spectrum is softened by the Doppler factor t^-1 into the X-ray observer band. For the initial prompt decay, the onset of the afterglow (e.g. phases 2 or 3), which also come from the line of sight, may overlap in time with the delayed high latitude emission. In equation (37) t₀ can be taken as the trigger time, or some value comparable or less than equation (36). This can be used to constrain the prompt emission radius [257]. When t_dec < T, the emission can have an admixture of high latitude and afterglow, and this can lead to decay rates intermediate between the two [340]. Values of t₀ closer to the onset of the decay also lead to steeper slopes. It is possible to identify for various bursts values of t₀ near the rising part of the last spike in the prompt emission which satisfy the subsequent steep decay slope [270]. Structured jets, when viewed on-beam produce essentially the same slopes as homogeneous jets, while off-beam observing can lead to shallower slopes [103]. For the flares, if their origin is assumed to be internal (e.g. some form of late internal shock or dissipation) the value of t₀ is just before the flare, e.g the observer time at which the internal dissipation starts to be observable [526]. This interpretation appears, so far, compatible with most of the Swift afterglows [528, 338, 360].

Alternatively, the initial fast decay may be due to the emission of a cocoon of exhaust gas [368], where the temporal and spectral index are explained through an approximately power-law behavior of escape times and spectral modification of multiply scattered photons. The fast decay may also be due to the reverse shock emission, if inverse Compton up-scatters primarily synchrotron optical photons into the X-ray range. The decay starts after the reverse shock has crossed the ejecta and electrons are no longer accelerated, and may have both a line of sight and an off-axis component [234]. This poses strong constraints on the Compton-y parameter, and cannot explain decays much steeper than = -2, or -2 - if the off-axis contribution dominates. Models involving bullets, whose origin, acceleration and survivability is unexplained, could give a prompt decay index ~ -3 to -5 [79], with a bremsstrahlung energy index ~ 0 which is not observed in the fast decay; switching to a synchrotron or IC mechanisms requires additional parameters. Finally, a patchy shell model, where the Lorentz factor is highly variable in angle, would produce emission with ~ -2.5. Thus, such mechanisms may explain the more gradual decays, but not the more extreme = -5,-7 values encountered in some cases. It should be noted, however, that the Swift X-ray observations suggest that the steep decay is a direct continuation of the prompt emission [340], which in turn suggests that the prompt and the fast decaying emission arise from the same physical region, posing a problem for the models in this paragraph (but not for the high latitude emission model).

6.2. Shallow decay

The slow decay portion of the X-ray light curves ( ~ -0.3-0.7), ubiquitously detected by Swift, is not entirely new, having been detected in a few cases by BeppoSAX. This, as well as the appearance of wiggles and flares in the X-ray light curves after several hours were the motivation for the "refreshed shock" scenario [405, 437] (Section 5.3). Refreshed shocks can flatten the afterglow light curve for hours or days, even if the ejecta is all emitted promptly at t = T t, but with a range of Lorentz factors, say M() ^-s, where the lower shells arrive much later to the foremost fast shells which have already been decelerated. Thus, for an external medium of density r^-k and a prompt injection where the Lorentz factor spread relative to ejecta mass and energy is M() ^-s, E() ^-s+1, the forward shock flux temporal decay is given by [437]

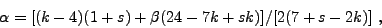(38)

(for more details, see Table 1). It needs to be emphasized that in this model all the ejection can be prompt (e.g. over the duration ~ T of the gamma ray emission) but the low portions arrive at (and refresh) the forward shock at late times, which can range from hours to days. I.e., it is not the central engine which is active late, but its effects are seen late. Fits of such refreshed shocks to observed shallow decay phases in Swift bursts [180] lead to a distribution which is a broken power law, extending above and below a peak around ~ 45.

There is a different version of refreshed shocks, which does envisage central engine activity extending for long periods of time, e.g. day (in contrast to the minutes engine activity in the model above). Such long-lived activity may be due to continued fall-back into the central black hole [513] or a magnetar wind [522, 83, 338]. One characteristic of both types of refreshed models is that after the refreshed shocks stop and the usual decay resumes, the flux level shows a step-up relative to the previous level, since new energy has been injected.

From current analyses, the refreshed shock model is generally able to explain the flatter temporal X-ray slopes seen by Swift, both when it is seen to join smoothly on the prompt emission (i.e. without an initial steep decay phase) or when seen after an initial steep decay. Questions remain concerning the interpretation of the fluence ratio in the shallow X-ray afterglow and the prompt gamma-ray emission, which can reach 1 [340]. This requires a higher radiative efficiency in the prompt gamma-ray emission than in the X-ray afterglow. One might speculate that this might be achieved if the prompt outflow is Poynting-dominated, or if a more efficient afterglow hides more of its energy in other bands, e.g. in GeV, or IR. Alternatively [211, 182], a previous mass ejection might have emptied a cavity into which the ejecta moves, leading to greater efficiency at later times (although this would not work above the cooling frequency, which from the spectrum appears to be required in about half the cases), or otherwise the energy fraction going into the electrons increases t^1/2. Other possible ways of addressing this include the afterglow coming from off-axis directions [104], and exploring plausible reasons for having underestimated in previous studies the energy of the ejecta [182].

6.3. X-ray flares

Refreshed shocks can also explain some of the X-ray flares whose rise and decay slopes are not too steep. However, this model encounters difficulties with the very steep flares with rise or decay indices ~ ± 5, ± 7, such as inferred from the giant flare of GRB 050502b [57] around 300 s after the trigger. Also, the flux level increase in this flare is a factor ~ 500 above the smooth afterglow before and after it, implying a comparable energy excess in the low versus high material. An explanation based on inverse Compton scattering in the reverse shock [234] can explain a single flare at the beginning of the afterglow, with not too steep decay. For multiple flares, models invoking encountering a lumpy external medium have generic difficulties explaining steep rises and decays [323, 528], although extremely dense, sharp-edged lumps, if they exist, might satisfy the steepness [99].

Currently the more widely considered model for the flares ascribes them to late central engine activity [528, 338, 360]. The strongest argument in favor of this is that the energy budget is more easily satisfied, and the fast rise/decay is straightforward to explain. In such a model the flare energy can be comparable to the prompt emission, the fast rise comes naturally from the short time variability leading to internal shocks (or to rapid reconnection), while the rapid decay may be due to the high latitude emission following the flare, with t₀ reset to the beginning of each flare (see further discussion in [526]). However, some flares are well modeled by refreshed forward shocks, while in others this is clearly ruled out and a central engine origin is better suited [516]. Aside from the phenomenological desirability based on energetics and timescales, a central engine origin is conceivable, within certain time ranges, based on numerical models of the burst origin in long bursts. These are interpreted as being due to core collapse of a massive stellar progenitor, where continued infall into fast rotating cores can continue for a long time [513]. However, large flares with a fluence which is a sizable fraction of the prompt emission occurring hours later remain difficult to understand. It has been argued that gravitational instabilities in the infalling debris torus can lead to lumpy accretion [371]. Alternatively, if the accreting debris torus is dominated by MHD effects, magnetic instabilities can lead to extended, highly time variable accretion [384], which may give rise to GRB X-ray flares [386].

6.4. Late steep decay and jet breaks

The late steep decay decay phase (4) of Section 3 is seen in a modest fraction of the Swift bursts, mainly in X-rays, and mainly but not exclusively in long bursts. The natural interpretation is that these are caused by the fact that the outflow is collimated into a jet break: when the decrease of the ejecta Lorentz factor leads to the light-cone angle becoming larger than the jet angular extent, _j(t) 1 / _j (e.g. Section 5.5), the light curve steepens achromatically. For the Swift bursts, it is noteworthy that this final steepening has been seen in less than ~ 10% of the afterglows followed, and then with reasonable confidence mainly in X-rays. The corresponding optical light curve breaks have been few, and not well constrained. The UVOT finds afterglows in only ~ 30% of the bursts, and ground-based optical/IR telescopes have yielded few continued late time light curves monitored. This is unlike the case with the ~ 20 Beppo-SAX bursts, for which an achromatic break was reported in the optical [135], while in rarer cases there was an X-ray or radio break reported, which in a few cases appeared to occur at a different time than the optical break (e.g. [36]).

The relative paucity of optical breaks in Swift afterglows may be an observational selection effect due to the larger median redshift, and hence fainter and redder optical afterglow at the same observer epoch. At higher redshifts the break occurs later in the observer frame, which compounds a possible reluctance to commit large telescope time on more frequently reported bursts (roughly 2/week from Swift versus an earlier 2/month with Beppo-SAX). One can speculate that the apparent scarcity of detected light curve breaks might indicate that at higher redshifts the opening angle is intrinsically larger. However, continued monitoring of the X-ray light curves with both Swift and Chandra is resulting in a growing number of bursts with high quality late X-ray light curves showing in some cases a clear break, and others the absence of a break up to weeks (also in short bursts, e.g. [59, 184]). This is an evolving topic, with some indications that light curve breaks may not (or not always) appear achromatic [113, 361].

6.5. Prompt optical flashes and high redshift afterglows

Optical/UV afterglows have been detected with the Swift UVOT telescope in roughly half the bursts for which an X-ray afterglow was seen. For a more detailed discussion of the UVOT afterglow observations see [411]. Of particular interest is the ongoing discussion on whether "dark GRB" are really optically deficient, or the result of observational bias [40]. Another puzzle is the report of a bimodal intrinsic brightness distribution in the rest-frame R-band [269, 333]. This suggests possibly the existence of two different classes of long bursts, or at least two different types of environments.

Compared to a few years ago, a much larger role is being played by ground-based robotic optical follow-ups, due to the increased rate of several arc-second X-ray alerts from XRT, and the larger number of robotic telescopes brought on-line in the last years. For the most part, these detections have yielded optical decays in the few 100 s range, initial brightness m_V ~ 14-17 and temporal decay slopes ~ 1.1-1.7 previously associated with the evolution of a forward shock [131, 39]. In a few cases, a prompt optical detection was achieved in the first 12-25 s [428, 429, 480].

The most exciting prompt robotic IR detection (and optical non-detection) is that of GRB 050904 [54, 188]. This object, at the unprecedented high redshift of z = 6.29 [220], has an X-ray brightness exceeding for a day that of the brightest X-ray quasars (see Figure 8) [491]. Its O/IR brightness in the first 500 s (observer time) was comparable to that of the extremely bright (m_V ~ 9) optical flash in GRB 990123, with a similarly steep time-decay slope ~ 3 [54]. Such prompt, bright and steeply decaying optical emission is expected from the reverse shock as it crosses the ejecta, marking the start of the afterglow [305, 441, 307].

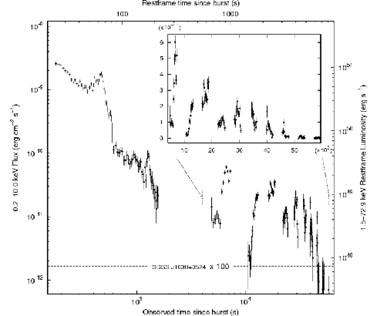Figure 8. The X-ray afterglow of the GRB 050904 at z = 6.29 [491], showing for comparison the flux level of one of the most lumnious X-ray quasars at a comparable redshift, SDSS J1030+0524 (multiplied by 100). The inset shows the GRB variability in the 10-70 ks timeframe.

However, aside from the two glaring examples of 990123 and 050904, in the last six years there have been less than a score of other prompt optical flashes, typically with more modest initial brightnesses m_v 13. There are a number of possible reasons for this paucity of optically bright flashes, if ascribed to reverse shock emission. One is the absence or weakness of a reverse shock, e.g. if the ejecta is highly magnetized [305]. A moderately magnetized ejecta is in fact favored for some prompt flashes [521]. Alternatively, the deceleration might occur in the thick-shell regime (T >> t_dec. see eq. (36), which can result in the reverse shock being relativistic, boosting the optical reverse shock spectrum into the UV [231] (in this case a detection by UVOT might be expected, unless the decay is faster than the typical 100-200 s for UVOT slewing and integration). Another possibility, for a high comoving luminosity, is copious pair formation in the ejecta, causing the reverse shock spectrum to peak in the IR [312]. Since both GRB 990123 and GRB 050904 had E_iso ~ 10⁵⁴ erg, among the top few percent of all bursts, the latter is a distinct possibility, compatible with the fact that the prompt flash in GRB 050904 was bright in the IR I-band but not in the optical. On the other hand, the redshift z = 6.29 of this burst, and a Ly- cutoff at ~ 800 nm would also ensure this (and GRB 990123, at z = 1.6, was detected in the V-band). However, the observations of optical flashes in these two objects but not in lower E_iso objects appears compatible with having a relativistic (thick shell) reverse shock with pair formation. Even in the absence of pairs, more accurate calculations of the reverse shock [326, 290] find the emission to be significantly weaker than was estimated earlier. Another possibility is that the cooling frequency in reverse shock is typically not much larger than the optical band frequency. In this case the optical emission from the reverse shock drops to zero very rapidly soon after the reverse shock has crossed the ejecta and the cooling frequency drops below the optical and there are no electrons left to radiate in the optical band [290].