As the Universe evolved from its early, hot, dense beginnings (the "Big Bang") to its present, cold, dilute state, it passed through a brief epoch when the temperature (average thermal energy) and density of its nucleon component were such that nuclear reactions building complex nuclei could occur. Because the nucleon content of the Universe is small (in a sense to be described below) and because the Universe evolved through this epoch very rapidly, only the lightest nuclides (D, 3He, 4He, and 7Li) could be synthesized in astrophysically interesting abundances. The relic abundances of these nuclides provide probes of conditions and contents of the Universe at a very early epoch in its evolution (the first few minutes) otherwise hidden from our view. The standard model of Cosmology subsumes the standard model of particle physics (e.g., three families of very light, left-handed neutrinos along with their right-handed antineutrinos) and uses General Relativity (e.g., the Friedman equation) to track the time-evolution of the universal expansion rate and its matter and radiation contents. While nuclear reactions among the nucleons are always occurring in the early Universe, Big Bang Nucleosynthesis (BBN) begins in earnest when the Universe is a few minutes old and it ends less than a half hour later when nuclear reactions are quenched by low temperatures and densities. The BBN abundances depend on the conditions (temperature, nucleon density, expansion rate, neutrino content and neutrino-antineutrino asymmetry, etc.) at those times and are largely independent of the detailed processes which established them. As a consequence, BBN can test and constrain the parameters of the standard model (SBBN), as well as probe any non-standard physics/cosmology which changes those conditions.
The relic abundances of the light nuclides synthesized in BBN depend on
the competition between the nucleon density-dependent nuclear reaction
rates and the universal expansion rate. In addition, while all
primordial abundances depend to some degree on the initial (when BBN
begins) ratio of neutrons to protons, the 4He abundance is
largely fixed by this ratio, which is determined by the competition between
the weak interaction rates and the universal expansion rate, along
with the magnitude of any
e -
e asymmetry.
1 To summarize, in its
simplest version BBN depends on three unknown parameters: the baryon
asymmetry; the lepton asymmetry; the universal expansion rate. These
parameters are quantified next.
1.1. Baryon Asymmetry - Nucleon Abundance
In the very early universe baryon-antibaryon pairs (quark-antiquark pairs)
were as abundant as radiation (e.g., photons). As the Universe
expanded and
cooled, the pairs annihilated, leaving behind any baryon excess
established during the earlier evolution of the Universe
[1].
Subsequently, the number of baryons in a comoving volume of the Universe
is preserved. After e ± pairs annihilate, when the
temperature (in energy
units) drops below the electron mass, the number of Cosmic Background
Radiation (CBR) photons in a comoving volume is also preserved. As a
result, it is useful (and conventional) to measure the universal baryon
asymmetry by comparing the number of (excess) baryons to the number
of photons in a comoving volume (post-e ±
annihilation). This ratio defines the baryon abundance parameter
B,
 |
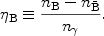(1) |
As will be seen from BBN, and as is confirmed by a variety of
independent (non-BBN), astrophysical and cosmological data,
B
is very small. As a result, it is convenient to introduce
10
1010
B
and to use it
as one of the adjustable parameters for BBN. An equivalent measure
of the baryon density is provided by the baryon density parameter,
ΩB, the ratio (at present) of the baryon mass density
to the critical density. In terms of the present value of the Hubble
parameter (see Section 1.2 below), H0
100 h km
s-1 Mpc-1, these two measures are related by
 |
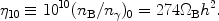(2) |
Note that the subscript 0 refers to the present epoch (redshift z = 0).
From a variety of non-BBN cosmological observations whose accuracy
is dominated by the very precise CBR temperature fluctuation data
from WMAP
[2],
the baryon abundance parameter is limited to a narrow range centered near
10
6. As a result,
while the behavior of the BBN-predicted relic abundances will be
described qualitatively as functions of
B,
for quantitative comparisons the results presented here will focus on
the limited interval 4 
10
8. As will be seen below
(Section 2.2), over this range there
are very simple, yet accurate, analytic fits to the BBN-predicted
primordial abundances.
1.2. The Expansion Rate At BBN
For the standard model of cosmology, the Friedman equation relates the expansion rate, quantified by the Hubble parameter (H), to the matter-radiation content of the Universe.
 |
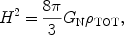(3) |
where GN is Newton's gravitational constant. During the
early evolution of the Universe the total density,
TOT,
is dominated by "radiation" (i.e., by the contributions from
massless and/or extremely relativistic particles). During radiation
dominated epochs (RD), the age of the Universe (t) and the Hubble
parameter are simply related by (Ht)RD = 1/2.
Prior to BBN, at a temperature of a few MeV, the standard model of
particle physics determines that the relativistic particle content
consists of photons, e ± pairs and three flavors
of left-handed (i.e., one helicity state) neutrinos (along with
their right-handed, antineutrinos;
N = 3). With all
chemical potentials set
to zero (very small lepton asymmetry) the energy density of these
constituents in thermal equilibrium is
 |
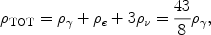(4) |
where 
is the
energy density in the CBR photons (which
have redshifted to become the CBR photons observed today at a temperature
of 2.7K). In this case (SBBN:
N = 3), the
time-temperature relation derived from the Friedman equation is,
 |
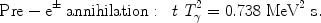(5) |
In SBBN it is usually assumed that the neutrinos are fully decoupled
prior to e ± annihilation; if so, they don't share
in the energy transferred from the annihilating
e ± pairs to the CBR photons. In
this very good approximation, the photons are hotter than the neutrinos
in the post-e ± annihilation universe by a factor
T /
T =
(11/4)1/3, and the total energy density is
 |
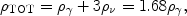(6) |
corresponding to a modified time-temperature relation,
 |
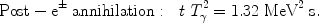(7) |
Quite generally, new physics beyond the standard models of cosmology or particle physics could lead to a non-standard, early Universe expansion rate (H'), whose ratio to the standard rate (H) may be parameterized by an expansion rate factor S,
 |
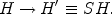(8) |
A non-standard expansion rate might originate from modifications to
the 3+1 dimensional Friedman equation as in some higher dimensional
models
[3],
or from a change in the strength of gravity
[4].
Different gravitational couplings for fermions and bosons
[5]
would have similar effects. Alternatively, changing the particle
population in early Universe will modify the energy density - temperature
relation, also leading, through eq. 3, to S
1. While
these different mechanisms for implementing a non-standard expansion
rate are not necessarily equivalent, specific models generally lead
to specific predictions for S.
Consider, for example, the case of a non-standard energy density.
 |
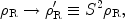(9) |
where
'R =
R +
X
and X identifies
the non-standard component. With the restriction that the X
are relativistic, this extra component, non-interacting at
e ± annihilation, behaves as would an additional
neutrino flavor. It must be emphasized that X is not
restricted to additional flavors of active or sterile neutrinos. In this
class of models S is constant prior to e ±
annihilation and it is convenient
(and conventional) to account for the extra contribution to the
standard-model energy density by normalizing it to that of an
"equivalent" neutrino flavor
[6],
so that
 |
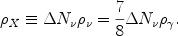(10) |
For this case,
 |
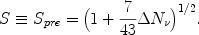(11) |
In another class of non-standard models the early Universe is
heated by the decay of a massive particle, produced earlier in the evolution
[7].
If the Universe is heated to a temperature which is too low to
(re)populate a thermal spectrum of the standard neutrinos
(TRH
7 MeV), the
effective number of neutrino flavors contributing to the total energy
density is < 3, resulting in
N < 0 and
S < 1.
Since the expansion rate is more fundamental than is
N,
BBN for models with non-standard expansion rates will be parameterized
using S (but, for comparison, the corresponding value of
N from
eq. 11 will often be given for comparison). The simple,
analytic fits to BBN presented below
(Section 2.2) are quite accurate for
0.85 S
1.15, corresponding to -1.7
N
2.0
The baryon asymmetry of the Universe, quantified by
B,
is very small. If, as expected in the currently most popular particle
physics models, the universal lepton and baryon numbers are comparable,
then any asymmetry between neutrinos and antineutrinos ("neutrino
degeneracy") will be far too small to have a noticeable effect on
BBN. However, it is possible that the baryon and lepton asymmetries
are disconnected and that the lepton (neutrino) asymmetry could be large
enough to perturb the SBBN predictions. In analogy with
B
which quantifies the baryon asymmetry, the lepton (neutrino) asymmetry,
L = L
L, may be
quantified by the neutrino chemical potentials µ
(
e, µ, 
)
or, by the degeneracy parameters, the ratios of the
neutral lepton chemical potentials to the temperature (in energy units)
µ / kT,
where
 |
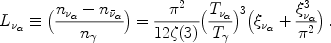(12) |
Prior to e ± annihilation,
T =
T,
while post-e ± annihilation
(T /
T)3 = 4/11. Although in principle
the asymmetry among the different neutrino flavors may be different,
mixing among the three active neutrinos
(e,
µ,
)
ensures that at BBN, Le
Lµ
L
(e
µ
)
[8].
If L is
measured post-e ± annihilation, as is
B,
then for
<< 1,
L
3Le
and, for
e
<< 1,
L
0.75.
Although any neutrino degeneracy
( < 0 as well
as > 0) increases the energy density in the relativistic
neutrinos, resulting in an effective
N
0 (see eq. 10), the
range of || of
interest to BBN is limited to sufficiently small
values that the increase in S due to a non-zero
is negligible.
However, a small asymmetry between electron type neutrinos and
antineutrinos
(e
10-2;
L
0.007), while large
compared to the baryon asymmetry, can have a significant impact on
BBN since the e
affect the interconversion of neutrons to protons. A non-zero
e
results in different (compared to
SBBN) numbers of e
and e,
altering the n/p ratio at BBN, thereby changing the yields (compared to
SBBN) of the light nuclides.
Of the light, relic nuclei, the neutron limited 4He
abundance is most sensitive to a non-zero
e;
4He is a good "leptometer". In concert with the abundances of
D, 3He, and 7Li, which are good
baryometers, the 4He abundance provides a test of the
consistency of the standard model along with constraints on non-standard
models. The analytic fits presented below
(Section 2.2) are reasonably accurate
for e
in the range, -0.1
e
0.1, corresponding
to a total lepton number limited to |L|
0.07. While this
may seem small, recall that a similar measure of the baryon asymmetry is
orders of magnitude smaller:
B
6 ×
10-10.
1 A lepton asymmetry much larger than the baryon asymmetry (which is very small; see Section 1.1 below) would have to reside in the neutrinos since charge neutrality ensures that the electron-positron asymmetry is comparable to the baryon asymmetry. Back.