So far, we have not considered how a galaxy converts its available gas into stars and what effect those stars, and associated supernovae explosions, may have on the evolution of the galaxy. Additionally, observational evidence suggests that all galaxies contain a supermassive black hole at their center, which may play a key role in limiting the process of galaxy formation. We will discuss these aspects of galaxy formation theory below. We do not explore in detail the role of the associated galactic winds in galaxy evolution, but refer the reader to Veilleux et al. (2005) for a thorough review.
Star formation theory warrants an entire review to itself (for a recent example see McKee and Ostriker 2007) and so we will summarize only those aspects most pertinent to galaxy formation theory. The past decade has seen a greatly improved understanding of how the key processes of turbulence, magnetic fields and self-gravity interact to form molecular clouds and stars. Nevertheless, there remain numerous unsolved problems in star formation theory. These problems propagate into galaxy formation theory if we wish to understand the rate at which stars form in a galaxy and any consequences that may have for further galactic evolution. This problem is somewhat mitigated by the fact that, for galaxy formation theory, we do not necessarily care about the details of how stars form. Instead, we would simply like to know, given the large scale properties of a galaxy (e.g. mass, size, density, dynamical time, gas fraction, chemical composition), what is the resulting rate of star formation.
Traditionally, this question has been answered by appealing to empirical
rules or dimensional analysis. For example, much use has been made of
the empirically derived scaling relations of
Schmidt
(1959)
and Kennicutt
(1989,
1998).
The Schmidt-Kennicutt law states that the rate of star formation per
unit surface area,
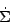*, depends on the surface density
of gas,
gas as
 |
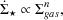(81) |
where n is measured to be approximately 1.4. While this relation is practically useful for galaxy formation theory, insofar as it allows one to bypass the question of star formation and move directly to a star formation rate, it suffers from the same issue as all empirical relations used in theoretical models: there is no way to be sure that it is valid beyond the regimes where it was originally measured.
Recently, new observations have suggested a relatively simple model for
star formation
(Krumholz
and Tan 2007).
Stars form in molecular clouds and so it is natural that it would be the
density of molecular gas (rather than total) gas which
matters. Furthermore, it is observed that a constant fraction (around
2%) of molecular gas turns into stars per free-fall timescale. This
implies
* =
ff
fH2
gas
/ tff where
ff is the
fraction of molecular gas turned into stars per free-fall time,
fH2 is the molecular fraction and
tff is the local free-fall timescale.
In the model of Robertson and Kravtsov (2008, see also Krumholz et al. 2009) the star formation rate is given by
 |
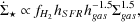(82) |
where fH2 is the fraction of hydrogen in molecular form, hSFR is the scale height of the star-forming gas and hgas is the scale height of the interstellar medium. Robertson and Kravtsov (2008) compute fH2 and the scale height self-consistently in the presence of the interstellar radiation field produced by earlier generations of stars. This results in a net scaling with total gas surface density of
 |
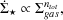(83) |
where ntot
2 for massive
galaxies and ntot
4 for dwarf
galaxies. When expressed in terms of the molecular hydrogen gas surface
density a scaling
 |
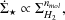(84) |
with nmol
1.3 is found for all
galaxies. These scalings are consistent with a broad range of
observations of star formation in different galaxies.
Similarly, Krumholz et al. (2009) find that the following expression encapsulates the complex physics of star formation:
 |
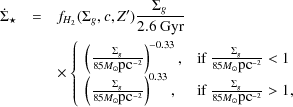(85) |
where the molecular hydrogen fraction is
 |
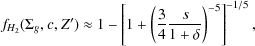(86) |
and s = ln(1 + 0.6
)
/ (0.04comp,0
Z' ), = 0.77(1 +
3.1Z' 0.365),
=
0.0712(0.1s-1 + 0.675)-2.8,
comp,0 =
comp /
( 1M
pc-2) and Z' is the metallicity normalized
to the Solar value. The transition at gas surface densities of 85
M
pc-2 corresponds to the point at which the ambient pressure
becomes comparable to the internal pressure in molecular clouds (and
therefore influences the properties of those molecular clouds). Here,
comp is
the surface density of a ~ 100 pc-sized
atomic-molecular complex. Since simulations and semi-analytic models
typically only predict the gas distribution on scales significantly
larger than this we can write
comp =
cg
where c is a clumping factor that
accounts for structures which are unresolved in the simulation. This
clumping factor should approach unity as the resolution approaches 100
pc at which point molecular cloud complexes should be adequately
resolved.
Over the past ten years it has become possible to measure the masses of supermassive black holes residing at the centers of galaxies for relatively large samples. The existence of strong correlations between the masses of these black holes and the properties of their host galaxy - such as spheroid mass (Magorrian et al. 1998), velocity dispersion (Ferrarese and Merritt 2000; Gebhardt et al. 2000a, b), number of globular clusters (Burkert and Tremaine 2010) or even host dark matter halo (Ferrarese 2002) - is suggestive of some interaction between forming galaxies and supermassive black holes. Of course, correlation does not imply causation (Munroe 2009) and Jahnke and Maccio (2010) show that a black hole-host galaxy mass relation can arise from uncorrelated initial conditions via simple merging, but the theoretical need for large amounts of energy to inhibit galaxy formation in massive halos naturally leads to the idea that supermassive black holes (SMBH) and galaxy formation are connected (Benson et al. 2003). In addition, understanding the formation of these most massive of black holes is interesting in its own right and has important observational consequences for both studies of active galactic nuclei and gravitational wave detection experiments such as the Laser Interferometer Space Antenna 24.
In light of these reasons, several studies have attempted to follow the process of SMBH formation within forming galaxies (Silk and Rees 1998; Monaco et al. 2000; Kauffmann and Haehnelt 2000; King 2003; Wyithe and Loeb 2003; Matteo et al. 2003; Volonteri et al. 2003; King 2005; Begelman and Nath 2005; Malbon et al. 2007; Matteo et al. 2008; Volonteri et al. 2008; Sijacki et al. 2009; Volonteri and Natarajan 2009). We will not review all details of this process here. Instead, we will focus on the basic formation mechanisms and, in Section 6.3.2, on the interaction between SMBHs and galaxy.
Before supermassive black holes can grow via accretion or merging, there must be some pre-existing (probably not supermassive) seed black holes. Most plausibly, these seeds form at high redshifts as the remnants of the earliest generation of Population III stars which have reached the end of their stellar lifetimes. Details of the formation of these first stars remain incompletely understood, but hydrodynamical simulations suggest that they have masses in the range of a few hundred Solar masses (Abel et al. 2002; Bromm et al. 2002), leaving intermediate mass black hole remnants.
To determine the rate at which gas accretes onto a black hole (or, more precisely, the black hole and any associated accretion disk system) we must consider how the black hole affects the gas through which it is moving. The gravity of a fast moving black hole will deflect gas that passes by it, focusing it into a wake behind the black hole which will then accrete onto the black hole. This problem, and the equivalent for a slowly (subsonically) moving black hole, was first studied by Hoyle and Lyttleton (1939) and Bondi and Hoyle (1944). This leads to an accretion rate of
 |
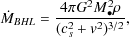(87) |
where
M
is
the mass of the black hole,
cs is the sound speed and v the relative
velocity of black hole and gas. The accretion occurs from a
characteristic radius of
 |
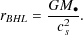(88) |
An in-depth review of Bondi-Hoyle-Lyttleton accretion is given by
Edgar
(2004).
The growth of black holes will be enhanced by any process which
increases the density in the central regions of the galaxy in which they
reside. At early times, this may occur due to gravitationally unstable
disks forming bars and driving gas towards the center
(Volonteri et al. 2008),
while at later times galaxy-galaxy mergers can results in dissipation
and gas flows to the center
(Matteo et
al. 2005).
Other mechanisms for delivering gas to the centers of galaxies are also
possible, for example
McKernan et
al. (2010)
show that warm clouds from the surrounding halo occasionally impact
galactic centers, potentially delivering 104-106
M of gas.
Bondi-Hoyle-Lyttleton accretion causes gas to flow towards the black hole. At some point, the angular momentum of the gas will become important and the accreting gas must form a disk. The final stage of accretion is then governed by this accretion disk, which may be a geometrically thin, radiative (Shakura and Sunyaev 1973) or a geometrically thick, radiatively inefficient (e.g. ADAF) flow (Narayan and Yi 1994). The details of the flow may be important for determining the spin of the black hole (see below) and the effects of feedback from any nuclear activity (see Section 6.3.2).
Galaxy-galaxy mergers can also lead to galaxies containing two (or potentially more) SMBHs, resulting in the potential for black hole mergers. The process of bringing two SMBHs together begins by dynamical friction against the background of dark matter (the same process which is causing the black hole host galaxies to merge). The subsequent merging process was originally outlined by Begelman et al. (1980) and assumes that the two black holes form a binary system at an initial separation of
 |
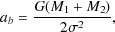(89) |
where M1 > M2 are the masses of
the black holes and 
is
the velocity dispersion of the host
galaxy, such that the binary orbit contains a mass in stars and dark
matter comparable to the sum of the black holes masses. Around this
binary, the stellar distribution is expected to form a cusp with density
profile *∝ r-7/4
(Bahcall
and Wolf 1976).
Initially, the binary hardens due to dynamical friction against the
stellar background acting on each black hole individually. As the binary
hardens this process becomes less effective as perturbations from
distant stars tend to perturb the center of mass of the binary without
changing its semi-major axis. However, once the binary becomes
sufficiently hard, at a separation of
(Quinlan 1996)
 |
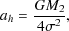(90) |
it can harden further by three-body interactions in which a passing star
is captured and then ejected at high velocity. The timescale, a /
, for hardening in this
regime is
 |
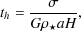(91) |
where the dimensionless hardening rate H
15. If hardening
continues long enough, the binary eventually becomes sufficiently hard
that gravitational radiation dominates the evolution of the system which
then coalesces on a timescale of
(Peters 1964)
 |
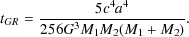(92) |
The fly in the ointment of this neat picture is that the above estimates for the rate of hardening by stellar encounters assumes a fixed stellar background. In reality, as stars are ejected in three-body encounters the parts of phase-space containing stars that can be captured becomes depleted (so-called "loss cone depletion"). This inevitably slows the hardening process. The past ten years have seen numerous studies of this process and examination of various mechanisms by which the loss cone may be refilled. For example, Yu (2002) finds that in triaxial potentials scattering of stars can efficiently refill the loss cone while Gould and Rix (2000) suggest that the presence of a gaseous disk surrounding the black holes can help harden the binary. Numerical and analytical works have also indicated that the random walking of the binary center of mass may help mitigate loss cone depletion (Quinlan and Hernquist 1997; Milosavljevic and Merritt 2001), while the effective refilling of the loss cone by ejected stars returning on eccentric orbits (Milosavljevic and Merritt 2003; Sesana et al. 2007) and interactions with stars bound to the binary (Sesana et al. 2008) may enhance the rate of hardening. While the details remain uncertain it seems that this basic process can lead to black holes merging in less than 10 Gyr.
In addition to their mass, cosmological black holes are characterized by one other parameter, their angular momentum 25. The spin of a black hole can have a strong influence on the radiative efficiency and jet power of black holes (see Section 6.3.2) and so the cosmological evolution of this quantity is important to understand. There are fundamentally two mechanisms which change the spin of a black hole: merging with another hole and accretion of material.
The outcomes of binary black hole mergers have proven very difficult to simulate numerically. However, recent advances in numerical techniques have allowed for successful simulation of the entire merging process (e.g. Tichy and Marronetti 2007) and, therefore, determination of the final spin of the merger product. While the number of simulations carried out to date is small, Boyle et al. (2008) exploit symmetries of the problem to construct simple fitting formula which accurately predict the spin of the final black hole as a function of the incoming black hole masses, spins and orbital properties.
As first considered by Bardeen (1970), material accreted from an accretion disk carries with it some angular momentum (approximately equal to its angular momentum at the latest stable circular orbit, before it began its plunge into the black hole). Defining a dimensionless spin parameter for a black hole through
 |
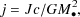(93) |
where J is the angular momentum of the hole of mass
M,
such that 0
j 1, then
Shapiro
(2005)
defines a dimensionless spin-up function s(j) by
 |
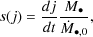(94) |
where 
, 0 is the rate of
rest mass accretion. For a standard,
relativistic, Keplerian thin disk accretion flow with no magnetic
fields, the expected spin-up function due to accretion is given by
(Shapiro
2005)
 |
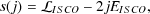(95) |
where
 |
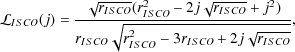(96) |
and
 |
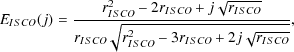(97) |
are the (dimensionless) specific angular momentum and specific energy of
the innermost stable circular orbit (ISCO) of the black hole
respectively. The radius of the ISCO orbit (in units of the
gravitational radius G
M /
c2) is
 |
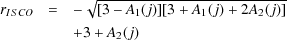(98) |
where
 |
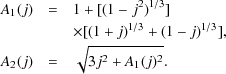(99) (100) |
Thorne (1974)
found a small correction to this formula due to the fact that the hole
preferentially swallows negative angular momentum photons resulting in a
spin-up function for the standard thin disk that is positive for all
j < 0.998, and therefore lets the black hole spin up to
j 0.998 in
finite time as noted by
Shapiro
(2005).
For a thick accretion flow the result is somewhat different (since the
flow is no longer supported against gravity by its rotation alone as it
has significant thermal and magnetic pressure).
Benson
and Babul (2009)
compute the spin-up function for ADAF models. Additionally,
Benson
and Babul (2009)
compute how the magnetic torques which allow black holes to drive jets
(via the Blandford-Znajek and/or Blandford-Payne mechanisms;
Blandford and Znajek 1977,
Blandford and Payne 1982)
result in a braking torque on the black hole, spinning it down and
resulting in an equilibrium spin of j
0.93 for a hole
accreting from an ADAF.
The relative importance of mergers and accretion for determining the spins of cosmological black holes depends upon the rate of galaxy mergers, the supply of gas to the black hole and additional factors such as the alignment of accretion disks and black hole spins and merging black hole spins and orbits. Many of these factors are not too well understood. However, cosmological calculations (Berti and Volonteri 2008; see also Volonteri et al. 2005) suggest that accretion dominates over mergers in terms of determining the spins of supermassive black holes, with the consequence that most such holes are predicted to be rapidly spinning.
One additional consequence of black hole mergers is that the gravitational waves emitted during the final inspiral carry away linear momentum resulting in the black hole recoiling in the opposite direction with a velocity potentially large enough to unbind it from the galaxy (Fitchett 1983; Favata et al. 2004; Merritt et al. 2004; Blanchet et al. 2005). Studies of this effect within a cosmological framework suggest that such ejected black holes (wandering through intergalactic space) can make up 2-3% of the total mass density of supermassive black holes, while in individual cases they can account for up to half of the total black hole mass associated with a galaxy (Libeskind et al. 2006).
As early as 1974 (Larson 1974; see also White and Rees 1978; Dekel and Silk 1986) it was realized that star formation could not proceed with 100% efficiency in all dark matter halos. Evidence for this comes from multiple observed facts, but the two crucial ones are:
*
= (2.3 ± 0.34) × 10-3
(Cole et
al. 2001),
much less than the total baryonic mass density of the Universe
b =
0.0462 ± 0.0015
(Dunkley et al. 2009).
Therefore, only a small fraction of all baryons have been able to turn
into stars.
This second point can be made even stronger: if all dark matter halos turned a constant fraction of their mass into stars we would still have too many faint relative to bright galaxies. There are a wealth of other observational constraints which indicate that the efficiency of galaxy formation must depend strongly upon halo mass - a useful summary of these constraints is given by Behroozi et al. (2010).
Clearly what is needed is some process which preferentially suppresses the formation of stars in lower mass dark matter halos. The usual suspect for this process is energy/momentum input from supernovae explosions, perhaps augmented by stellar winds.
A similar problem occurs in the most massive dark matter halos. Although cooling is relatively inefficient in such halos they can nevertheless cool significant mass of gas over cosmic time. Unchecked, this leads to the formation of galaxies significantly more luminous than any that are observed. The energetic requirements of this problem suggest that AGN are a possible solution.
6.3.1. Supernovae/Stellar Winds
Energy input from SNe due to a single stellar population are shown in
Fig. 10. If we assume that a fraction
of this energy is
coupled into an outflow of ISM gas which leaves the galaxy at the escape
velocity (so that we do not waste energy by giving the gas a velocity at
infinity) this results in an outflow rate
out given
by
 |
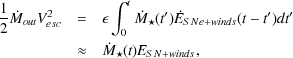(101) |
where in the last step we have approximated energy input from SNe and winds as occurring instantaneously after star formation. This implies an outflow rate of
 |
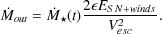(102) |
This has the required features: given some initial mass of cold gas, a
fraction 1 / (1 +
) where
2
ESN+winds / Vesc2 will be
turned into stars, resulting in much lower star formation efficiencies
in low mass galaxies.
Figure 10 shows the cumulative energy input
26 into the interstellar
medium as a function of time from a
1 M
burst of star formation with a
Chabrier (2003)
initial mass function.
 |
 |
Figure 10. Cumulative energy input into the interstellar medium, expressed as the number of equivalent supernovae, per unit mass of stars formed as a function of time for a Chabrier initial mass function. The two panels show results for two different metallicities as indicated in the panels. The long dashed line indicates the contribution from stellar winds, the dotted line the contribution from Type Ia supernovae and the short dashed line the contribution from Type II supernovae. The solid line shows the sum total of all contributions. |
|
Similar arguments can be made using the momentum of supernovae explosions to drive the wind, which may be more relevant if energy is efficiently radiated from expanding SNe bubbles 27 (Murray et al. 2005). The rate of momentum injection from supernovae is given by (Murray et al. 2005)
 |
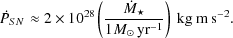(103) |
Since the momentum in any wind driven by this momentum input must
satisfy
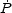W =
out
V
, where
V is
the wind velocity at infinity we have that
 |
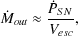(104) |
where we have assumed that
V
Vesc
(Murray
et al. 2005).
This gives a different scaling with the galaxy escape velocity compared
to energy driven winds.
The details of how supernovae feedback actually operates remain somewhat unclear, and is complicated by the necessity to understand how an expanding supernovae remnant interacts with a complex, multiphase interstellar medium. Our discussion below will mostly follow Efstathiou (2000; see also McKee and Ostriker 1977).
The basic picture considered involves a two phase interstellar medium consisting of hot, diffuse material (which fills most of the volume) and cold, dense clouds (which contain most of the mass). Evaporation of cold clouds by supernovae moves gas from the cold phase into the hot phase. Outflows, and suppression of star formation, from the hot phase will result if the hot phase:
The effectiveness of feedback in such a model can be examined by considering the mass of cold clouds swept up and evaporated by an expanding supernovae remnant, Mev. Efstathiou (2000) finds
 |
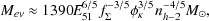(105) |
where E51 is the energy released by a supernovae in units of 1051 ergs, nh-2 is the number density of hydrogen in units of 10-2 cm-3, and the evaporation parameter as defined by McKee and Ostriker (1977) is
 |
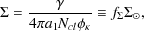(106) |
where 
=
vh / ch
2.5 relates the blast
wave velocity, vh, to the isothermal sound speed,
ch, a1 is a typical cloud radius,
Ncl is the number of clouds per unit volume,
relates the effective conductivity,
eff, to the
classical thermal conductivity,
,
via eff =
and
95 pc2 is
the value of the evaporation parameter in the Solar neighborhood. (Units
are chosen so that all variables have values of order unity in a typical
galaxy.)
Since Mev is significantly larger than the mass of stars formed per supernovae then we may expect that if a significant fraction of this evaporated gas can escape as a wind then star formation may be efficiently suppressed.
Gas in the hot phase will escape the galaxy if its specific enthalpy
 |
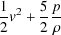(107) |
exceeds its specific gravitational binding energy. This therefore requires that we determine the thermodynamic properties of the hot phase. Efstathiou (2000) does this by assuming that supernovae remnants have a porosity of unity (i.e. the total volume of remnants equals the volume of the galaxy, thereby creating an overlapping network of remnants). Given a model for the expanding supernovae remnant this allows the thermodynamic properties of the hot phase to be determined.
Efstathiou (2000) shows that such a model of feedback can indeed produce self-regulated star formation in a galaxy disk that is quiescently forming stars (bursts are not required) and that both negative and positive (due to pressure-enhanced star formation) feedback can work simultaneously.
Very simple energetic arguments suggest that the energy output involved in building a black hole in a galaxy can have significant effects on the formation of the galaxy itself (Benson et al. 2003). To order of magnitude, let us assume that each galaxy contains a supermassive black hole with a mass equal to 0.1% of its stellar mass. The energy released by the formation of the black hole per unit mass of stars formed is then
 |
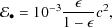(108) |
where is the
efficiency of conversion of rest mass into energy output (either in
radiation or mechanical outflow). For typical values of
~ 0.1 this implies
= 1.8 ×
1050 ergs
M-1, which is an order of magnitude greater
than that released by supernova explosions and stellar winds and is
comparable to the energy released by cooling gas in forming some of the
most massive galaxies.
Feedback from AGN has the potential to directly link the properties of
supermassive black holes and their host galaxies. As such, it may be a
natural explanation for the observed correlations between supermassive
black hole mass and galaxy mass or velocity dispersion. The first study
of how AGN feedback can lead to such correlations
28 was described by
Silk and
Rees (1998).
They showed that, on quite general grounds, coupling of the energy
released by the formation of the supermassive black hole to the
surrounding forming galaxy would lead to a relationship close to the
observed
M -
relation. The
generality of these arguments imply that this result may be reasonably
independent of the details of any more specific feedback model.
The physical mechanism through which AGN feedback operates remains somewhat unclear. AGN likely radiatively heat cooling gas in the atmosphere surrounding galaxies, reducing the rate at which that gas can cool. Additionally, radiatively driven winds originating from the broad line region surrounding the black hole may result in mechanical feedback on the galaxy itself. Finally, in low accretion states, AGN may drive highly collimated and powerful jets which can reach out well into the surrounding halo. Plausibly all of these mechanisms could be active during galaxy formation.
Ciotti et al. (2009) examined the roles of radiative and mechanical feedback modes. They find that radiative feedback alone, while able to forestall the "cooling catastrophe" (see Section 8.3), is unable to sufficiently limit the growth of black holes, resulting in them being too massive for a given galaxy (by a factor of around four). Mechanical feedback is found to be successful in limiting the growth of black holes. This is in agreement with other numerical simulations, such as Springel et al. (2005a), Matteo et al. (2005), Sijacki et al. (2007), Sijacki et al. (2009), Booth and Schaye (2009), which incorporate energy injection from quasars (typically triggered by major mergers) and show that AGN activity can effectively expel gas from a galaxy and can establish the observed correlations between supermassive black hole and galaxy properties. However, Ciotti et al. (2009) find that mechanical feedback of high efficiency (as is required to match the scaling relations) is too effective, depleting galaxies of gas to a degree greater than is observed, while low efficiency mechanical feedback allows too much star formation to occur at late times, resulting in blue cores in elliptical galaxies that are inconsistent with observations. Precisely how efficiently jets from an AGN can couple their energy to the surrounding hot gas remains a topic of intense study. The general picture that is emerging is that the jets inflate bubbles or cavities in the hot atmosphere. For example, Omma et al. (2004) use numerical simulations to show that jets inflate cavities in the hot gas that can excite g modes in the cluster atmosphere and heat the gas, while Roychowdhury et al. (2004) explore a model in which the bubbles are buoyant and heat the atmosphere by doing pdV work as they rise.
Recent years have seen numerous implementations of detailed models of
galaxy formation incorporating AGN feedback
(Scannapieco and Oh 2004;
Croton et
al. 2006;
Bower et al. 2006;
Cattaneo et al. 2006;
Somerville et al. 2008b).
These have shown that AGN feedback can explain the long standing issue
of the exponential break in the galaxy luminosity function (without AGN
feedback such models tend to produce far too many bright galaxies;
Benson et
al. 2003)
and helps produce a bimodal distribution of galaxy colors (as AGN
feedback makes massive galaxies "red and dead"). These models typically
assume a "radio mode" feedback in which the AGN drives jets out of the
galaxy while in a radiatively quiet state.
Benson
and Babul (2009)
give an expression for the jet power produced by a spinning black hole
accreting from a geometrically thick accretion flow
29 relevant to this
situation. As a result this type of AGN feedback is effective only when
there is a quasi-hydrostatic atmosphere of hot gas in a dark matter halo
for it to couple to. Therefore, AGN feedback only works in the virial
shocking regime, resulting in it being important above a critical halo
mass of order 1012
M (with
a weak redshift dependence).
The first generation of stars (known as Population III) and galaxies must have formed from primordial gas which is (almost) metal free. Stellar nucleosynthesis and subsequent pollution of the ISM and IGM (through stellar winds and supernovae explosions) with heavy elements has a significant impact on later generations of galaxies. In particular, the presence of heavy elements significantly alters the rate at which gas can cool (see Section 3.2) and leads to the formation of dust which both attenuates optical and UV light from galaxies and re-emits that light at longer wavelengths. To accurately model the properties of galaxies therefore requires a treatment of chemical enrichment.
The fraction of material returned to the ISM by a stellar population as a function of time is given by
 |
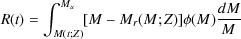(109) |
where (M) is the initial mass function normalized to unit
stellar mass and Mr(M) is the remnant mass of a
star of initial mass M. Here, M(t) is the mass of a
star with lifetime t. Figure 11 shows
the fraction of material recycled to the interstellar medium from a
single stellar population as a function of time, t, since the
birth of that population. Typical Pop. II initial mass functions (e.g.
Salpeter 1955,
Chabrier 2003)
lead to around 40% of mass being recycled after 10 Gyr, dropping to
around 30% at 1 Gyr. A Pop. III initial mass function recycles much more
mass (since it consists of much more massive stars), recycling 70% of
the mass within a few tens of millions of years.
 |
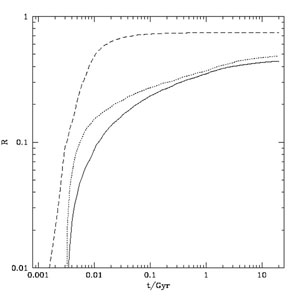Figure 11. The fraction of mass from a single stellar population born at time, t = 0, recycled to the interstellar medium after time t. Solid and dotted lines show results for a Chabrier initial mass function with zero and Solar metallicity respectively, while the dashed line shows results for zero metallicity (Pop. III) stars with a lognormal IMF (case A from Tumlinson 2006). |
 |
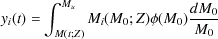(110) |
where Mi(M0; Z) is the mass of metals produced by stars of initial mass M0. For a specified IMF we can compute yi(t; Z) for all times and elements of interest. Figure 12 shows examples of the total metal yield for Pop. II and Pop. III initial mass functions. Typical total metal yields for Pop. II are around 0.04 increasing to 0.1 for the Pop. III initial mass function shown here. Stellar data are taken from Portinari et al. (1998) for low and intermediate mass stars and Marigo (2001) for high mass stars.
 |
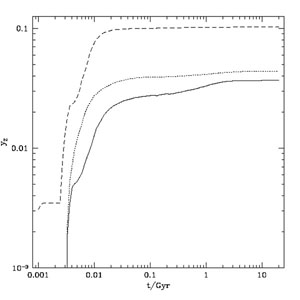Figure 12. The total metal yield from a single stellar population born at time, t = 0, after time t. Solid and dotted lines show results for a Chabrier initial mass function with zero and Solar metallicity respectively, while the dashed line shows results for zero metallicity (Pop. III) stars with a lognormal IMF (case A from Tumlinson 2006). |
In many cases, the process of chemical enrichment has been simplified by adopting the instantaneous recycling approximation, in which mass and metals are assumed to be returned to the interstellar medium instantaneously after the formation of a population of stars (essentially assuming that stellar evolution happens instantaneously). Typically, the recycled fractions and yields are evaluated at some time, t, of order the age of the Universe. This approximation is reasonable at late times, when the ages of typical stellar populations in galaxies is several Gyr. For example, Fig. 12 shows that the metal yield is approximately constant after about 0.1 Gyr, although the recycled fraction (see Fig. 11) does not converge so rapidly. The advantage of the instantaneous recycling approximation is that it greatly simplifies the equations governing chemical enrichment such that we have
 |
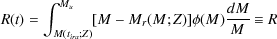(111) |
with a similar result for yields. The normal convolution integral to determine the rate of return of mass to the interstellar medium,
 |
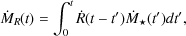(112) |
then simplifies to
 |
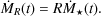(113) |
This removes the need for knowledge of the entire star formation history of a galaxy to determine the rate of recycling (which can greatly reduce computational demand in numerical models of galaxy formation).
While the instantaneous recycling approximation has its advantages, it
is, of course, an approximation and one which breaks down in regimes of
rapid star formation and at high redshifts where stars are much less
than 10 Gyr old (since the Universe itself is very young). Detailed
models of chemical evolution are well established within the monolithic
collapse scenario
(Matteucci and Greggio 1986;
Matteucci and Gibson 1995;
Timmes
et al. 1995;
François et al. 2004;
Pipino and Matteucci 2004,
2006;
Romano et al. 2005),
but have only received limited study within the physically motivated
context of hierarchical galaxy formation. Numerous hydrodynamical
simulation codes now contain implementations of chemical enrichment
(Scannapieco et al. 2005;
Kobayashi et al. 2007;
Pontzen
et al. 2008;
Gnedin
et al. 2009).
Semi-analytic models of galaxy formation are beginning
30 to implement detailed
chemical enrichment models also
(Nagashima et al. 2005a,
b;
Pipino et
al. 2008;
Arrigoni et al. 2009).
Within the context of hierarchical structure formation models such
chemical enrichment modeling has been shown to be in agreement with
measurements of the intracluster medium metallicities of individual
elements
(Nagashima et al. 2005a),
to reproduce the observed trend of metallicity and
[
/Fe] with stellar mass
in elliptical galaxies
(Arrigoni et al. 2009)
and to reproduce the measured distribution of metallicities in damped
Lyman- systems
(Pontzen
et al. 2008).
Observational studies of galaxies make use of radiation emitted by them (or, sometimes, the lack of radiation due to absorption by galaxies) to infer their physical properties. As such, it is often crucial to be able to compute the emergent spectrum from each galaxy in a theoretical model. This is two-step process, involving first computing the spectrum of light emitted by all of the stars (and possibly the AGN) in the galaxy and, secondly, computing how this light is reprocessed by the gas and dust in the galaxy and along the line of sight from the galaxy to the observer.
6.5.1. Steller Population Synthesis
In the absence of absorbing dust or gas, the luminosity as a function of
frequency for a galaxy, the spectral energy distribution (SED), is
simply a sum over the SEDs of its constituent stars. We can imagine a
galaxy as consisting of numerous "simple stellar populations" -
populations of stars of the same age, metallicity and initial mass
function. The luminosity,
L
(galaxy), of a galaxy at
frequency is then simply
given by the following convolution integral
 |
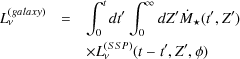(114) |
where *(t, Z) is the rate of
formation of stars of metallicity Z in the galaxy at time
t and L(SSP)(t, Z,
) is the
luminosity of a simple stellar population of age t, metallicity
Z and with initial mass function
(M).
Given a model which predicts the rate of star formation in a galaxy as a
function of time and metallicity (which is the galaxy formation aspect
of this calculation), the problem is reduced to determining suitable
L(SSP) (the stellar astrophysics
aspect of the calculation). This, in turn depends upon the spectra of
individual stars,
L(star)(t, Z), and
the stellar initial mass function,
(M),
such that
 |
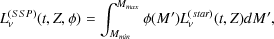(115) |
where Mmin and Mmax are the minimum and maximum masses for stars respectively.
Several libraries exist which provide
L(SSP)(t, Z,
) for several
different ages, metallicities and initial mass functions
(Bruzual
and Charlot 2003;
Maraston 2005;
Dotter et
al. 2007;
Conroy et al. 2008;
Lee et
al. 2009).
These are constructed using a combination of theoretical stellar
evolution models, observations of stars of known age and metallicity and
theoretical models of stellar atmospheres where no good observations
exist. While enormous progress has been made in understanding the
spectra of stars significant uncertainties remain. For example,
Conroy et al. (2008),
who performed a study of how uncertainties in such models propagate into
constraints derived from galaxy observations, find that current models
do not fully characterize the metallicity dependence of the thermally
pulsating asymptotic giant branch phase and that uncertainties in the
slope of the initial mass function
31 lead to an uncertainty
in the evolution of the K-band magnitude of a stellar population of
around 0.4 magnitudes per unit redshift (which leads to significant
uncertainty when trying to interpret or predict the evolution of galaxy
populations).
6.5.2. Dust Absorption and Re-emission
The presence of dust in galaxies has been known for a long time, and the effects of this dust on the observed properties of galaxies have been extensively studied. Simply put, dust absorbs light emitted by stars (and AGN), particularly at short wavelengths, is heated by this light and therefore re-emits it at longer wavelengths (typically in the infrared and sub-mm). The presence of dust in galaxies can therefore significantly affect their observed luminosities at optical and UV wavelengths. Models of galaxy formation must therefore take into account the effects of dust before comparing their predictions to observational data. The simplest such approach, adopted by many early models, is a "obscuring screen" or "slab" geometry, in which a plane of dust is placed in front of the model galaxy, given an extinction curve measured from the Milky Way (for example) and normalized to have an optical depth at optical wavelengths based on properties of the model galaxy (gas content and metallicity). This provides a simple estimate of the amount of extinction, but clearly does not reflect the true geometry of the dust (which is distributed throughout the galaxy) or the fact that stars may preferentially form in dense, dust regions.
Cole et al. (2000) introduced a model for dust extinction in galaxies which significantly improved upon earlier "slab" models. In Cole et al. (2000) the mass of dust is assumed to be proportional to the mass and metallicity of the ISM and to be mixed homogeneously with the ISM (possibly with a different scale height from the stars) and to have properties consistent with the extinction law observed in the Milky Way. To compute the extinction of any galaxy, a random inclination angle is selected and the extinction computed using the results of radiative transfer calculations carried out by Ferrara et al. (1999).
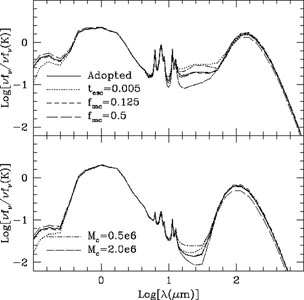
Beyond these relatively simple models of dust extinction it has recently become possible to employ much more realistic ray tracing techniques to compute the effects of dust on galaxy spectra. For example, the Grasil software (Silva et al. 1998) is designed to compute the radiative transfer of star light through an idealized galactic geometry consisting of a disk and a bulge each of which may contain both diffuse and clumpy gas and dust. Grasil takes an input galactic SED together with physical parameters of a galaxy (size of each component, metallicity and mass of gas present) and computes the resulting SED including absorption, scattering and remission from the dust, taking into account a realistic distribution of grains and polycyclic aromatic hydrocarbons (PAHs) the temperature distribution of which are computed self-consistently, and assuming that stars are born in the dense molecular clouds and escape from these on some timescale (leading to enhanced absorption in the UV which is produced primarily by young stars) (Fig. 13). This code is therefore ideal for (semi-)analytic studies of galaxies and has been employed to examine the expected properties of submillimeter and infrared galaxies in hierarchical cosmologies (Granato et al. 2000; Baugh et al. 2004, 2005; Lacey et al. 2008; Swinbank et al. 2008).
Similarly, the Sunrise code of Jonsson (2006) and Radishe by Chakrabarti and Whitney (2009) solve essentially the same problem (radiative transfer through a dusty medium) but work for arbitrary geometry using Monte Carlo, polychromatic algorithms and so are particularly well suited to hydrodynamical simulations of galaxy formation, allowing realistic images of simulated galaxies to be made at any wavelength. Sunrise has been applied to studies of luminous infrared galaxies (Younger et al. 2009), quantitative morphology of merger remnants (Lotz et al. 2008), physical models to infer star formation rates from molecular indicators (Narayanan et al. 2010) and tests of our ability to recover physical parameters of galaxies from their broadband SEDs (Wuyts et al. 2009).
 |
 |
Figure 13. Left-hand panel: An example of the spectral energy distributions from two face-on spiral galaxies as computed by Grasil (Granato et al. 2000). The SED shows direct emission from stars at short wavelengths, with reprocessed light emitted from dust at long wavelengths. In the intermediate region lines associated with PAHs are visible. Reproduced, with permission, from Granato et al. (2000). Right-hand panel: An image of a post-merger galaxy from a simulation by Cox et al. (2008) as computed by Sunrise (Jonsson 2006). A complex dust morphology, including a strong dust lane, is clearly visible. Reproduced, with permission, from Cox et al. (2008). |
|
Since these ray tracing methods are computationally expensive they
cannot yet be applied to large samples of model galaxies. Therefore,
attempts have been made to construct simpler algorithms which capture
most of their results. For example,
Gonzalez-Perez et al. (2008)
extended the model of
Cole
et al. (2000)
by assuming that some fraction, fcloud, of the dust is
in the form of dense molecular clouds where the stars form (see
Baugh et
al. 2005).
Stars were assumed to form in these clouds and to escape on a timescale
of 
quies (for
quiescent star formation in disks) or
burst (for star
formation in bursts), which is a parameter of the dust model
(Granato et al. 2000).
Since massive, short-lived stars dominate the UV emission of a galaxy
this enhances the extinction at short wavelengths, so these stars spend
a significant fraction of their lifetime inside the clouds.
To compute emission from dust they assumed a far infrared opacity of
 |
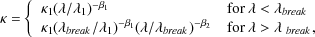(116) |
where the opacity normalization at
1 = 30
µm is chosen to be
1 = 140
cm2/g to reproduce the dust opacity model used in
Grasil, as described in
Silva et al. (1998).
The dust grain
model in Grasil is a
slightly modified version of that proposed by
Draine
and Lee (1984).
Both the
Draine
and Lee (1984)
and Grasil dust models have
been adjusted to fit data on dust extinction and emission in the local
ISM (with much more extensive ISM dust emission data being used by
Silva et al. 1998).
The normalization is set at 30µm because the dust opacity in
the
Draine
and Lee (1984)
and Grasil
models is well fit by a power-law longwards of that wavelength, but not
shortwards. The dust luminosity is then assumed to be
 |
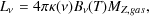(117) |
where
B(T) =
[2h3 /
c2] /
[exp(h /
kT) - 1] is the Planck blackbody spectrum and
MZ,gas is the mass of metals in gas. The dust
temperature, T, is chosen such that the bolometric dust
luminosity equals the luminosity absorbed by dust.
This extended dust model, including diffuse and molecular cloud dust components, provides a better match to the detailed results of Grasil while being orders of magnitude faster, although it does not capture details such as PAH features.
Fontanot et al. (2009b) have explored similar models which aim to reproduce the results of Grasil using simple, analytic prescriptions. They found that by fitting the results from Grasil they were able to obtain a better match to the extinction in galaxies than previous, simplistic models of dust extinction had been able to attain.
6.6. Absorption by the Intergalactic Medium
In addition to having to pass through the internal gas and dust in each
galaxy, light emitted from a galaxy must pass through the entire
intervening intergalactic medium between it and ourselves before we can
observe it. The intergalactic medium contains significant amounts of
neutral hydrogen (even at relatively low redshifts, long after
reionization) which is known to be clumped into clouds by virtue of
observations of the
Lyman- forest of
absorption systems in quasar spectra. Light emitted at redshift
zem at some wavelength
em,
shortwards of the
Lyman- wavelength of
1216 Å, will eventually be redshifted into the
Lyman- line and so will
be absorbed by any clouds of neutral hydrogen at redshift 1 +
zabs = (1 + zem)
[em / 1216
Å]. Light emitted at even shorter
wavelengths may be additionally absorbed by higher lines in the Lyman
series, or by the Lyman continuum shortwards of 912 Å.
Models of the effective optical depth due to this absorption (based upon
the observed distribution of
Lyman- forest absorber
properties) have been described by
Madau
(1995)
and
Meiksin
(2006).
The resulting absorption of starlight shortwards of
Lyman- is so severe that
galaxies appear essentially dark at wavelengths shorter than
obs = 1216
Å (1 + zem). This
forms the basis of the "dropout" techniques for identifying high
redshift galaxies and quasars on the basis of their broadband colors
(Madau et al. 1996;
Fan et
al. 2001).
24 http://lisa.nasa.gov/ Back.
25 They will not possess any significant charge, as this would be quickly neutralized by accretion of oppositely charged material. Back.
26 We assume that a Type II supernovae releases 1051 ergs of usable energy. We express the energy input in units of 1051ergs so that it can be interpreted as the equivalent number of supernovae. Back.
27 The momentum, of course, cannot be radiated away. Back.
28 Once again, assuming that any causative process is needed at all (Jahnke and Maccio 2010). Back.
29 The jet power from a hole accreting from a thin accretion disk is much lower, due to the much weaker magnetic field in such a disk. Back.
30 Implementation of chemical enrichment models of this type is, in many ways, significantly easier in N-body simulations than in semi-analytic models. N-body simulations that include star formation typically spawn new star particles during each timestep to represent the stars formed at that time. Each particle can therefore be trivially tagged with a formation time and metallicity. On subsequent timesteps the rate of mass and metal return from that particle is easily computed and applied to surrounding gas particles for example. Semi-analytic models on the other hand have traditionally not recorded the full star formation history of each galaxy (due to computational resource requirements) as is needed to compute the chemical enrichment at each timestep. This can, of course, be done, as we are now seeing. Back.
31 See Kroupa (2001) for a recent discussion of the difficulties associated with determining the local initial mass function. Kroupa (2001), along with Chary (2008) and van Dokkum (2008), also discuss evidence for the non-universality of the initial mass function, although no definitive evidence for such yet exists. Back.