Having reviewed the major inputs to our current theory of galaxy formation and explored some of the tools employed to solve them, in this section we briefly explore five topics of particular interest in contemporary galaxy formation theory.
After the initial excitement of the Big Bang, inflation, nucleosynthesis
and the recombination the Universe enters a protracted period of
relative quiescence, known as the "Dark Ages", during which there are no
luminous sources and structure grows primarily only in the dark
sector. The end of the Dark Ages is thought to occur when the first star
forms. The formation of these first stars is an unusual problem in
astrophysics in that it represents a clean, well-defined problem that
can be tackled numerically - the initial conditions are simply those of
an expanding Universe containing small perturbations in the dark matter
and baryonic components which is a simple mixture of hydrogen and
helium. As such, this problem has been examined and explored in
significant detail
(Abel et
al. 2002;
Yoshida et al. 2006;
Gao et
al. 2007).
The consensus picture that has emerged from this work is that the first
star will form due to gas collapse and cooling (via the gas-phase
formation of molecular hydrogen) in a halo of mass around 106
M
at a
redshift of z
50. The first star is
likely to be very massive (current simulations cannot follow the
evolution of the proto-star beyond the point at which it becomes
optically thick in various lines of molecular hydrogen due to a lack of
treatment of the necessary radiative transfer, but at this stage the
collapsing core typically has an accretion rate that is expected to lead
to the formation of a star with a mass of several tens of Solar masses)
and, therefore, short lived. What happens after this first star forms
rapidly becomes a much more complicated problem, involving the poorly
understood physics of supernovae explosions and the numerically
challenging problem of radiative transfer.
Needless to say then, studying the formation of the first galaxies is more complicated still, although no more complicated than modeling the formation of later generations. In the next decade new facilities such as JWST and thirty meter class telescopes will begin to open a window on the earliest generations of galaxies and, as such, there is a need for theoretical understanding and predictions for this epoch of cosmic history. In particular, this represents a real opportunity to make testable predictions from galaxy formation theory which can be confronted with data in the near future.
In considering the earliest generations of galaxies there are various physical processes which, while often neglected at lower redshifts, are of potentially crucial importance. For example, understanding the properties of Population III stars, their various feedback processes (both positive and negative) and initial mass function (Glover and Abel 2008; Trenti and Stiavelli 2009; Ohkubo et al. 2009; Machida et al. 2008; Lawlor et al. 2008; O'Shea and Norman 2007, 2008; Harris et al. 2007; Stacy and Bromm 2007) may be crucial for understanding how this population of galaxies grows (Tegmark et al. 1997; Ricotti et al. 2001; Wise and Abel 2007a, b; Greif et al. 2008; Wise and Abel 2008b; Wise et al. 2008; Bromm et al. 2009). Additionally, connecting these galaxies to later generations involves understanding how they evolve through (and cause) the epoch of cosmic reionization (Benson et al. 2002a; Alvarez et al. 2008), modeling non-local feedbacks (i.e. interactions between neighboring galaxies or the galaxy population as a while) and feedbacks in general (Busha et al. 2009).
Various interesting questions await definitive answers. For example, how
long is the period of Population III star formation? This seemingly
simple question depends on how we define Population III - theoretical
reasoning suggests that we may expect a significant shift in the initial
mass function once gas is raised above a critical metallicity of
10-4
Z
(Santoro and Shull 2006)
and the ability of Population III stars to enrich their surroundings
(and, therefore, future generations of star formation). Since Population
III stars are likely to produce many more hydrogen ionizing photons per
unit mass than their Population II counterparts this question may have
important consequences for the reionization history of the Universe.
Reionization itself remains an interesting problem. While it has been convincingly demonstrated theoretically (Chiu and Ostriker 2000; Ciardi et al. 2003; Somerville et al. 2003; Benson et al. 2006) that the universe could be reionized by galaxies sufficiently early to match constraints on the optical depth to the CMB (Dunkley et al. 2009) these calculations are currently forced to make assumptions about the distribution of mass and ionized regions in the IGM and about the ionizing photon escape probability from high redshift galaxies (Dove et al. 2000; Ricotti and Shull 2000; Razoumov and Sommer-Larsen 2006; Gnedin et al. 2008; Yajima et al. 2009; Wise and Cen 2009) which are still poorly understood.
In addition to observing high redshift galaxies directly, it may be possible to learn much about them from the study of their present day remnants. "Galactic archeology" of this sort has been investigated quite extensively (Freeman and Bland-Hawthorn 2002; Scannapieco et al. 2006b; Brook et al. 2007).
The conclusions are that Population III stars (usually taken as a
convenient proxy for "first galaxies") that formed in progenitor
galaxies of the Milky Way likely formed over a fairly broad range of
redshifts, with the formation rate peaking at z
10 but continuing
until z
4-5 (in chemically
isolated halos which have not been contaminated by metals produced by
star formation in earlier forming halos). As such, any remnants of these
stars are probably spread over most of the nearby Galactic halo. The
lack of detection of such metal-free stars therefore places constraints
on their initial mass function - they must have been sufficiently
massive to have evolved off of the main sequence by the present
day. Currently, this suggests that such stars must have been more
massive then about 0.8
M
(Brook et
al. 2007).
If we examine truly old stars, however, the situation is rather
different. Simulations suggest that these formed in halos close to the
high density peak that eventually formed the final system, and therefore
are preferentially located in the central regions (typically the bulge)
of the Milky Way.
8.2. The Formation and Sizes of Galaxy Disks
Galactic disks are, perhaps, the most prominent feature of galaxies in the local Universe. Additionally, recent observations (Law et al. 2009; Schreiber et al. 2009) have demonstrated that massive disks are already in place as long ago as z = 2. Understanding the details of how disks form and grow is therefore of crucial importance for galaxy formation theory (Silk 2001).
The basic picture has been in place for a long time (Fall and Efstathiou 1980). Collapsing systems of dark matter and gas are imparted some small amount of angular momentum as a result of tidal torques from inhomogeneities in the surrounding matter distribution (Hoyle 1949; Barnes and Efstathiou 1987). While gas can radiate energy and thereby collapse to form a galaxy it cannot radiate angular momentum. As such, angular momentum is conserved 33 during the collapse and is eventually responsible for halting that collapse when the proto-galaxy reaches a radius at which its angular momentum is sufficient to provide support against the gravitational potential in which it resides. Back of the envelope type estimates of the resulting sizes of disks show that this picture produces disks with sizes comparable to those that are observed (Fall and Efstathiou 1980; Mo et al. 1998). However, this basic picture makes several simplifying assumptions, some of them difficult to justify. A careful analysis of these assumptions is therefore warranted to understand the process of disk formation in greater detail.
It has been convincingly established that the distribution of angular momentum of gas in halos prior to any cooling and galaxy formation is similar to that of the dark matter (van den Bosch et al. 2002, 2003) in so far as the distribution of spin parameters is very similar (the directions of the angular momenta vectors of dark matter and gas are often misaligned; van den Bosch et al. 2002). The distribution of the angular momentum of gas within an individual halo is less well studied, but recent hydrodynamical simulations (Sharma and Steinmetz 2005) have demonstrated that the distribution of the specific angular momentum, j, can be well described by a simple form:
 |
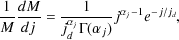(118) |
where 
is the gamma
function, M is the total mass of gas,
jd = jtot /
and
jtot is the mean specific angular momentum of the
gas. The parameter
j takes on
different values in different halos, with a median value of 0.89. The
fraction of mass with specific angular momentum less than j is
then given by
 |
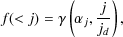(119) |
where 
is the incomplete gamma function. Despite this knowledge
of the initial distribution of angular momentum in the baryonic
component, the question of how well angular momentum is conserved during
the process of cooling and collapse is less clear. However, recent
simulation studies have begun to shed some light on this issue.
Zavala et
al. (2008)
describe high resolution SPH simulations in which the baryonic physics
(particularly the star formation and feedback from supernovae) is varied
such that one simulation results in the formation of a disk galaxy and
another in the formation of a spheroidal galaxy. They show that, in the
case of the disk galaxy the angular momentum of the baryonic material
that will eventually form the galaxy tracks the behavior of the dark
matter angular momentum: growing as predicted by linear theory at early
times and then remaining constant. In the case of the spheroidal galaxy,
the angular momentum still grows initially as expected from linear
theory, but then 90% is rapidly lost as pre-galactic fragments undergo
mergers which transfer their angular momentum to the dark matter. In the
disk galaxy case, strong feedback prevents gas from cooling into these
small halos at early times, and so avoids angular momentum loss to the
dark halo.
In addition to macroscopic quantities such as the size of a disk, the picture described above can predict the radial density profiles of disks. This is interesting since observed disks typically follow an exponential radial profile (at least out to some radius, beyond which the stellar light profile typically truncates - gaseous disks typically extend out further beyond this stellar truncation radius). In a hierarchical Universe, in which dark matter halos and their gas content grow in mass and size with time, the angular momentum of material accreting onto a galaxy will, on average, increase with time also. As a result, disk formation is an "inside out" process, with early infall leading to the formation of the inner regions of the disk and later infall adding primarily to the outer regions. Knowing the distribution of specific angular momenta of the gas from which the disk formed it is possible to determine the distribution of radii at which that gas will settle and, consequently, the radial density profile. Of course, this assumes that the angular momenta of gas elements are unchanged after they arrive in the disk. In reality this may not be the case - viscosity in a gaseous disk may redistribute angular momentum and even in a purely stellar disk stars can scatter from perturbations such as spiral density waves and thereby change their angular momentum and may help to establish the exponential radial profile if the viscous timescale is of order the star formation timescale (Silk and Norman 1981; Lin and Pringle 1987; Clarke 1989, 1991; Firmani et al. 1996). Current results suggest that exponential disks can plausibly arise given our present understanding of the initial distribution of angular momentum, star formation efficiency and supernovae feedback without the need for viscous redistribution of angular momentum (Dutton 2009; Stringer et al. 2010), although the detailed properties (e.g. scale length distributions) of the disks do not necessarily agree perfectly with what is observed (Dutton et al. 2007). Of course, comparison with measurements of stellar disks requires determination of not just the mass density profile but the stellar density profile. Star formation will proceed most rapidly where the gas is densest (i.e. in the inner regions of the disk) and may be inhibited altogether at larger radii where the background radiation can prevent the formation of molecular hydrogen and where the disk may become stable to perturbations and so unable to form molecular cloud complexes (Martin and Kennicutt 2001; Schaye 2004).
The assumption that the angular momentum distribution of the disk remains constant after formation is not precisely correct even in the absence of hydrodynamical effects such as viscosity. Stars in a disk can interact with perturbations such as spiral density waves, exchanging energy and angular momentum with them. Sellwood and Binney (2002) show that interactions between stars and spiral waves at the corotation resonance lead to an exchange of energy and angular momentum that changes the radius of a star's orbit while keeping it circular. A star can, in principle, interact with multiple spiral waves and thereby migrate over a significant radial range. The question of how much radial mixing occurs due to this effect has been examined recently by Roskar et al. (2008a) and Roskar et al. (2008b). They find that this is a significant process which can lead to the formation of a population of stars beyond the star formation truncation radius in a disk, and which also flattens metallicity gradients (particularly in older stellar populations).
Disks are dynamically rather fragile systems and so not only must they form but they must survive across cosmological spans of time. This requires that the disk be stable to the growth of large scale perturbations which could destroy it. Additionally, in a hierarchical universe, survival is a non-trivial feat as the disk must survive frequent merging with other galaxies and constant bombardment by dark matter substructures orbiting within its own dark matter halo. Significant work has gone into studying the effects of dark matter substructures on galactic disks 34 (Toth and Ostriker 1992; Velazquez and White 1999; Font et al. 2001; Benson et al. 2004; Kazantzidis et al. 2008; Read et al. 2008; Kazantzidis et al. 2009; Purcell et al. 2009). The current consensus seems to be that the cold dark matter model is consistent with the presence of thin galactic disks, but only just so, and some fraction of disks have probably been significantly thickened or destroyed by interactions with dark matter substructures.
White and Rees (1978) proposed that galaxies would form as gas cools inside of dark matter halos and demonstrated that this provided a reasonable estimate of the typical mass scale of galaxies. This simple picture has a long standing problem however. The mass function of dark matter halos rises steeply (approximately as M-1.9; Reed et al. 2007) at low masses. Since cooling is very efficient in these low mass halos we might expect the galaxy mass and/or luminosity function to show a similar slope at the low mass/luminosity end. In fact, measured slopes are much shallower (typically around -1; e.g. Cole et al. 2001). Rectifying this discrepancy is usually achieved by postulating some form of feedback, typically from supernovae, which can inhibit star formation in these low mass systems (e.g. by driving a wind out of the galaxy). However, as shown by Benson et al. (2003) this causes another problem - too much gas is now left over to accrete into massive halos (group and cluster mass objects) at late time wherein it cools and forms over-massive galaxies (much more massive than any galaxy observed).
This "overcooling" problem is not easy to solve, for the simple reason that the energy scales involved are much larger than for lower mass systems (the characteristic potential well depth of a dark matter halos scales as M2/3 for halos of the same mean density). Several possible solutions have been proposed however, ranging from thermal conduction (Benson et al. 2003; Dolag et al. 2004; Pope et al. 2005), massive outflows (Benson et al. 2003), multiphase cooling (in which gas cools but is locked up into clouds which are inefficiently transferred to the galaxy; Maller and Bullock 2004, Kaufmann et al. 2009) and feedback from active galactic nuclei.
The AGN feedback scenario has gained considerable favor in the past few years for a variety of reasons. Firstly, observations have indicated that all galaxies seem to contain a central supermassive black hole with a mass that scales roughly in proportion to the mass of the galaxy (Magorrian et al. 1998; Gebhardt et al. 2000a; Ferrarese and Merritt 2000; Gebhardt et al. 2000b; Tremaine et al. 2002). The formation of these black holes must have involved the liberation of large amounts of energy and material sinks deep into the potential well of the black hole in some form of accretion flow (Benson et al. 2003). If this energy can be successfully utilized to counteract the overly rapid cooling of gas onto the galaxy it would provide a natural source of sufficient energy available in every galaxy. Additionally, some feedback loop connection between supermassive black hole and galaxy formation of this type is attractive as it provides a means to explain the correlation between galaxy and black hole properties.
Feedback from AGN can be divided into two categories: quasar mode and radio mode. The quasar mode is triggered when large amounts of gas are funneled into the circumnuclear disk from much larger scales by, for example, a merger between two galaxies in which torques act to transfer angular momentum from the gas, causing it to flow inwards. This is likely the dominant mechanism for black hole mass growth and results in a high (relative to Eddington) accretion rate - most likely through a thin accretion disk - and significant optical luminosity. In contrast, radio mode feedback occurs when the black hole is accreting at a more modest rate due to Bondi accretion from a diffuse hot atmosphere of gas and is in an optically dim but radio loud phase. In this phase, the black hole is thought to drive powerful jets (Meier 1999, 2001; Villiers et al. 2005; Nemmen et al. 2007; Komissarov et al. 2007; Benson and Babul 2009) which can reach to large distances and have been seen to have a significant impact on their surroundings (Birzan et al. 2004). The mechanism via which energy from the jets is efficiently coupled to the hot atmosphere of gas remains poorly understood: a combination of observational evidence (e.g. Owen et al. 2000) and theoretical insights suggest that jets inflate bubbles or cavities in the hot atmosphere (see Section 6.3.2). Despite these uncertainties, semi-analytic treatments which simply assume an efficient coupling have demonstrated that this can effectively shut down cooling in massive halos, resulting in a reduction in the masses of the largest galaxies and good agreement with luminosity functions and the bimodal distribution of galaxy colors (Croton et al. 2006; Bower et al. 2006; Somerville et al. 2008b). Observational evidence in support of AGN feedback is beginning to emerge (Schawinski et al. 2007) and seems to favor a radio mode scenario (Schawinski 2009).
8.4. Local Group Dwarf Satellites
As with any theory, galaxy formation theory is often best tested by exploring its predictions in extremes of physical conditions. For example, while our current theory may do well at explaining the properties of galaxies of average luminosity, it may perform less well in explaining the properties of the lowest mass galaxies that can form. Unfortunately, low mass galaxies are also low luminosity and so are difficult to observe. Fortunately, our own privileged position within the Milky Way and the Local Group means that there exists a population of faint, dwarf galaxies much closer by than we might otherwise expect. Study of the population of Local Group galaxies therefore has the potential to teach us much about galaxy formation at the lowest mass scales (and therefore, in a hierarchical Universe, at the earliest times). We must be cautious, however, of over-interpreting conclusions drawn from the Local Group which is, after all, just one small patch of the Universe.
Until the advent of the Sloan Digital Sky Survey around 11 satellite galaxies were known to exist within the virial radius of the Milky Way's halo 35 (Mateo 1998). The deep and uniform photometry of the SDSS has allowed many new such galaxies to be found by searching for overdensities in the stellar distribution in both position and color (Willman et al. 2005). The current roster of dwarf satellites within the Milky Way's halo amounts to 24 (Tollerud et al. 2008). However, the SDSS covers only around one fifth of the sky and detection algorithms are imperfect. Recent estimates of the total number of dwarf satellites in the Milky Way's halo alone are of the order a few hundred (Tollerud et al. 2008). The faintest galaxy currently known, Segue 1, has a luminosity of only 340 times that of the Sun (Belokurov et al. 2007).
These dwarf galaxies are interesting from a theoretical perspective for several reasons. Firstly, their low mass makes them highly sensitive to feedback effects, both internal (from supernovae for example; Font et al. 2010) and external (photoheating of the IGM by the entire population of galaxies can, in principle, inhibit the formation of these satellites; Gnedin 2000, Okamoto et al. 2008a). Furthermore, they may have gained at least some of their mass as a result of molecular hydrogen cooling, and have very low metallicities which may provide insight into the process of chemical enrichment. Beyond these galaxy-related aspects, the dwarf satellites appear to be highly dark matter dominated (Strigari et al. 2008), making them excellent systems in which to explore the properties of dark matter and, therefore, to place interesting constraints on the behavior of dark matter on small scales.
Consequently, these galaxies have attracted significant theoretical attention over the past few years. In particular, when simulations demonstrated that dark matter substructure could survive within a host halo for significant periods of time, it became clear that the Milky Way's halo should contain thousands of small dark matter halos that could potentially have formed a dwarf galaxy within them (Moore et al. 1999; Kuhlen et al. 2008; Springel et al. 2008). This was in stark contrast to the 10 or so satellites known at that time. This "missing satellites" problem appears to have been largely solved. Theoretical models have demonstrated that a combination of supernovae feedback, suppression of galaxy formation by a photoionizing background and tidal plus ram pressure stripping (Bullock et al. 2000; Somerville 2002; Benson et al. 2002a; Busha et al. 2009; Macció et al. 2009; Wadepuhl and Springel 2010; Font et al. 2010) can reduce the number of satellites significantly (leaving a population of truly dark subhalos; Kormendy and Freeman 2004), while the discovery of new satellites (and accounting for ones as yet undetected) has raised the observational target closer to the theoretical predictions.
Beyond this first order question though, there are many other interesting aspects to the Local Group satellites. For example, while they all contain populations of old stars, many of them show evidence of periodic star formation at much more recent times (Tolstoy et al. 2009). What triggers this star formation? Given that feedback can strongly affect these systems, it is interesting to ask if we can gain insight into the feedback mechanism by studying these galaxies (e.g. their metallicities are highly sensitive to the strength of feedback so may place useful constraints on any feedback model; Font et al. 2010). Finally, some of these galaxies must have been torn apart by the tidal field of the Milky Way (the Sagittarius dwarf is currently suffering this fate) - the dwarf satellite population may therefore have contributed to the build-up of the Milky Way's stellar halo (Cooper et al. 2009), and there may be remnant tidal streams which could provide information about the hierarchical growth of the Milky Way's halo (Bullock and Johnston 2005; Robertson et al. 2005; Font et al. 2006a, b; Johnston et al. 2008).
8.5. The Origins of the Hubble Sequence
The variety of morphologies of galaxies is, perhaps, the most obvious observed characteristic of galaxies. Traditionally, morphology has been measured "by eye" by a trained observer who classifies each galaxy into a different morphological class based upon (amongst other things) the prominence of any central bulge, how concentrated the light distribution is and the presence or otherwise of dust lanes. Hubble (1936; see also de Vaucouleurs 1959) placed galaxies into a morphological classification scheme using such an approach, and this basic morphological classification has persisted to the present (de Vaucouleurs et al. 1991). Applying this type of morphological classification to today's large datasets is difficult, but has been achieved by utilizing "crowdsourcing" techniques (Lintott et al. 2008). A key observational goal is to assess how the Hubble sequence evolves over time, as this should place strong constraints on theoretical models. This is observationally challenging, but progress is being made (e.g. Kriek et al. 2009).
Theoretically, morphological evolution is inevitable in a hierarchical universe in which galaxies interact with each other. Early work demonstrated that major mergers between galaxies could transform disks into spheroids leading to morphological evolution (Barnes and Hernquist 1992), but it is clear that the picture is more complicated, with secular evolution playing an important role in transforming disks into spheroids (Kormendy and Kennicutt 2004) and major mergers of very gas rich systems can lead to the reformation of a disk after the merger is over (Barnes 2002; Springel and Hernquist 2005; Robertson et al. 2006a).
A fundamental difficulty in assessing the ability of any given theoretical model to explain the morphological properties of galaxies is that the definition of morphology itself is very complicated, and somewhat nebulously defined. This problem is beginning to be circumvented, both by the ability of numerical simulations of galaxy formation to produce realistic "mock images" of galaxies (Jonsson 2006) which can, in principle, be classified by eye just as a real galaxy, and by the use of more quantitative morphological measures such as bulge-disk decomposition (Schade et al. 1996, Ratnatunga et al. 1999, Simard et al. 2002, Benson et al. 2007), Gini-M20 (Lotz et al. 2004), concentration-asymmetry-smoothness (Watanabe et al. 1985, Abraham et al. 1996, Bell et al. 2003) and so on.
Understanding the build-up and evolution of the Hubble sequence of morphologies is, nevertheless, an important task for galaxy formation theory. The morphological structure of a galaxy clearly tells us something about its formation history and therefore captures information which its stellar population, for example, does not. Several studies have explored this aspect of galaxy formation theory (Baugh et al. 1996a, b; Kauffmann 1996; Governato et al. 1999; Firmani and Avila-Reese 2003; Lucia et al. 2006; Lucia and Blaizot 2007; Governato et al. 2007; Parry et al. 2009; Benson and Devereux 2009) with the general conclusion that hierarchical cosmologies can plausibly give rise to the observed mix of morphological types, although with significant uncertainties remaining in both the modeling of morphological transformation and in the comparison with observed morphologies. The consensus opinion is that massive elliptical galaxies form most of their stars in smaller progenitor galaxies and only assemble them into a single galaxy significantly later, while spiral galaxies are dominated by in situ star formation. Secular evolution of disks into spheroids also seems to be a crucial ingredient, particularly in the production of lower mass spheroidal systems (Parry et al. 2009; Kormendy et al. 2009).
33 It is conserved if we ignore the possibility of torques between baryons and dark matter which could transfer angular momentum from the gas to the dark halo. We will review this assumption later. Back.
34 Primarily because this is potentially a means by which to rule our the cold dark matter scenario: if the predicted abundance of substructure was sufficient to destroy galactic disks, the model could be ruled out. Back.
35 We are following the definition of virial radius given by Benson et al. (2002a) here. Under this definition, 9 Local Group satellites are within the virial radius of M31, while a further 19 lie outside of the virial radii of the halos of both the Milky Way and M31. Back.